洛谷P4568题解
hdu3499题解
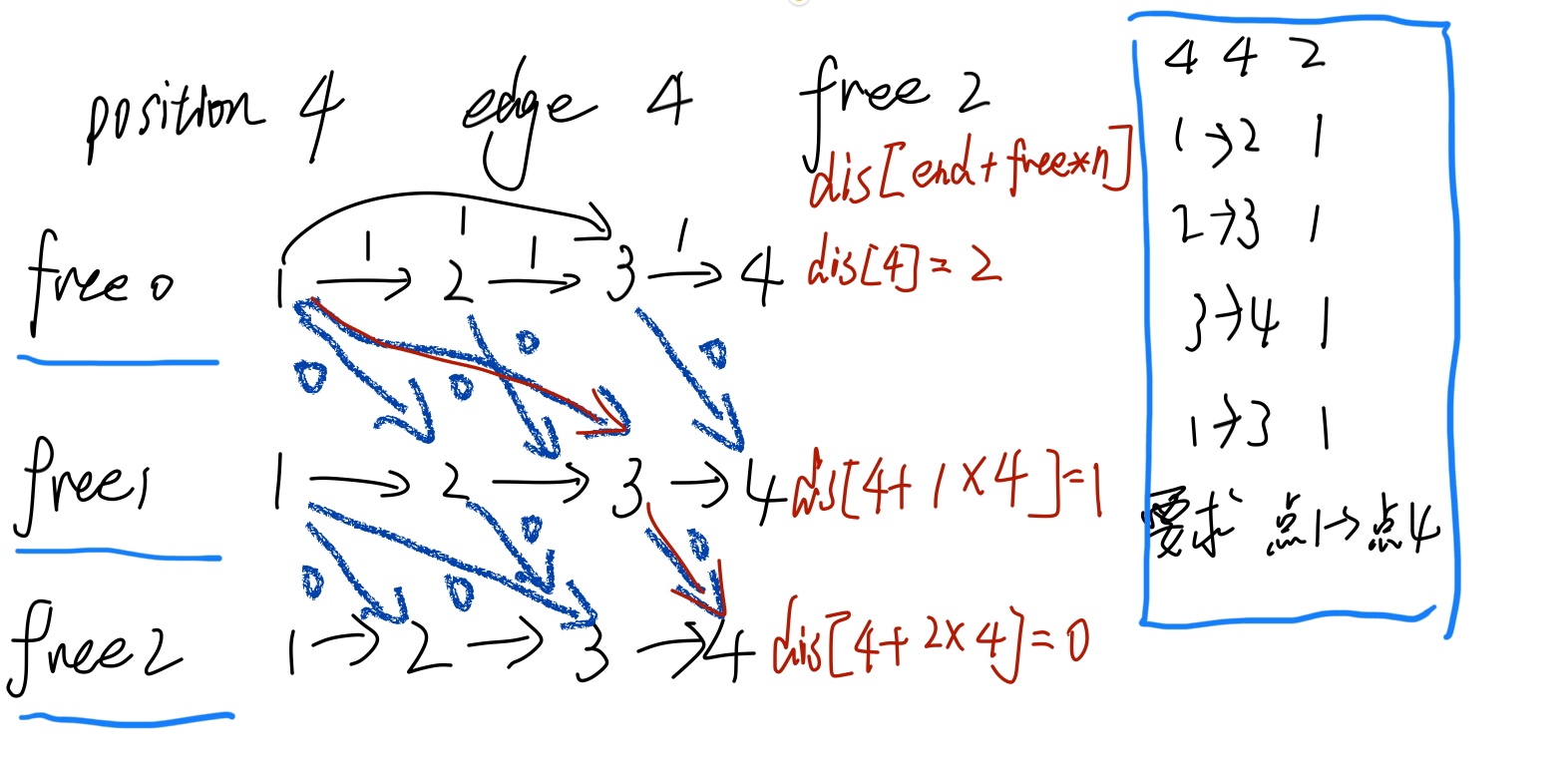
用一张图解释
就是把free的路线进行分层计算到这个点的距离最小是多少,假设点为pos
mindis=min(mindis,dis[pos+i*n]);0<=i<=free n是多少个点
题意:
在一个带权无向图,n个点,m条边,k个权力(使得一条边权变成0)
再给起始位和终点位,给m条边的u,v,w的信息,求最少路费
思路:
m小于等于50000,k小于等于10,链式前向星的话需要2*2*(10+1)(双向*建零边和带权边(k+1层))
因为当i==k的时候,权力是0,所以不用建第k层的零边的
用dijkstra跑就行了

1 #include<bits/stdc++.h>
2 using namespace std;
3 #define ll long long
4 #define il inline
5 #define it register int
6 #define inf 0x3f3f3f3f
7 #define lowbit(x) (x)&(-x)
8 #define pii pair<int,int>
9 #define mak(n,m) make_pair(n,m)
10 #define mem(a,b) memset(a,b,sizeof(a))
11 #define mod 998244353
12 const int maxn=5e4*44;
13 int n,m,k,tot,s,t;
14 int head[maxn],dis[maxn],vis[maxn];
15 struct node{int to,w,next;}edge[maxn];
16 il void add(int u,int v,int w){
17 edge[tot].to=v;edge[tot].w=w;
18 edge[tot].next=head[u];head[u]=tot++;
19 }
20 il void dijkstra(){
21 priority_queue<pii,vector<pii>,greater<pii> >q;
22 dis[s]=0;q.push({dis[s],s});//q.push(mak(dis[s],s));
23 while(!q.empty()){
24 int now=q.top().second;
25 q.pop();
26 if(vis[now])continue;vis[now]=1;
27 for(it i=head[now];~i;i=edge[i].next){
28 int v=edge[i].to;
29 if(!vis[v] && dis[v]>dis[now]+edge[i].w){
30 dis[v]=dis[now]+edge[i].w;
31 q.push({dis[v],v});
32 }
33 }
34 }
35 }
36 int main(){
37 while(~scanf("%d%d%d",&n,&m,&k)){
38 scanf("%d%d",&s,&t);
39 for(it i=0;i<maxn;i++){
40 head[i]=-1;dis[i]=inf;vis[i]=0;
41 }tot=0;
42 for(it i=0;i<m;i++){
43 int u,v,w;
44 scanf("%d%d%d",&u,&v,&w);
45 for(it i=0;i<=k;i++){
46 add(u+i*n,v+i*n,w);
47 add(v+i*n,u+i*n,w);
48 if(i!=k){
49 add(u+i*n,v+(i+1)*n,0);
50 add(v+i*n,u+(i+1)*n,0);
51 }
52 }
53 }
54 dijkstra();int ans=inf;
55 for(it i=0;i<=k;i++){
56 ans=min(ans,dis[t+i*n]);
57 }
58 printf("%d\n",ans);
59 }
60 return 0;
61 }
题意:
在一个带权无向图,n个点,m条边
给m条边的u,v,w的信息,可以有一个权力使得一条边的路费减半
再给起始位和终点位,求最少路费
思路:
分两层最短路,因为是很早之前的代码,贼青涩……

1 #include<iostream>
2 #include<cstdio>
3 #include<cstring>
4 #include<algorithm>
5 #include<map>
6 #include<string>
7 #include<vector>
8 #include<queue>
9 #include<functional>
10 #pragma warning(disable:4996)
11 using namespace std;
12 const int maxn = 200010;
13 #define inf 0x3f3f3f3f3f3f3f
14 #define mem(k,b) memset(k,b,sizeof(k))
15 #define pi pair<int,int>
16 #define mak(n,m) make_pair(n,m)
17 #define ll long long
18 vector<pi> g[maxn];
19 ll a[maxn];
20 bool vis[maxn];
21 map<string, int>mp;
22 int i, j, k, n, l, m, s, t, w;
23 string p, q;
24 struct cmp2 {
25 bool operator()(const pi a,const pi b){
26 return a.second > b.second;
27 }
28 };
29 /*struct cmp2{
30 friend bool operator<(const pi a, const pi b){
31 return a.second > b.second;
32 }
33 };*/
34 inline void di(int s){
35 priority_queue<pi, vector<pi>, cmp2 >q;
36 a[s] = 0;
37 q.push(mak(s, 0));
38 while (!q.empty())
39 {
40 pi tmp = q.top(); q.pop();
41 int u = tmp.first;
42 if (vis[u]){
43 continue;
44 }
45 vis[u] = true;
46 for (int i = 0; i < g[u].size(); i++)
47 {
48 int v = g[u][i].first;
49 int w = g[u][i].second;
50 if (a[v] > a[u] + w)
51 {
52 a[v] = a[u] + w;
53 q.push(mak(v, a[v]));
54 }
55 }
56 }
57 }
58 int main()
59 {
60 while (~scanf("%d%d", &n, &m)){
61 int nn = n << 1;
62 for (int i = 0; i <= nn; i++){
63 g[i].clear();
64 a[i] = inf;
65 vis[i] = false;
66 }
67 mp.clear();
68 int t1 = 1;
69 for (int i = 0; i < m; i++){
70 cin >> q >> p;
71 scanf("%d", &t);
72 if (mp[p] == 0){
73 mp[p] = t1;
74 t1++;
75 }
76 if (mp[q] == 0){
77 mp[q] = t1;
78 t1++;
79 }
80 g[mp[q]].push_back(mak(mp[p], t));
81 g[mp[q]].push_back(mak(mp[p] + n, t / 2));
82 g[mp[q] + n].push_back(mak(mp[p] + n, t));
83 }
84 cin >> q >> p;
85 if (mp[p] == 0){
86 mp[p] = t1++;
87 }
88 if (mp[q] == 0){
89 mp[q] = t1++;
90 }
91 int kai = mp[q], jie = mp[p];
92 di(kai);
93 ll ans = (a[jie], a[jie + n]);
94 if (ans == inf){
95 printf("-1\n");
96 }
97 else{
98 printf("%lld\n", ans);
99 }
100 }
101 return 0;
102 }
模板 返回顶部

1 #define ll long long
2 #define il inline
3 #define it register int
4 #define inf 0x3f3f3f3f
5 #define lowbit(x) (x)&(-x)
6 #define pii pair<int,int>
7 #define mak(n,m) make_pair(n,m)
8 #define mem(a,b) memset(a,b,sizeof(a))
9 #define mod 998244353
10
11 int n,m,k,tot,s,t;
12 int head[maxn],dis[maxn],vis[maxn];
13 struct node{int to,w,next;}edge[maxn];
14
15 il void add(int u,int v,int w){
16 edge[tot].to=v;edge[tot].w=w;
17 edge[tot].next=head[u];head[u]=tot++;
18 }
19
20
21 il void dijkstra(){
22 priority_queue<pii,vector<pii>,greater<pii> >q;
23 dis[s]=0;q.push({dis[s],s});//q.push(mak(dis[s],s));
24 while(!q.empty()){
25 int now=q.top().second;
26 q.pop();
27 if(vis[now])continue;vis[now]=1;
28 for(it i=head[now];~i;i=edge[i].next){
29 int v=edge[i].to;
30 if(!vis[v] && dis[v]>dis[now]+edge[i].w){
31 dis[v]=dis[now]+edge[i].w;
32 q.push({dis[v],v});
33 }
34 }
35 }
36 }
37
38 scanf("%d%d%d",&u,&v,&w);
39 for(it i=0;i<=k;i++){
40 add(u+i*n,v+i*n,w);
41 add(v+i*n,u+i*n,w);
42 if(i!=k){
43 add(u+i*n,v+(i+1)*n,0);
44 add(v+i*n,u+(i+1)*n,0);
45 }
46 }
来源:https://www.cnblogs.com/luoyugongxi/p/12442978.html
