6-DoF相关基础知识整理

刚刚接触这个领域，因此打算花点时间先整理一下相关的一些基础的知识。
首先是第一个概念

一、什么是6-DoF,即6个自由度是什么？

首先，先解释一下自由度，自由度与刚体在空间中的运动相关。可以理解为物体移动的不同基本方式。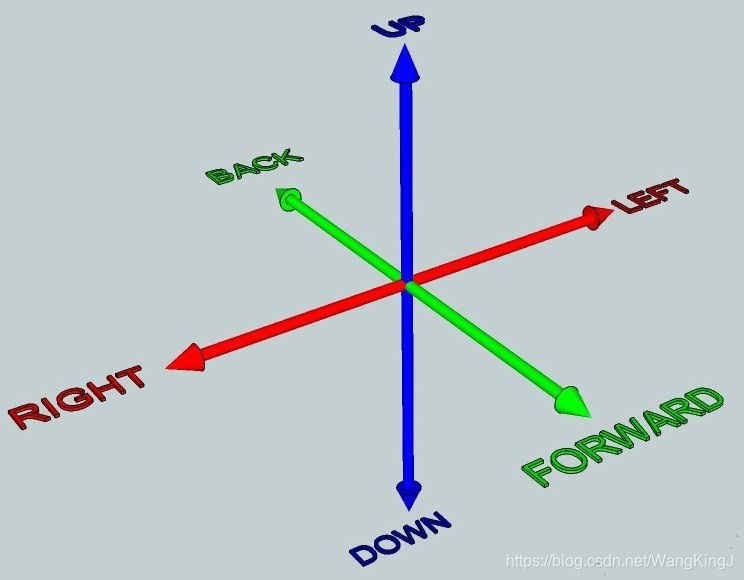
在这里插入图片描述
自由度一共有6个，可以分为两种类型：平移和旋转。

1. 平移运动

刚体可以在3个自由度中平移：向前/后，向上/下，向左/右

2. 旋转运动

刚体在3个自由度中旋转：纵摇(Pitch)、横摇(Roll)、垂摇(Yaw)

因此，3种类型的平移自由度+3种类型的旋转自由度 = 6自由度

在任意一个自由度中，物体可以沿两个“方向”自由运动。例如，电梯限制在1个自由度中(垂直平移)，但电梯能够在这个自由度中上下运动。同样，摩天轮限制在1个自由度中，但这是旋转自由度，所以摩天轮能够朝相反的方向旋转。
我们可以继续举例子，比如说主题公园。碰碰车总共有3个自由度：它只能在3轴中的2条里平移(无法像电梯那样上下移动);然后它只能以一种方式旋转(无法像飞机那样纵摇和垂摇)。所以2个平移+1个旋转=3自由度。
无论有多复杂，刚体的任何可能性运动都可以通过6自由度的组合进行表达。例如在你用球拍击打网球的时候，球拍的复杂运动可以表示为平移和旋转的组合。

二、PnP算法

1. PnP算法是什么？

PnP(Perspective-n-Point)是求解 3D 到 2D 点对运动的方法。它描述了当我们知道n 个 3D 空间点以及它们的投影位置时,如何估计相机所在的位姿。——《视觉SLAM十四讲》

通俗的讲，PnP问题就是在已知世界坐标系下N个空间点的真实坐标以及这些空间点在图像上的投影，如何计算相机所在的位姿。换句话说，就是已知量为空间中的真实坐标和图像坐标，求解相机的位姿（未知量）

2. PnP问题的求解方法

PnP问题是在已知n 个 3D 空间点以及它们的投影位置时估计相机所在的位姿。那么 n 最小为多少时我们才能进行估算呢（最少需要几个3D-2D点对）？
我们可以设想以下场景，设相机位于点Oc，P1、P2、P3……为特征点。

场景1：N = 1时
当只有一个特征点P1，我们假设它就在图像的正中央，那么显然向量OcP1就是相机坐标系中的Z轴，此时相机永远是面对P1，于是相机可能的位置就是在以P1为球心的球面上，此外球的半径也无法确定，于是有无数个解。

场景2：N = 2时
现在多了一个约束条件，显然OcP1P2形成一个三角形，由于P1、P2两点位置确定，三角形的边P1P2确定。再加上向量OcP1和OcP2，从Oc点射向特征点的方向角也能确定。于是能够计算出OcP1的长度=r1，OcP2的长度=r2。于是这种情况下得到两个球：以P1为球心，半径为r1的球A；以P2为球心，半径为r2的球B。显然，相机位于球A，球B的相交处，依旧是无数个解。

场景3：N = 3时
这次又多了一个以P3为球心的球C，相机这次位于ABC三个球面的相交处，终于不再是无数个解了，这次应该会有4个解，其中一个就是我们需要的真解——即相机真实的位姿。

场景4：N > 3时
N=3时求出4组解，好像再加一个点就能解决这个问题了，事实上也几乎如此。说几乎是因为还有其他一些特殊情况，这些特殊情况就不再讨论了。N>3后，能够求出正解了，但为了一个正解就又要多加一个球D显然不够"环保"，为了更快更节省计算机资源地解决问题，先用3个点计算出4组解获得四个旋转矩阵、平移矩阵。根据公式：
在这里插入图片描述
将第四个点的世界坐标代入公式，获得其在图像中的四个投影（一个解对应一个投影），取出其中投影误差最小的那个解，就是我们所需要的正解。

PnP算法的推导看
算法推导及详细讲解

三、什么是姿态？

姿态是用来描述两个坐标系之间相对关系的。一个点相对于一个坐标系没办法定义姿态，相反，一个坐标系相对一个点也没法定义姿态，所以，姿态必须是两个坐标系之间的事情。目前有四种流行的姿态表示法，它们是欧拉角、旋转矩阵、四元数和旋转矢量。四元数和旋转矩阵具有一定的相似性，旋转矢量的运算很难使用，下面主要讲述欧拉角和旋转矩阵。

3.1 欧拉角和旋转矩阵

欧拉角表示为三个角度（容易被人们直观接受，因此很有欺骗性），意义是：如果我们要表示两个坐标系之间的关系，那么就将一个坐标系分别沿某些坐标系旋转相应的角度，就能和另一坐标系重合。因此欧拉角就具有了两个属性：旋转轴顺序，和旋转角度。

3.1.1 欧拉角

拿我们最常见的滚转 $\phi$ 、俯仰 $\theta$ 、偏航 $\psi$ 来说，它们的含义是：从W系出发，首先绕Z轴旋转 $\psi$ ，然后绕Y轴旋转 $\theta$ ，最后沿X轴旋转 $\phi$ ，就和B系重合了；将这样的旋转顺序称为（从静止坐标系到动坐标系的）Z-Y-X。因此，我们在文献里看到滚转、俯仰、偏航的时候，还要注意旋转顺序，比如UPenn著名的V. Kumar教授团队，就比较喜欢使用Z-X-Y顺序。
对两个坐标系而言，不同的旋转顺序会导致大小不同的欧拉角，但也不用太费解，因为它们虽然有不同的旋转顺序、不同的欧拉角大小，不同的旋转矩阵计算公式等等，但两个坐标系之间的关系就在那里，就像我们前面说的那样，不论我们怎么描述，它们的相对关系本身是不会变的。而且，不论使用什么欧拉角旋转顺序，最终得到的旋转矩阵在数值上一定是相同的——因为描述的是同一个关系嘛！所以，这就是使用旋转矩阵的巨大优点：明确。（然而，还是有许多小伙伴被B转W，W转B搞得头晕脑胀，这个稍后再聊）

3.1.2 旋转矩阵

旋转矩阵（rotation matrix），又称方向余弦矩阵（Direction Cosine Matrix，DCM），同时也是SO(3)群的元素。作用就是把某个向量在一个坐标系的投影转换到另一个坐标系去，这里用 $C_B^W$ 表示旋转矩阵（还有用 $R_B^W$ 的，也很直观），下标是原始坐标系，上标是目标坐标系，这里放一张图吧。
在这里插入图片描述
注意，还是那句话，向量是客观存在的！旋转矩阵变换的只是表示向量的坐标系。

3.1.3对旋转矩阵的理解

看图说话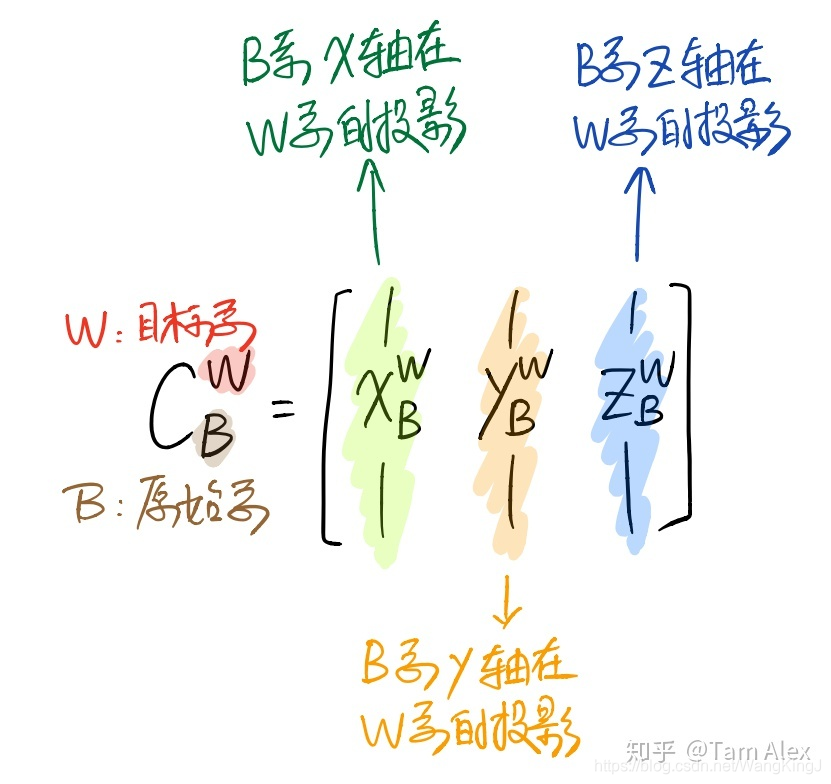
在这里插入图片描述
也就是说，旋转矩阵的第1、2、3列，实际上是原始坐标系的x、y、z轴，在目标坐标系里的投影。比如原始坐标系和目标坐标系重合时，x轴是 $[1,0,0]^T$ ,y轴是 $[0,1,0]^T$ ,z轴是 $[0,0,1]^T$ ,用它们组成旋转矩阵的1、2、3列，就是单位矩阵，也就是说向量在原始坐标系和在目标坐标系的投影是一样的。反过来， $C_W^B$ 的各列就是W系各坐标轴在B系中的投影，按照这种理解方式，会得到许多有趣的视角，下面就来看看怎么用这种理解方式来推导绕单轴的旋转矩阵。

3.1.4 绕单轴的旋转矩阵

对于绕单轴的旋转矩阵，很多小伙伴分不清楚到底是B转W还是W转B的，下面就先用上面对旋转矩阵的理解来推导一下绕单轴的旋转矩阵，然后介绍下怎么记忆。注意对旋转正负号的定义，惯用的定义是，从原点沿着坐标轴看，顺时针为正。下面看图。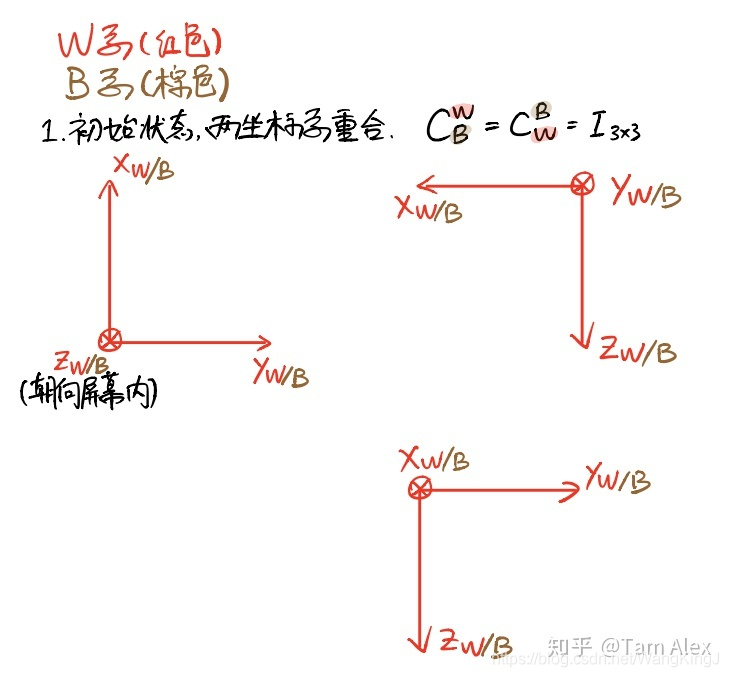
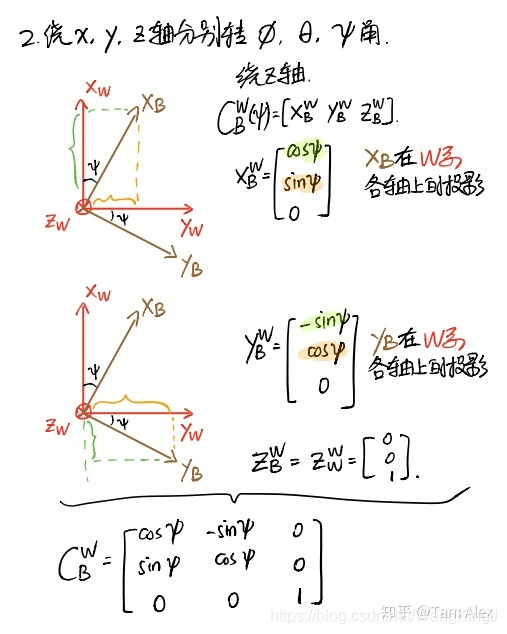
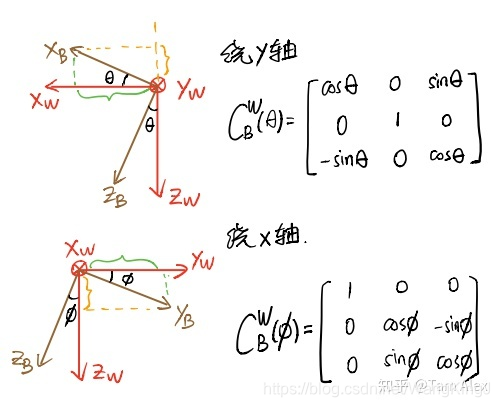
在这里插入图片描述

初始状态的W和B系

在这里插入图片描述

绕Z轴旋转

在这里插入图片描述

绕Y、X轴旋转

这样就通过计算B系各坐标轴在W系的投影得到了绕各轴旋转的 $C_B^W$ ,反之计算W系在B系的投影就可得到绕各轴旋转的 $C_W^B$ 不过因为它们互为转置，所以得到了一个，就知道另一个了。注意这里的W系和B系可以换成任意两个坐标系，只要把握哪个坐标系是动坐标系，以及我们要找哪个坐标系到哪个坐标系的旋转矩阵就不容易出错了。绕单轴的旋转矩阵对角线都是余弦或1，其他的0元素也很容易确定，讨厌的就是正弦函数前面的正负号了。那么我的记忆方法就是。。。还是把旋转的两个轴画出来，然后只要确定一个正弦的符号，另一个位置的正弦取相反的符号就行了。确实还是挺麻烦，不过按照这个理解是不会搞错B转W和W转B的，大家可以试一试。
我们把绕x、y、z的从B系到W系的单轴旋转矩阵分别 $C_B^W(\phi)，C_B^W(\theta)、C_B^W(\psi)$ ,那么就有 $C_B^W=C_B^W(\phi)C_B^W(\theta)C_B^W(\psi)$ ,正好对应了从B系到W系的旋转顺序。这也叫链式法则。