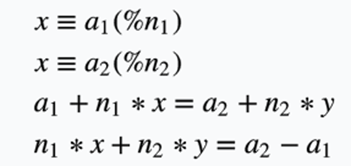1. 一条数学公式：如果有 a%b=c, 则有 (a+kb)%b=c(k 为非零整数)
2. 用途：求解一次线性同余方程组
，需要将模数转化为素数来求解的题目
3. (N/mi)yi≡1(modmiyi(N/m1)+qm1=1 （若mi互质，1=gcd(N/m1,m1)）
//hoho，前面一大堆乱七八糟的困得时候写的，重新来
前提：mi两两互质 --》可推出任意ai方程组都有解
假设：
求解：所以方程组的通解形式为 x=a1t1M1+a2t2M2+...+antnMn+kM, k∈Z
在模M的意义下，方程组只有一个解 x=(a1t1M1+a2t2M2+...+antnMn）mod M
①求基础数的方法：(1) while自增，用其他数的最小公倍数不断自增，直到余数满足条件
(2) 辗转相除法，联系乘法逆元。
证明：
j
除此之外，参考百科（真的看不懂了orz
▲联系孙子算法的那题，就是：已知m1,m2,m3是两两互质的正整数，求最小的正整数x，使它被m1,m2,m3除所得的余数分别是c1,c2,c3。
(1) 先求出Mi 即不被mi整除，但被其他两个数整除的数
(3) 这么搞则得到满足题意的数c1M1+c2M2+c3M3，但它不一定最小，如果比lcm小的话减一下就好。
tips：①定理：两个数相加，如果一个能被a整除，一个不能，那么它们的和，就不能被整数a整除。然后根据这条定理，步骤(3)即可证，为了得到最小，用最小公倍数（因为最小公倍数是能同时被所有数整除的最小数，运用定理，减去后还是满足条件（加或减看两者大小）
②基础数可能为负
4. 扩展CRT： m1,m2,m3..不一定互质
