HDU - 4507 吉哥系列故事——恨7不成妻（思维数学+结构体上的数位dp）

题目链接：https://vjudge.net/contest/347034#problem/I

Problem Description 　　
单身！依然单身！吉哥依然单身！
　　DS级码农吉哥依然单身！
　　所以，他生平最恨情人节，不管是214还是77，他都讨厌！
　　吉哥观察了214和77这两个数，发现：
　　2+1+4=7
　　7+7=72
　　77=711
　　最终，他发现原来这一切归根到底都是因为和7有关！所以，他现在甚至讨厌一切和7有关的数！什么样的数和7有关呢？
　　如果一个整数符合下面3个条件之一，那么我们就说这个整数和7有关——
　　1、整数中某一位是7；
　　2、整数的每一位加起来的和是7的整数倍；
　　3、这个整数是7的整数倍；
　　现在问题来了：吉哥想知道在一定区间内和7无关的数字的平方和。

Input
输入数据的第一行是case数T(1 <= T <= 50)，然后接下来的T行表示T个case;每个case在一行内包含两个正整数L, R(1 <= L <= R <= 10^18)。

Output
请计算[L,R]中和7无关的数字的平方和，并将结果对10^9 + 7 求模后输出。

Sample Input

Sample Output

236
221
0

分析：
数位dp的功能：能求出一段区间内满足条件的个数
题目要求：一段区间内满足条件的数的平方和
借助第三个变量：一段区间内满足条件的数的总和，利用结构体+数位dp将三个联系起来

三维dp表示的结构体

struct node
{
    LL cnt;/*满足条件的个数*/
    LL sum1,sum2;/*一次方和,二次方和*/
} dp[20][10][10];

利用数位dp的逐位遍历的本质性，将三者联系起来

dfs最初传入的是 dfs(tot,0,0,1)
与之相对应的是 dfs(int pos,int sum,int num,int limt)
sum：每一位的和—>(sum+i)%7
num：这个数本身—>(num*10+i)%7
当前位为pos，填入i，递归开始遍历下一位
cnt：当前位为i，后面全部都满足条件的数的个数
res为当前位pos的状态，temp为下一位pos-1的状态

res.sum1=cnt * i *10 ^ (pos-1)+temp.sum1
res时这个数是pos位，temp时这个数是pos-1位，res比temp多了一位，对应多的这一位对sum1的贡献为 i * 10 ^(pos-1) *cnt

考虑sum2，即符合条件数的平方和。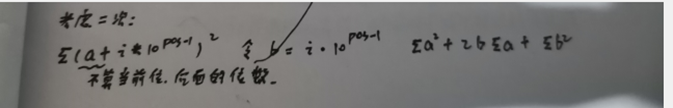
在这里插入图片描述
涉及的累加是乘以对应符合条件的个数

代码：

#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
typedef long long LL;
const int mod=1e9+7;
LL p[20];
int tot,a[20];
struct node
{
    LL cnt;/*满足条件的个数*/
    LL sum1,sum2;/*一次方和,二次方和*/
} dp[20][10][10];
node dfs(int pos,int sum,int num,int limt)
{
    if(pos==0)
    {
        node w;
        w.sum1=0,w.sum2=0;
        w.cnt=(sum&&num);/*sum和num有一个为0，就表示能被7整除,不符合情况*/
        return w;
    }
    if(!limt&&dp[pos][sum][num].cnt!=-1)
        return dp[pos][sum][num];
    int up=limt?a[pos]:9;
    node res;
    res.cnt=0,res.sum1=0,res.sum2=0;
    for(int i=0; i<=up; i++)
    {
        if(i==7)
            continue;
        node temp=dfs(pos-1,(sum+i)%7,(num*10+i)%7,limt&&(i==up));/*temp表示的相当于子位的情况*/
        res.cnt=(res.cnt+temp.cnt)%mod;
        LL s=(i*p[pos-1])%mod;
        res.sum1=(res.sum1+(s*temp.cnt)%mod+temp.sum1)%mod;
        LL t=(2*s)%mod;
        res.sum2=(res.sum2+(((s*s)%mod)*temp.cnt)%mod+(t*temp.sum1)%mod+temp.sum2)%mod;
    }
    if(!limt)
        return dp[pos][sum][num]=res;
    return res;
}
LL solve(LL n)
{
    int tot=0;
    while(n)
    {
        a[++tot]=n%10;
        n/=10;
    }
    node ans=dfs(tot,0,0,1);
    return ans.sum2;
}
void init()
{
    p[0]=1;
    for(int i=1; i<=18; i++)
        p[i]=(p[i-1]*10)%mod;
    for(int i=0; i<20; i++)
        for(int j=0; j<10; j++)
            for(int k=0; k<10; k++)
                dp[i][j][k].cnt=-1;
}
int main()
{
    int T;
    scanf("%d",&T);
    init();
    while(T--)
    {
        LL x,y;
        scanf("%lld%lld",&x,&y);
        printf("%lld\n",(solve(y)-solve(x-1)+mod)%mod);
    }
    return 0;
}

来源：CSDN

作者：zaiyang遇见

链接：https://blog.csdn.net/lylzsx20172018/article/details/104266408

标签

num