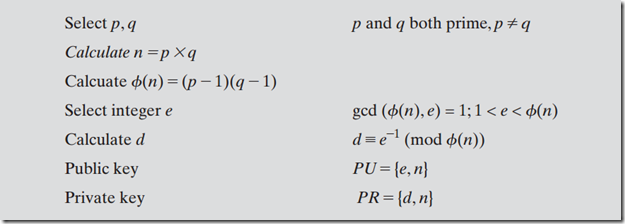RSA是一种非对称加密算法,在公开密钥和电子商业中RSA被广泛使用。它是基于一个很简单的数论事实,两个素数相乘很容易,对两素数乘积因式分解很困难。原理就不再阐述了,我谈谈算法的编程实现过程。
一、RSA加密和解密过程是基于以下形式,其中明文为M,密文为C,公匙PU={e, n},密匙PR={d, n}。
1、准备工作,选择两个大素数p和q,计算p和q的乘积n,计算p-1和q-1的乘积,选择一个与p-1和q-1乘积互质的数e,计算出d
2、加密过程
3、解密过程
程序没有生成大素数,只是列出1000以内的素数,随机取两个素数p和q,利用欧德里德扩展算法计算出e和d,用反复平方法求数的幂
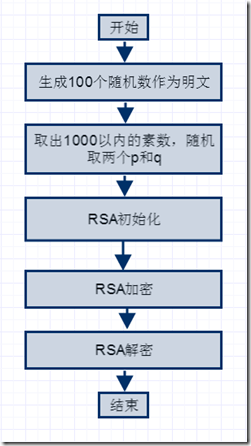
二、程序流程图
三、程序源码
#include <iostream>
#include <cmath>
#include <cstring>
#include <ctime>
#include <cstdlib>
using namespace std;
int Plaintext[100];//明文
long long Ciphertext[100];//密文
int n, e = 0, d;
//二进制转换
int BianaryTransform(int num, int bin_num[])
{
}
//反复平方求幂
long long Modular_Exonentiation(long long a, int b, int n)
{
}
//生成1000以内素数
int ProducePrimeNumber(int prime[])
{
}
//欧几里得扩展算法
int Exgcd(int m,int n,int &x)
{
}
//RSA初始化
void RSA_Initialize()
{
}
//RSA加密
void RSA_Encrypt()
{
}
//RSA解密
void RSA_Decrypt()
{
}
//算法初始化
void Initialize()
{
}
int main()
{
}
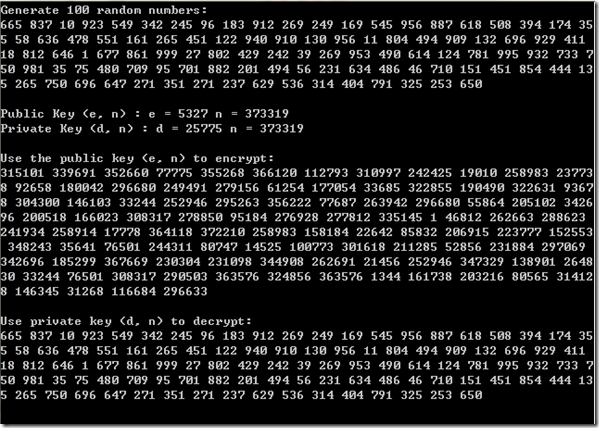
四、运行结果