Peterson's algorithmconcurrent programmingalgorithmmutual exclusionGary L. Peterson[1][2]
The algorithm
flagturnflag[n]truencritical sectionturn
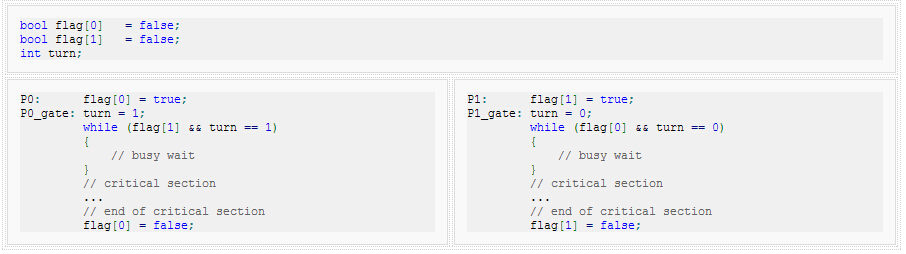
turnflag[0]flag[1][1]
The three criteria are mutual exclusion, progress, and bounded waiting.[3]
Mutual exclusion
P0 and P1 can never be in the critical section at the same time: If P0 is in its critical section, then flag[0] is true. In addition, either flag[1] is false (meaning P1 has left its critical section), or turn is 0 (meaning P1 is just now trying to enter the critical section, but graciously waiting), or P1 is at label P1_gate (trying to enter its critical section, after setting flag[1] to true but before setting turn to 0 and busy waiting). So if both processes are in their critical sections then we conclude that the state must satisfy flag[0] and flag[1] and turn = 0 and turn = 1. No state can satisfy both turn = 0 and turn = 1, so there can be no state where both processes are in their critical sections. (This recounts an argument that is made rigorous in.[4])
Progress
Progress is defined as the following: if no process is executing in its critical section and some processes wish to enter their critical sections, then only those processes that are not executing in their remainder sections can participate in making the decision as to which process will enter its critical section next. This selection cannot be postponed indefinitely.[3]
Bounded waiting
Bounded waiting means that "there exists a bound or limit on the number of times that other processes are allowed to enter their critical sections after a process has made a request to enter its critical section and before that request is granted".[3]
Filter algorithm: Peterson's algorithm for N processes
The filter algorithm generalizes Peterson's algorithm for N processes. It uses N different levels - each represents another 'waiting room', before the critical section. Each level will allow at least one process to advance, while keeping one process in waiting.
// initialization level[N] = { -1 }; // current level of processes 0...N-1 waiting[N-1] = { -1 }; // the waiting process of each level 0...N-2 // code for process #i for(l = 0; l < N-1; ++l) { level[i] = l; waiting[l] = i; while(waiting[l] == i && (there exists k ≠ i, such that level[k] ≥ l)) { // busy wait } } // critical section level[i] = -1; // exit sectionNote
test-and-setcompare-and-swapSMP
memory orderingmemory barrierPowerPCXbox 360).
atomic operationx86load-link/store-conditionalAlphaMIPSPowerPC, and other architectures. These instructions are intended to provide a way to build synchronization primitives more efficiently than can be done with pure shared memory approaches.