1. 几个景点算法:
1. 修路问题:最小生成树(加权值)+ 普利姆
2. 最短路径:图+弗洛伊德算法
3. 汉诺塔: 分支的算法
4. 八皇后:回朔法、
5. 丢手帕 : 约瑟夫问题
2. 线性结构 与非线性结构
1.线性结构 :数据元素之间存在一对一的线性关系
顺序存储结构 , 链式存储结构
(数组,队列,链表和栈)
2 . 非线性结构:(二维数组,多维数组,广义表,树结构,图结构)
3. 稀疏数组
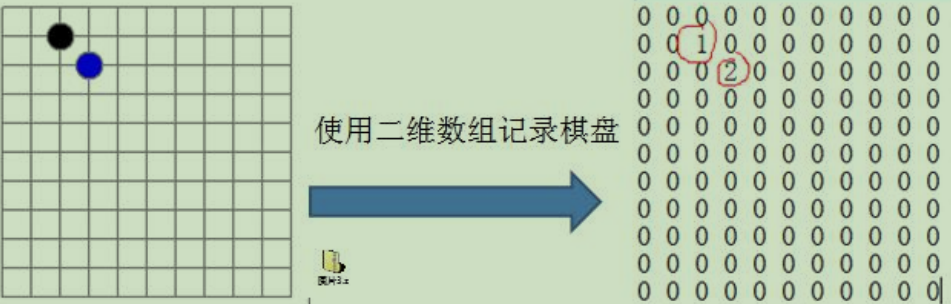
因为该数组中记录了很多值是默认值0,记录了很多没有意义的数据 -》 稀疏数组

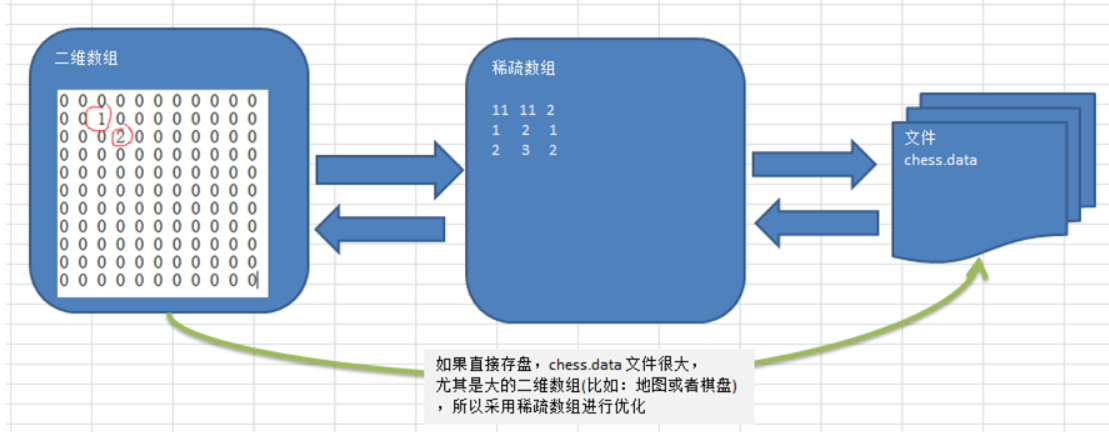
代码实现
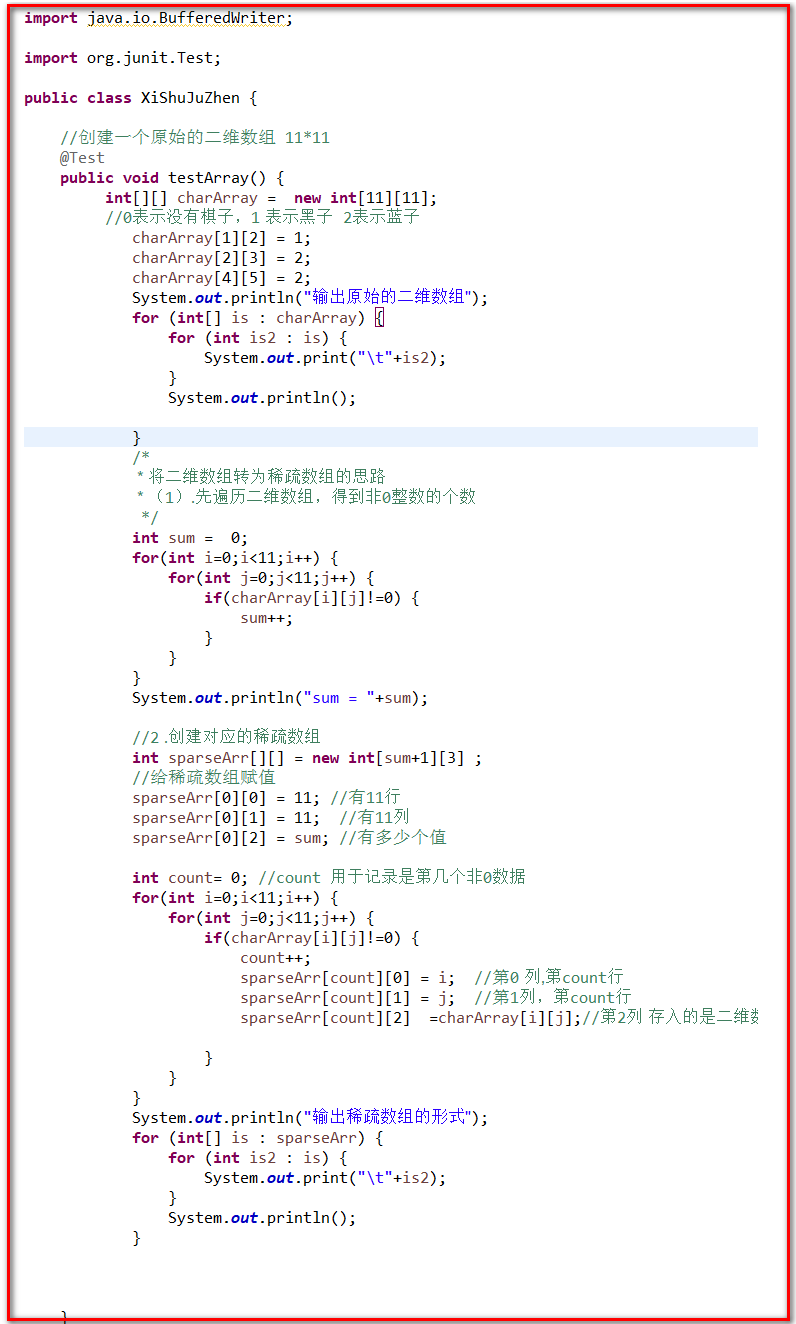

public class XiShuJuZhen {
//创建一个原始的二维数组 11*11
@Test
public void testArray() {
int[][] charArray = new int[11][11];
//0表示没有棋子,1 表示黑子 2表示蓝子
charArray[1][2] = 1;
charArray[2][3] = 2;
charArray[4][5] = 2;
System.out.println("输出原始的二维数组");
for (int[] is : charArray) {
for (int is2 : is) {
System.out.print("\t"+is2);
}
System.out.println();
}
/*
* 将二维数组转为稀疏数组的思路
* (1).先遍历二维数组,得到非0整数的个数
*/
int sum = 0;
for(int i=0;i<11;i++) {
for(int j=0;j<11;j++) {
if(charArray[i][j]!=0) {
sum++;
}
}
}
System.out.println("sum = "+sum);
//2 .创建对应的稀疏数组
int sparseArr[][] = new int[sum+1][3] ;
//给稀疏数组赋值
sparseArr[0][0] = 11; //有11行
sparseArr[0][1] = 11; //有11列
sparseArr[0][2] = sum; //有多少个值
int count= 0; //count 用于记录是第几个非0数据
for(int i=0;i<11;i++) {
for(int j=0;j<11;j++) {
if(charArray[i][j]!=0) {
count++;
sparseArr[count][0] = i; //第0 列,第count行
sparseArr[count][1] = j; //第1列,第count行
sparseArr[count][2] =charArray[i][j];//第2列 存入的是二维数组不为0的值
}
}
}
System.out.println("输出稀疏数组的形式");
for (int[] is : sparseArr) {
for (int is2 : is) {
System.out.print("\t"+is2);
}
System.out.println();
}
}
