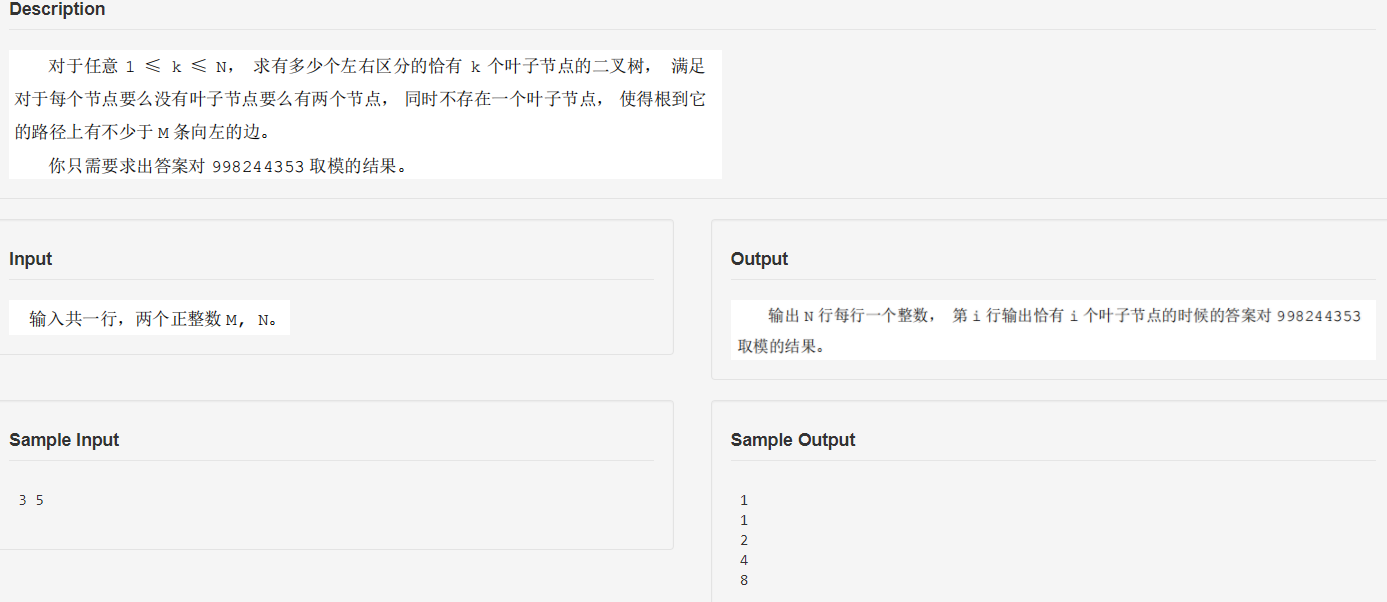
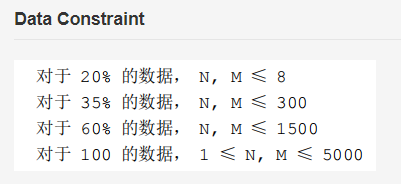
题目描述
题解
虫合
由于前几天被教♂育了,所以大力找了一发规律
先把m-1,设f[i][j]表示m≤i,有j个叶子节点的答案
转移显然,也显然是O(n^3)的
把f打出来后长这样:
1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
1 1 2 4 8 16 32 64 128 256 512 1024 2048 4096 8192
1 1 2 5 13 34 89 233 610 1597 4181 10946 28657 75025 196418
1 1 2 5 14 41 122 365 1094 3281 9842 29525 88574 265721 797162
1 1 2 5 14 42 131 417 1341 4334 14041 45542 147798 479779 1557649
1 1 2 5 14 42 132 428 1416 4744 16016 54320 184736 629280 2145600
1 1 2 5 14 42 132 429 1429 4846 16645 57686 201158 704420 2473785
1 1 2 5 14 42 132 429 1430 4861 16778 58598 206516 732825 2613834
1 1 2 5 14 42 132 429 1430 4862 16795 58766 207783 740924 2660139
1 1 2 5 14 42 132 429 1430 4862 16796 58785 207990 742626 2671892
1 1 2 5 14 42 132 429 1430 4862 16796 58786 208011 742876 2674117
1 1 2 5 14 42 132 429 1430 4862 16796 58786 208012 742899 2674414
1 1 2 5 14 42 132 429 1430 4862 16796 58786 208012 742900 2674439
1 1 2 5 14 42 132 429 1430 4862 16796 58786 208012 742900 2674440
1 1 2 5 14 42 132 429 1430 4862 16796 58786 208012 742900 2674440
显然第i行的前i+1个是正常的卡特兰数,从i+2项开始就不同了
可以发现:
\(f[1][i]=f[1][i-1]*1\)
\(f[2][i]=f[2][i-1]*2\)
\(f[3][i]=f[3][i-1]*3-f[3][i-2]*1\)
\(f[4][i]=f[4][i-1]*4-f[4][i-2]*6\)
\(f[5][i]=f[5][i-1]*5-f[5][i-2]*10+f[5][i-3]*1\)
猜想:
\(f[i][j]=\sum{f[i][j-k]*a[i][k]}\)
通过暴力枚举后可以把前几项的a搞出来:
1:1
2:2
3:3 -1
4:4 -3
5:5 -6 1
6:6 -10 4
7:7 -15 10 -1
8:8 -21 20 -5
钦定\(a[1...m][0]=1,a[1][1]=1,a[2][1]=2\)之后,可以发现一个神奇的式子:
\(a[i][j]=a[i-1][j]+a[i-2][j-1]\)
于是可以推出\(a[m]\),再推出\(f[m]\)即可
code
#include <algorithm>
#include <iostream>
#include <cstdlib>
#include <cstring>
#include <cstdio>
#define fo(a,b,c) for (a=b; a<=c; a++)
#define fd(a,b,c) for (a=b; a>=c; a--)
#define mod 998244353
using namespace std;
long long a[5001][5001];
long long f[5001];
int n,m,i,j,k,l;
int main()
{
freopen("ca.in","r",stdin);
freopen("ca.out","w",stdout);
// freopen("a.out","w",stdout);
fo(i,1,5000)
a[i][0]=1;
a[1][1]=1;
a[2][1]=2;
fo(i,3,5000)
{
fo(j,1,5000)
a[i][j]=(a[i-1][j]+a[i-2][j-1])%mod;
}
scanf("%d%d",&m,&n);
--m;
f[1]=1;
fo(i,2,m+1)
{
fo(j,1,i-1)
f[i]=(f[i]+f[j]*f[i-j]%mod)%mod;
}
fo(i,m+2,n)
{
k=1;
fd(j,i-1,1)
{
f[i]=(f[i]+f[j]*a[m][i-j]*k%mod)%mod;
k=-k;
}
}
fo(i,1,n)
printf("%lld\n",(f[i]+mod)%mod);
fclose(stdin);
fclose(stdout);
return 0;
}
官方题解
其实也不难,设\(f[i][j]\)表示放了i个点,从根到当前点需要向左走j步
那么\(f[i][j]\)可以走到自己的左儿子,或是走到最后一个向左走的那个点的右儿子,即\(f[i][j]-->f[i+1][j+1],f[i+1][j-1]\)
这样转移的本质是按dfs序走,最后的答案为\(f[2k-1][0]\)(最后一个点必定只能向右走)
code
#include <algorithm>
#include <iostream>
#include <cstdlib>
#include <cstring>
#include <cstdio>
#define fo(a,b,c) for (a=b; a<=c; a++)
#define fd(a,b,c) for (a=b; a>=c; a--)
#define mod 998244353
#define min(a,b) (a<b?a:b)
using namespace std;
int f[10001][5002];
int n,m,i,j,k,l;
int main()
{
freopen("ca.in","r",stdin);
freopen("ca.out","w",stdout);
scanf("%d%d",&m,&n);--m;
f[1][0]=1;
fo(i,1,n+n-2)
{
fd(j,min(m,i-1),0)
if (f[i][j])
{
f[i+1][j+1]=(f[i+1][j+1]+f[i][j])%mod;
if (j>0)
f[i+1][j-1]=(f[i+1][j-1]+f[i][j])%mod;
}
}
for (i=1; i<=n+n-1; i+=2)
printf("%d\n",f[i][0]);
fclose(stdin);
fclose(stdout);
return 0;
}