前言:
“十年苦琢白玉璧 一朝竞放紫兰花”
有的东西只要你肯用心学,总能学的很好。
我觉得上面这句话很适合我,毕竟就是凭着这不怕苦的精神,我才从一个连路径压缩都打不对的并查集小白成长成了普通并查集OIER(毕竟我也不是大佬 )
并查集是什么?
并查集是一种用某个代表来代表整个集合,进而再进行对集合的操作的数据结构
比如我们用3来代表{1,2,3,4,5}这个集合,我们就表示成:
p[1]=3 p[2]=3 p[3]=3 p[4]=3 p[5]=3
这里的p[a]=b就表示a属于b
长什么样?
为什么要问这个问题呢,因为这可能会对等会理解路径压缩有帮助
我们来看集合里的包含关系:
A⊊B C⊊B
A={1,2,3},C={4,5},则B={1,2,3,4,5}
我们把4拿出来当做集合B的代表,这个图就是这样子的: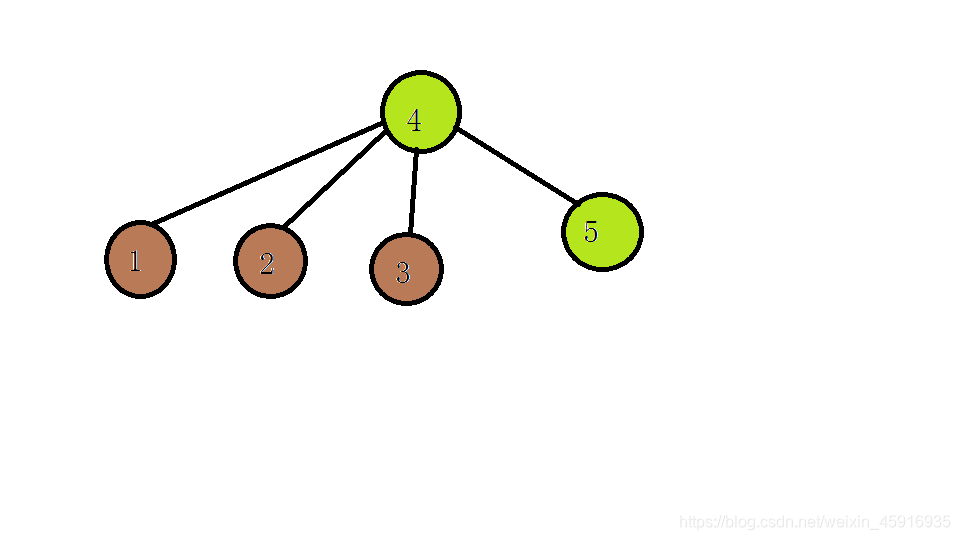
棕色代表集合A,绿色代表集合C,整个就代表B
这里集合A我没选代表…
类似的,再给出一个例子: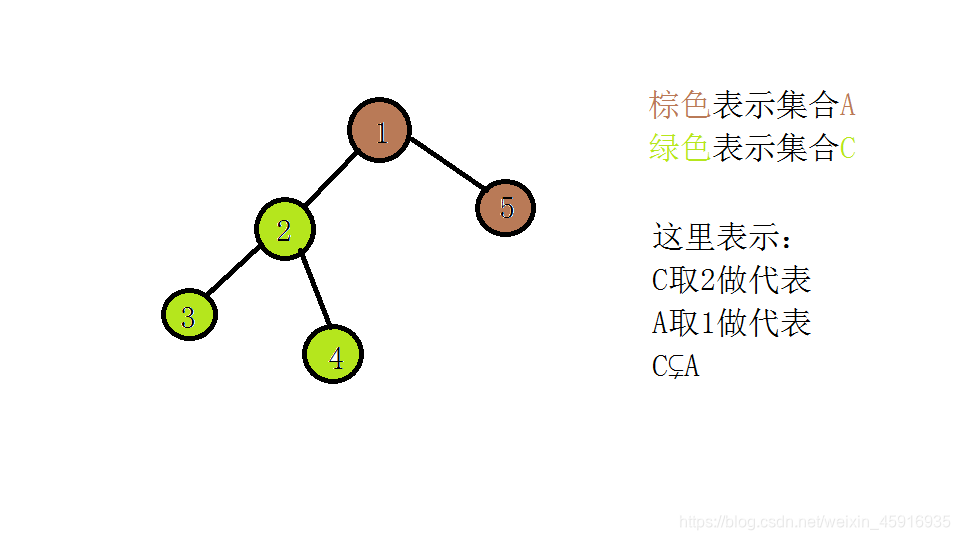
可能我的画技有点问题…
怎么写?
上文说p[x]表示的就是x所属于的集合
因此我们预处理需要这样:
void iint(){
for(int i=1;i<=n;i++) p[i]=i;//每一个元素一开始所属集合代表就是自己
}
那么我们的找集合代码就是这样写了:
int Find(int x){
if(p[x]==x) return x;
else return Find(p[x]);
}
集合间的合并就是这样:
void put(int x,int y){
p[x]=y;//x和y都是代表
}
写成普通形式就是:
void put(int a,int b){
p[Find(a)]=Find(b);//这里a和b任意取
}
但这样有点问题,我们的合并可能会退化成一条链(想想为什么?)
像这样: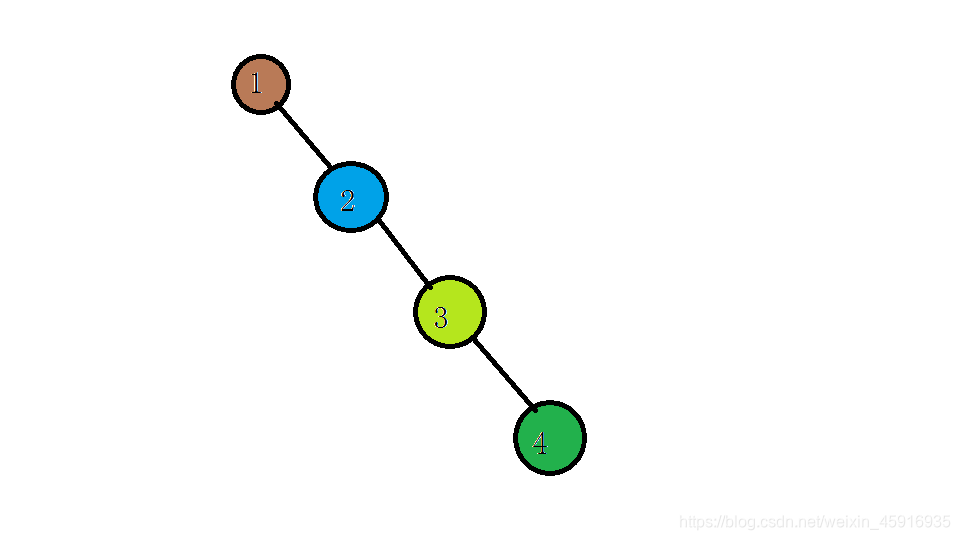
甚至可以更长
因此我们使用路径压缩来解决这个问题:
int Find(int x){
if(p[x]==x) return x;
else return p[x]=Find(p[x]);//相当于把代表一路往下改
}
除此方法还有启发性合并也能解决这个问题,但我们先把路径合并用好
标准并查集例题:
首先是模板:题目
题目描述
如题,现在有一个并查集,你需要完成合并和查询操作。输入格式
第一行包含两个整数N、M,表示共有N个元素和M个操作。接下来M行,每行包含三个整数Zi、Xi、Yi
当Zi=1时,将Xi与Yi所在的集合合并
当Zi=2时,输出Xi与Yi是否在同一集合内,是的话输出Y;否则话输出N
输出格式
如上,对于每一个Zi=2的操作,都有一行输出,每行包含一个大写字母,为Y或者N
注意,这里合并不使用路径压缩/启发性合并会超时
Code:
#include<bits/stdc++.h>
using namespace std;
inline int read(){
char c;
int res=0;
c=getchar();
while(c<'0'||c>'9') c=getchar();
while(c>='0'&&c<='9'){
res=res*10+c-'0';
c=getchar();
}
return res;
}//快读,不想用改成cin就行
int p[10001];
int Find(int k){
if(p[k]==k) return k;
else return p[k]=Find(p[k]);//路径压缩
}
int N,M,x,y,z;
int main(){
N=read();
M=read();
for(int i=1;i<=N;i++)
p[i]=i;
for(int i=1;i<=M;i++){
z=read();x=read();y=read();
if(z==1){
int X=Find(x),Y=Find(y);
p[Y]=X;//合并
}
if(z==2){
int X=Find(x),Y=Find(y);
if(X==Y)
cout<<"Y"<<endl;
else
cout<<"N"<<endl;
}
}
return 0;
}
以上就是标准的并查集
并查集拓展:
Q:为什么要拓展?
A:因为标准的并查集只能维护简单的属于与不属于信息,但我们需要它来维护更多信息。
好比你有一根3m长的钢棒和一根5m长的铁棒,
如果你用标准并查集把他们合并(焊接)在一块,那你只知道你得到了一根8m长的棒子
而组成成分(例如材料)你就一概不知
我们需要改变这个情势,因此就有了拓展
就着棒子问题,我们具体分析一下
我们焊接只考虑在最末端
我们维护一个值来代表一根棒子的长度,那么当另一根进来时,我们更新这个值(值len)
我们再维护某根棒子的头部在当前棒子里处于第几米(值sta)
那么很明显,每次合并(棒子B焊接到棒子A末尾)我们需要的操作是:
- B.sta=A.len+1;
- A.len+=B.len;
- B.len=0;//表示B已经不是独立一根棒子了
- p[B]=A
不知不觉中我们完美解决了洛谷的一道蓝题:P1196 [NOI2002]银河英雄传说
Code:
#include<iostream>
#include<cmath>
using namespace std;
const int MAXN=30001;
int p[MAXN],sta[MAXN],len[MAXN];//
int T,i,j;char c;
int Find(int x){
if(p[x]==x) return x;
else{
int k=Find(p[x]);//暂时存一下祖先
sta[x]+=sta[p[x]];//维护每根棒子长度到棒头的距离
p[x]=k;//路径压缩
return p[x];
}
}
int main(){
for(int i=1;i<=30001;i++){
len[i]=1;p[i]=i;
}
cin>>T;
while(T--){
cin>>c>>i>>j;
int x=Find(i),y=Find(j);
if(c=='M'){//合并
sta[x]+=len[y];
len[y]+=len[x];
len[x]=0;
p[x]=y;
}
else{
if(x!=y) cout<<"-1"<<endl;
else cout<<abs(sta[i]-sta[j])-1<<endl;
}
}
return 0;
}
我们把这种做法叫做边带权
我们还有一种叫扩展域的拓展,常用于当前不确定属于或不属于关系的题目
什么叫不确定属于或不属于?
这是一道模板:P1525 关押罪犯
对于每一个罪犯,我们可以维护两个值(同一间same,对面different)
当我们罪犯(A和B)间要隔离时,我们进行如下操作:
- A.different=B.same//A的对面是B
- A.same=B.different//B的对面是A
这样我们就可以维护一个隔离的关系
Code:
#include<bits/stdc++.h>
using namespace std;
const int MAXN=20001;
int p[2*MAXN];
//我们p[a]表示编号a的罪犯的同类 p[a+N]表示编号a的罪犯的对面
//这样可以不用开成两个数组
struct nod{
int u,v,val;
} node[100001];
bool cmp(nod a,nod b){
return a.val>b.val;
}
int Find(int x){
if(p[x]==x) return x;
else return p[x]=Find(p[x]);//路径压缩
}
int n,m;
int a,b,c;
int main(){
cin>>n>>m;
for(int i=1;i<=n;i++){
p[i]=i;p[i+n]=i+n;//两者隔开,因为a不可能是a的对面
}
for(int i=1;i<=m;i++)
cin>>node[i].u>>node[i].v>>node[i].val;
sort(node+1,node+m+1,cmp);
for(int i=1;i<=m;i++){
int u=node[i].u,v=node[i].v,z=node[i].val;
int x1=Find(u),x2=Find(u+n),y1=Find(v),y2=Find(v+n);
if(p[x1]==p[y1]){
cout<<z;return 0;
}else{
p[y2]=x1;
p[x2]=y1;
}
}
cout<<"0";
return 0;
}
同理还有一道题也附上代码:P2024 [NOI2001]食物链
Code:
#include<iostream>
using namespace std;
const int MAXN=50001;
int p[3*MAXN],n,m;//1本身 2捕食 3天敌
int ans;
int a,x,y;
int Find(int x){
if(p[x]==x) return x;
else return p[x]=Find(p[x]);
}
int main(){
cin>>n>>m;
for(int i=1;i<=n;i++){
p[i]=i;p[i+n]=i+n;p[i+2*n]=i+2*n;
}
for(int i=1;i<=m;i++){
cin>>a>>x>>y;
if(x>n||y>n){
ans++;continue;
}
int x1=Find(x),x2=Find(x+n),x3=Find(x+2*n);
int y1=Find(y),y2=Find(y+n),y3=Find(y+2*n);
if(a==1){
if(x1==y2||y1==x2||x3==y2){
ans++;continue;
}p[x1]=y1;p[x2]=y2;p[x3]=y3;
}if(a==2){
if(x==y){
ans++;continue;
}
if(x2==y3||x3==y1||x1==y1){
ans++;continue;
}p[y1]=x2;p[y2]=x3;p[y3]=x1;
}
}
cout<<ans;
return 0;
}
讲了那么多,我们思考一下能否用并查集维护图里面连通块间的关系
答案是肯定的,对于每条边相连的节点A和B,我们只需把A与B合并就行
那么我们反过来
能不能用并查集维护连通块内节点的删除问题?(P1197 [JSOI2008]星球大战)
答案是否定的,那我们怎么办?
其实很简单,就着这道题,我们反过来想
如果题目变成一开始给你几个点,几条边,然后每次再添加一个点(还是不重复的)和几条与之相连的边,我们怎么做
我们直接用肯定做法就能解决这个问题
是不是很简单?
如果本来两个集合通过当前添加的点变成了同一个,那么原来的连通块数就-1
如果添加的一个点是不与任一已知连通块相连(独立)的,那原来的连通块数就要+1
至此完美解决这个问题:
Code:
#include<iostream>
#include<cstring>
using namespace std;
int h[800001],to[800001],nxt[800001],tot;
inline void add(int a,int b){
to[++tot]=b;
nxt[tot]=h[a];
h[a]=tot;
}
inline void iint(int a,int b){
add(a,b);add(b,a);
}
bool vis[400010];
int n,m,K,x,y,T;
int wor[400010];
int ans[200010],pos;
int p[400010];
void dfs(int x,int root){
p[x]=root;
for(int i=h[x],v;v=to[i],i;i=nxt[i]){
if(!vis[v]&&p[v]==-1){
dfs(v,root);
}
}
}//root是当前连通块的代表
int Find(int x){
if(p[x]==x) return x;
else return p[x]=Find(p[x]);
}
int main(){
memset(p,-1,sizeof(p));//编号从0开始,所以没访问过要标记-1
cin>>n>>m;
for(int i=1;i<=m;i++){
cin>>x>>y;iint(x,y);
}cin>>K;
for(int i=1;i<=K;i++){
cin>>wor[i];vis[wor[i]]=1;
}
for(int i=0;i<n;i++){
if(p[i]==-1&&!vis[i]){
dfs(i,i);T++;//统计连通块数量
}
if(vis[i]) p[i]=i;
}
for(int i=K;i;i--){
ans[++pos]=T;
int j,v,P=-1;
vis[wor[i]]=0;
for(j=h[wor[i]];v=to[j],j;j=nxt[j]){
if(!vis[v]){
int x=Find(v);
if(P==-1) P=x;
if(P==-1) continue;
if(x!=P) T--;//通过当前节点合并成一个连通块
p[x]=P;
}
}if(P==-1) T++;//独立的一个
if(P!=-1) p[wor[i]]=P;//不是独立的
}
ans[++pos]=T;
for(int i=pos;i;i--) cout<<ans[i]<<endl;//倒序输出结果
return 0;
}
怎么说,学习是个很奇妙的过程
有的东西可能你想破头皮没想出来,结果去睡了一觉第二天就懂了
我管这一个过程叫消化
消化不能求快,应该求精
希望诸君能通过本文更好地消化并查集这一数据结构
完
来源:CSDN
作者:Mongo_w
链接:https://blog.csdn.net/weixin_45916935/article/details/103766528