前言
最近收到电力类专业同学的求助,希望能用一个算法使得从变电站至所有负载的总路线最短。当然,如果要添加特殊要求,你可以练习我的邮箱707101557@qq.com。其实应用最小生成树能够很好的解决这类问题。即给定一幅加权无向图,找到它的一颗最小生成树。此类算法主要应用是电路元器件的设计,航空航线规划,电站电力分配,图像分析等领域。
最小生成树
图的生成树是它的一棵含有其所有顶点的无环连通子图。一幅加权图的最小生成树(MST)是它的一棵权值(图中所有边的权值之和)最小的生成树。
最小生成树的经典算法
找最小生成树的两种经典算法分别是Prim算法和Kruskal算法。
Prim算法每一步都会为一棵生长中的树加一条边。一开始这看树只有一个顶点,然后会向它添加V-1条边,每次总是将下一条连接树中的顶点与不在树中的顶点且权重最小的边加入树中。
笔者只是编写了该算法Python版本,读者可以通过VisuAlgo查看该算法的动态演示过程。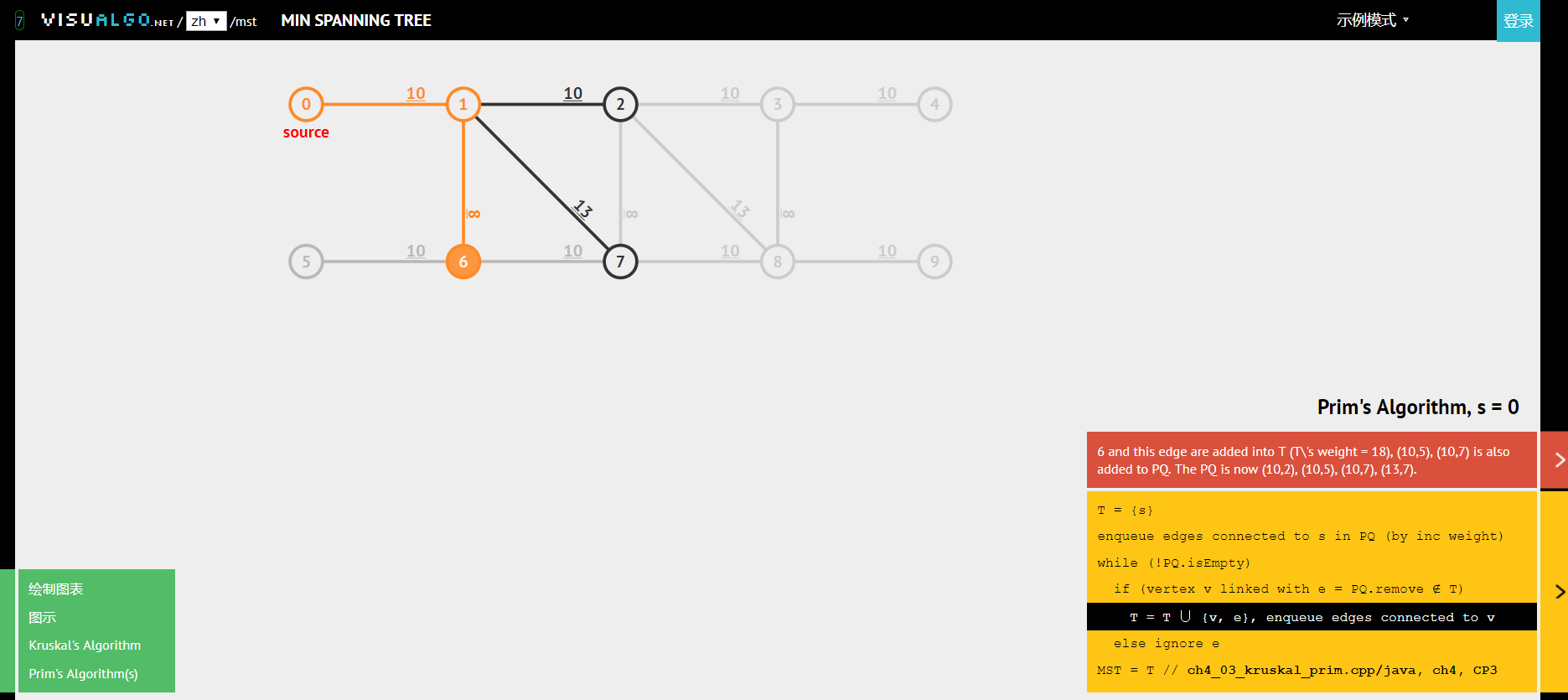
Python实现
#file @mst.py
#date @2019/10/26
#Program to find the Minimum Spanning Tree using Prim's Algorithm and Heap Data Structure
Maxint = 2**31-1
#Implementation of Heap
class Heap:
s = 0
a = []
p = {}
key = {}
def __init__(self):
self.s = -1
def heapify_up(self, i):
while i>0:
j = i//2
if self.key[self.a[i]] < self.key[self.a[j]]:
temp = self.a[i]
self.a[i] = self.a[j]
self.a[j] = temp
self.p[self.a[i]] = i
self.p[self.a[j]] = j
i = j
else:
break
def heapify_down(self,i):
j=-1
while 2*i <= self.s:
if 2*i == self.s or self.key[self.a[2*i]] <= self.key[self.a[2*i + 1]]:
j = 2*i
else:
j = 2*i + 1
if self.key[self.a[j]] < self.key[self.a[i]]:
temp = self.a[i]
self.a[i] = self.a[j]
self.a[j] = temp
self.p[self.a[i]] = i
self.p[self.a[j]] = j
i = j
else:
break
def decrease_key(self, v, key_value):
self.key[v] = key_value
self.heapify_up(self.p[v])
def extract_min(self):
ret = self.a[0]
self.a[0]=self.a[self.s]
self.p[self.a[0]] = 0
self.s-=1
if self.s>=0:
self.heapify_down(0)
return ret
def insert(self, v, key_value):
self.a.append(v)
self.s +=1
self.p[v] = self.s
self.key[v] = key_value
self.heapify_up(self.s)
def printdata(self):
print("Value of array a: ", self.a)
print("Value of p: ", self.p)
print( "Value of key: ", self.key)
#Reading data from file
if __name__ =="__main__":
f = open("input.txt")
lines = f.readlines()
f.close()
#Global variables for the Minimum Spanning Tree
Q = Heap()
n,m = map(int,lines[0].strip().split(" "))
edges = [[-1 for x in range(0,n+1)] for y in range(0,n+1)]
d = {}
pi = {}
S = []
V = []
total_weight = 0
edges_mst = [None]*(n-1)
#Add all nodes to the list V
for i in range(1,n+1):
V.append(i)
#Add all edges to the edges matrix
for i in range(0,m):
p,q,r = map(int,lines[i+1].strip().split(" "))
edges[p][q] = r
edges[q][p] = r #Adding the edges for both because it is an undirected graph
#Choosing the Arbitrary vertex as "Vertex 1"
d[1] = 0
Q.insert(1,d[1])
#Inserting the Infinity value for all other vertices
for i in range(1,n+1):
d[i] = Maxint
Q.insert(i,d[i])
#Finding the Minimum Spanning Tree
while set(S)!=set(V):
u = Q.extract_min()
S.append(u)
left = list(set(V) - set(S))
for v in left:
if edges[u][v] != -1:
if edges[u][v] < d[v]:
d[v] = edges[u][v]
Q.decrease_key(v,d[v])
pi[v] = u
#Adding the list of edges into a string array and calculating total weight
i = 0
for v in list(set(V) - set({1})):
total_weight+=edges[v][pi[v]]
if v < pi[v]:
edges_mst[i] = str(v) + " " + str(pi[v]) + " " + str(edges[v][pi[v]])
else:
edges_mst[i] = str(pi[v]) + " " + str(v) + " " + str(edges[v][pi[v]])
i+=1
#Writing Output to the file
with open("output.txt",'w') as f:
f.write(str(total_weight)+"\n")
for i in range(0, n-1):
f.write(edges_mst[i]+ "\n")
输入的测试案例input.txt
10 45
1 2 23
1 3 17
1 4 60
1 5 87
1 6 58
1 7 107
1 8 119
1 9 118
1 10 113
2 3 85
2 4 81
2 5 117
2 6 108
2 7 136
2 8 131
2 9 137
2 10 146
3 4 12
3 5 73
3 6 36
3 7 59
3 8 107
3 9 93
3 10 108
4 5 39
4 6 69
4 7 54
4 8 96
4 9 72
4 10 82
5 6 94
5 7 2
5 8 31
5 9 8
5 10 47
6 7 93
6 8 136
6 9 105
6 10 123
7 8 14
7 9 37
7 10 28
8 9 25
8 10 11
9 10 79
输出结果output.txt
162
1 2 23
1 3 17
3 4 12
4 5 39
3 6 36
5 7 2
7 8 14
5 9 8
8 10 11
系列补充
Python数据结构会是一直更新的一个系列,作者会不断补充此类算法的文章。
来源:https://blog.csdn.net/m0_37772174/article/details/102753360