原理:
激发态:原子或分子吸收一定的能量后,电子被激发到较高能级但尚未电离的状态。
每个态都有各自的势能面,都是几何坐标的函数。
振子强度小于0.01可以认为跃迁禁阻
激发态去活的途径有:①辐射跃迁(荧光或磷光 )。②无辐射跃迁(系间窜越,内部转变)。③传能和猝灭(激发态分子将能量传递给另一基态分子并使其激发)。

计算需要:
7、用高斯做激发态计算:
方法:zindo(半经验,100原子)、cis组态相互作用(50原子)、含时方法(TDDFT,gs03的时候就可以考虑溶质的影响)
Franck-condon规则:激发时核不动,垂直跃迁
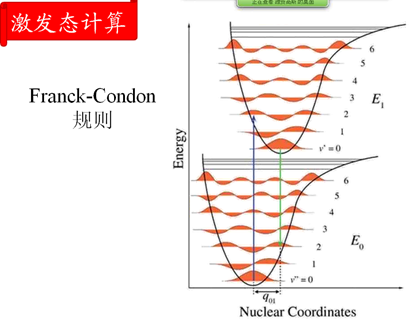


PS:知道激发能,就可以得到波长
5、溶剂在激发态计算中是必须要考虑的,溶剂效应对激发态的影响比对基态更大。特别是溶剂对光谱的影响明显不可忽略,由于溶剂与溶质的基态和激发态的相互作用不同,造成能级发生不同程度的改变,故溶剂会使吸收峰红移或蓝移。溶剂方面,TDDFT可以已经可以比较好地处理了,和主流的PCM模型可以完美地结合,可以考虑非平衡溶剂效应和做state-specific计算来响应激发态密度。需要描述与溶质间的强相互作用的时候还可以用显示溶剂模型。有时候实际外环境比较复杂,比如蛋白质环境,此时可以用QMMM或更简单的背景电荷等方式将此效应表现出来。不过,像是由于溶剂造成的谱峰展宽、光谱细节消失等等效应,不管是隐式还是显示溶剂模型都没法表现,需要做模拟,这就很复杂了。
4、在做激发态计算之前最好是先在基态下优化结构
3、可以根据激发能和振子强度绘制电子光谱图!!
2、nm, cm-1, eV之间的转换关系
波长与能量:1240/λ(nm)=x eV
波长与波数:107/λ(nm)=x cm-1
波数与能量:1240*x cm-1=eV
【其中1240的由来:(1)光量子方程E=h・ν,h为普朗克常数,ν为频率;(2)光速方程c=λ・ν,λ为波长,ν为频率。运算两个方程得到E=hc/λ,而h=4.13×10-15 eV・s,c=3×1017 nm・s,故hc=1240 eV・nm。】
1、#根据激发能和振子强度可以算激发态寿命!进而求其倒数可以得到辐射速率!!