201803-2 碰撞的小球

问题描述
　　数轴上有一条长度为L（L为偶数)的线段，左端点在原点，右端点在坐标L处。有n个不计体积的小球在线段上，开始时所有的小球都处在偶数坐标上，速度方向向右，速度大小为1单位长度每秒。
　　当小球到达线段的端点（左端点或右端点）的时候，会立即向相反的方向移动，速度大小仍然为原来大小。
　　当两个小球撞到一起的时候，两个小球会分别向与自己原来移动的方向相反的方向，以原来的速度大小继续移动。
　　现在，告诉你线段的长度L，小球数量n，以及n个小球的初始位置，请你计算t秒之后，各个小球的位置。
提示
　　因为所有小球的初始位置都为偶数，而且线段的长度为偶数，可以证明，不会有三个小球同时相撞，小球到达线段端点以及小球之间的碰撞时刻均为整数。
　　同时也可以证明两个小球发生碰撞的位置一定是整数（但不一定是偶数）。
输入格式
　　输入的第一行包含三个整数n, L, t，用空格分隔，分别表示小球的个数、线段长度和你需要计算t秒之后小球的位置。
　　第二行包含n个整数a1, a2, …, an，用空格分隔，表示初始时刻n个小球的位置。
输出格式
　　输出一行包含n个整数，用空格分隔，第i个整数代表初始时刻位于ai的小球，在t秒之后的位置。
样例输入
3 10 5
4 6 8
样例输出
7 9 9
样例说明
　　

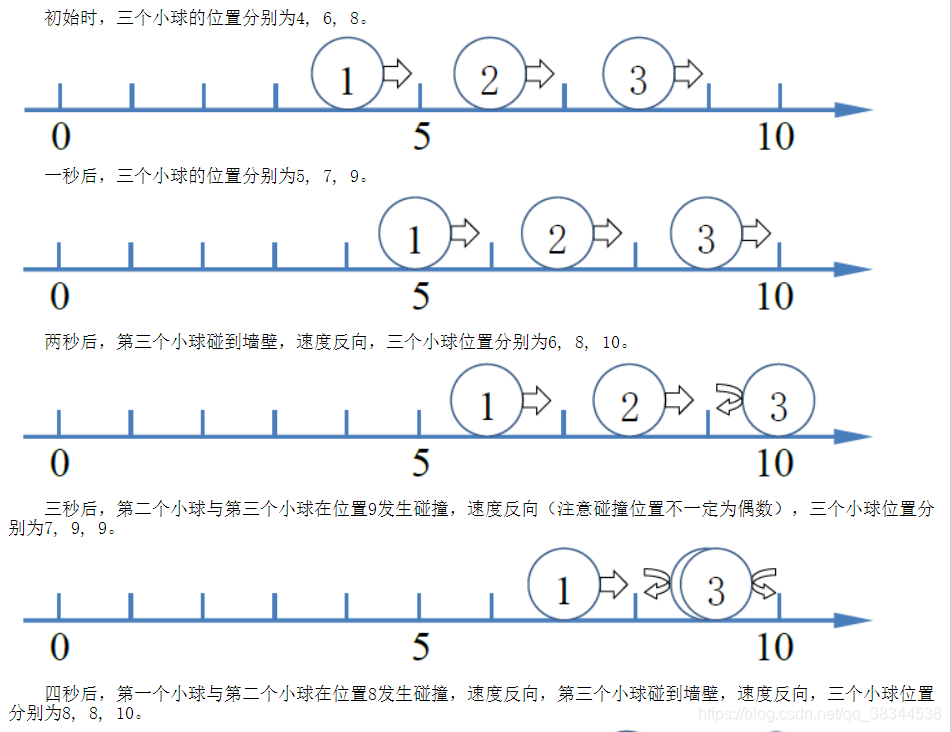
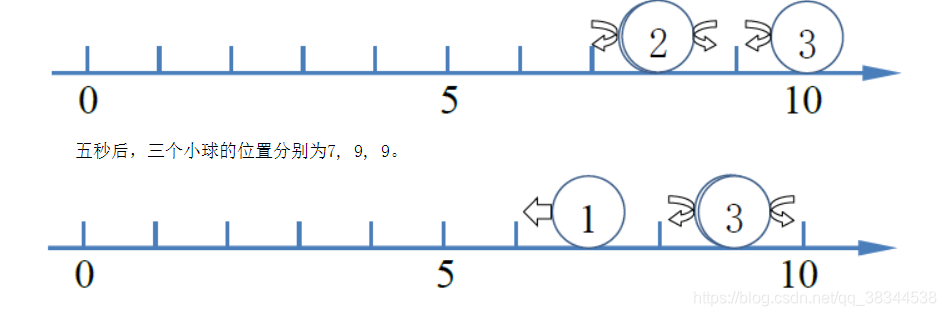
样例输入
10 22 30
14 12 16 6 10 2 8 20 18 4
样例输出
6 6 8 2 4 0 4 12 10 2
数据规模和约定
　　对于所有评测用例，1 ≤ n ≤ 100，1 ≤ t ≤ 100，2 ≤ L ≤ 1000，0 < ai < L。L为偶数。
　　保证所有小球的初始位置互不相同且均为偶数。

暴力模拟实现

#include <iostream>

using namespace std;


int main()
{
    int x,y,m,n,i,j,k,l,t,f;
    int num[101],flag[101];
    cin>>n>>l>>t;
    for(i=1;i<=n;i++)
    {
        cin>>num[i];
        flag[i]=1;
    }
    for(j=1;j<=t;j++)
    {
        for(k=1;k<=n;k++)
        {
            f=0;
            // 在两端调转方向
            if(num[k]==0||num[k]==l)
            {
                flag[k]=-flag[k];
                num[k]=num[k]+flag[k];
                continue;
            }
            // 查看有没有重合碰撞
             for(i=k+1;i<=n;i++)
             {
                 if(num[k]==num[i])
                 {
                     flag[k]=-flag[k];
                     flag[i]=-flag[i];
                     num[k]=num[k]+flag[k];
                     f=1;
                     break;
                 }
             }
             //如果没发生碰撞和没到边界
            if(f==0)
            {
                num[k]=num[k]+flag[k];
            }
        }
    }

     for(i=1;i<=n;i++)
    {
        cout<<num[i]<<' ';

    }
    return 0;
}

来源：CSDN

作者：zhimin魏魏魏

链接：https://blog.csdn.net/qq_38344538/article/details/104089792