现有的很多量化方法都是通过量化后重训练来弥补量化损失的，但这些方法并不完美：它们需要完整的数据集（这涉及到隐私及其他问题），而且还需要大量的计算资源。于是，一种被称为post-training的方法被踢出了：它不需要完整的数据集，也不需要重新训练或微调模型（也就是说，可以达到端对端），且它的准确率与流行的浮点模型的精度接近。
但这类方法一旦把量化精度放到8bit以下时，精度就大幅下降。为了解决这个问题，本文提出了一种利用网络分布的统计信息来最小化在量化过程中引入的本地误差。
ACIQ: Analytical Clipping for Integer Quantization
作者提出了三种方法，第一种是应用于激活层，其形式为：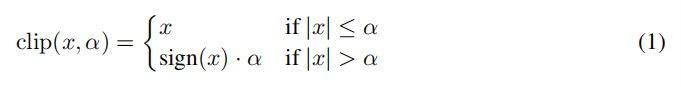
由于[-α，α]被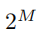
均分，因此设间隔Δ：
作者又假设量化前的值位于每个小区间的中心处（由大数定理知，这个假设是可行的），于是量化的方差为：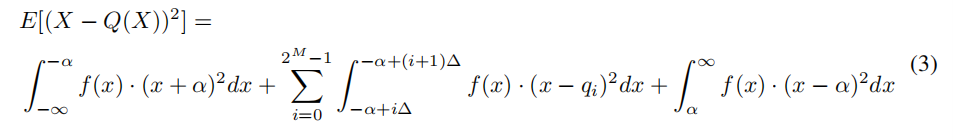
这里X是量化前的值，Q(X)是量化后的值，作者假设X满足一个均值为零的分布（如高斯分布或拉普拉斯分布。因为能够加上或减去均值，所以这种假设并不使方法失去一般性）。上式的前后两项，由于分布是对称的，所以是相等的，作者称之为裁剪噪音；中间项则称为量化噪音。
随后作者用了两个式子来近似这两个误差：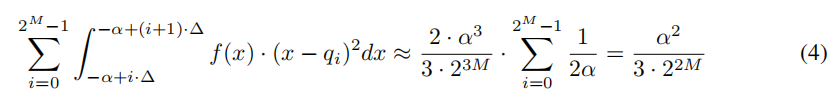
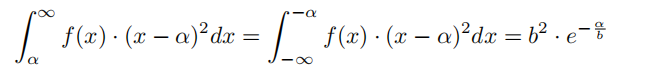
于是式3最终变为
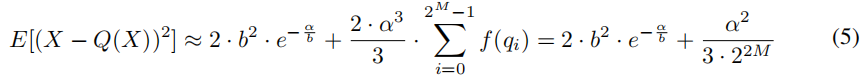
这里的b大概是来自作者假设的权重分布Laplace(0, b)。
引入这个方程后，我们就可以通过最小化MSE的方式来学习α了：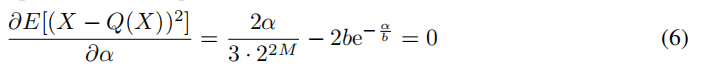
对M=2，3，4，α∗ = 2.83b, 3.89b, 5.03b。在实践中，ACIQ方法的b的估计方法为b = E(|X - E(X)|)
Per-channel bit-allocation
这个方法同时应用在权重和激活层上。它的中心思想是，在不改变整体的权重和激活层的位数的前提下，给每个通道不同的位数来提升量化精度。
设共有n个通道，且B为总共的位数。设i层使用[-α,α]将值量化为Mibit，于是根据式5有以下函数：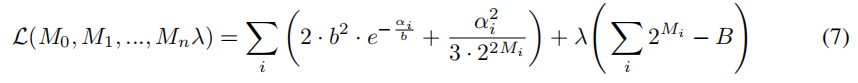
对Mi求导有：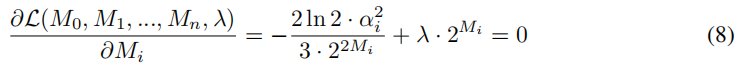
对λ求导有：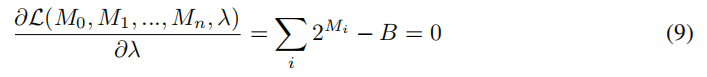
结合8、9有
两边取2的对数：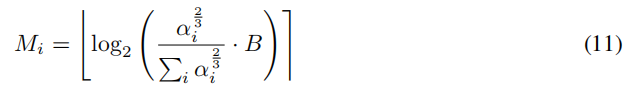
这里取整是因为Mi是整数。
Bias-Correction
该方法应用于权重。
作者观察到，在量化值中存在固有的权重的均值和方差值的偏置，设权重Wc为通道c的权重，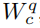
是它的量化后的版本。则有：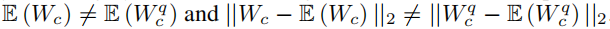
为了弥补这个偏置，作者计算了以下统计值：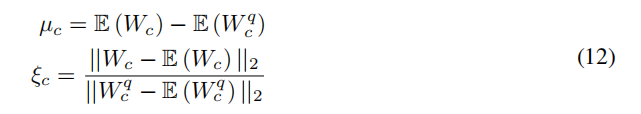
并将其应用于后续计算（这是在线下做的）：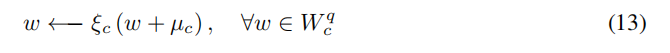
随后作者说他曾考虑将ACIQ和偏置方法都同时应用于权重和激活层。但因为权重裁剪没有用，而激活层统计信息无法在线下获得，进而无法在post-training方法中实现。
来源：CSDN
作者：JachinMa
链接：https://blog.csdn.net/JachinMa/article/details/104040527