adding values to diagonals of matrix using element-wise addition in matlab

问题

I am writing a script that operates on matrices, and I have run into the problem of needing to add the sum of the diagonals of a previous matrix to the diagonal elements of a new matrix. The code I have so far for this particular function (described in more detail below) is:

t = 1;
for k = (m-1):-1:-(m-1)
    C = bsxfun(@plus, diag(B, k), d);
    g(t) = sum(diag(B, k));
    t = t + 1;
end

where d is a 1x3 array, and C is supposed to be a 3x3 array; however, C is being output as a 1x3 array in such a way that the first diagonal is being summed and added to d, then the main diagonal is being summed and added to d, and the final diagonal is being summed and added to d.

Is there a way I can get the values of C to be such that the first diagonal is the sum of it's individual elements added to the last element of d, the main diagonal's individual elements added to the middle element of d, and the bottom diagonal's elements added to the first element of d? (while still working for any array size?)

Here is a picture that describes what I'm trying to achieve:

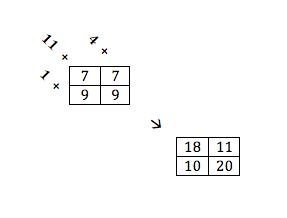
Thanks!

回答1:

You can use toeplitz to generate a matrix containing the values that need to be added to your original matrix:

M = [5 5 5; 7 7 7; 9 9 9]; %// data matrix
v = [1 11 4 3 2]; %// data vector
S = toeplitz(v);
S = S(1:(numel(v)+1)/2, (numel(v)+1)/2:end);
result = M+S;

Or, as noted by @thewaywewalk, you can do this more directly as follows:

M = [5 5 5; 7 7 7; 9 9 9]; %// data matrix
v = [1 11 4 3 2]; %// data vector
result = M + toeplitz(v(size(M,1):-1:1), v(size(M,2):end));

回答2:

Assuming B to be a square shaped matrix, listed in this post would be one bsxfun based vectorized approach. Here's the implementation -

N = size(B,1) %// Store size of B for later usage

%// Find a 2D grid of all indices with kth column representing kth diagonal of B
idx = bsxfun(@plus,[N-numel(B)+1:N+1:N]',[0:2*N-2]*N)  %//'

%// Mask of all valid indices as we would see many from the 2D grid 
%// going out of bounds of 2D array, B
mask = idx>numel(B) | idx<1

%// Set all out-of-bounds indices to one, so that in next step 
%// we could index into B in a vectorized manner and sum those up with d
idx(mask)=1
sum1 = bsxfun(@plus,B(idx),d(:).') %//'

%// Store the summations at proper places in B with masking again
B(idx(~mask)) = sum1(~mask)

Sample run -

B =
     1     9     0
     7     9     4
     6     8     7
d =
     4     9     5     8     2
B =
     6    17     2
    16    14    12
    10    17    12

回答3:

Code:

The following code adds the sums of the diagonals of A to the corresponding diagonals in the matrix B. The code works for matrices A, B of equal size, not necessarily square.

A = magic(4);
B = magic(4); 

D = bsxfun(@minus, size(A,2)+(1:size(A,1)).', 1:size(A,2)); %'
sumsDiagsA = accumarray(D(:), A(:)); %// Compute sums of diagonals (your 'd')
B = B + sumsDiagsA(D); %// Add them to the matrix

Explanation:

First we build a matrix that numbers all diagonals beginning from the rightmost diagonal:

>> D = bsxfun(@minus, size(A,2)+(1:size(A,1)).', 1:size(A,2))
D =
     4     3     2     1
     5     4     3     2
     6     5     4     3
     7     6     5     4

Then we compute sumsDiagsA as the sum of the diagonals via accumarray:

sumsDiagsA = accumarray(D(:), A(:));

The variable sumsDiagsA is what you refer to as d in your code.

Now we use indexing to the vector containing the sums and add them to the matrix B:

C = B + sumsDiagsA(D);

Assuming you have already computed your vector d, you don't need the accumarray-step and all you need to do is:

D = bsxfun(@minus, size(B,2)+(1:size(B,1)).', 1:size(B,2)); %'
C = B + d(D);

来源：https://stackoverflow.com/questions/29000277/adding-values-to-diagonals-of-matrix-using-element-wise-addition-in-matlab

标签

arrays

matlab

matrix