make efficient the copy of symmetric matrix in c#

问题

I want to store in an array a symmetric matrix

for a matrix I was doing this

    double[,] mat = new double[size,size];
    for (int i = 0; i < size; i++)
    {
      for (int j = 0; j <= i; j++)
           mat[i, j] = mat[j, i] = (n * other_matrix[i,j]);
    }

If I want to store in an array

double[] mat = new double[size*size];

instead of

 double[,] mat

What would be the most efficient way?

using mat[i*n+j]?

回答1:

Yes.

Store the elements by row, where the i-th row and j-th column is stored in index k=i*NC+j with NC the number of columns. This applies to a non-symmetric general matrix.

To store a symmetric matrix of size N you only need N*(N+1)/2 elements in the array. You can assume that i<=j such that the array indexes go like this:

k(i,j) = i*N-i*(i+1)/2+j            i<=j  //above the diagonal
k(i,j) = j*N-j*(j+1)/2+i            i>j   //below the diagonal

with

i = 0 .. N-1
j = 0 .. N-1

Example when N=5, the array indexes go like this

| 0   1   2   3   4 |
|                   |
| 1   5   6   7   8 |
|                   |
| 2   6   9  10  11 |
|                   |
| 3   7  10  12  13 |
|                   |
| 4   8  11  13  14 |

The total elements needed are 5*(5+1)/2 = 15 and thus the indexes go from 0..14.

The i-th diagonal has index k(i,i) = i*(N+1)-i*(i+1)/2. So the 3rd row (i=2) has diagonal index k(2,2) = 2*(5+1)-2*(2+1)/2 = 9.

The last element of the i-th row has index = k(i,N) = N*(i+1)-i*(i+1)/2-1. So the last element of the 3rd row is k(2,4) = 5*(2+1)-2*(2+1)/2-1 = 11.

The last part that you might need is how to go from the array index k to the row i and column j. Again assuming that i<=j (above the diagonal) the answer is

i(k) = (int)Math.Floor(N+0.5-Math.Sqrt(N*(N+1)-2*k+0.25))
j(k) = k + i*(i+1)/2-N*i

To check the above I run this for N=5, k=0..14 and got the following results:

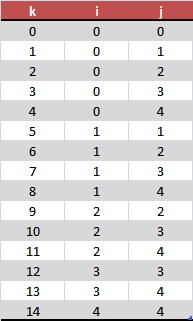
Which is correct!

To make the copy then just use Array.Copy() on the elements which is super fast. Also to do operations such as addition and scaling you just need to work on the reduced elements in the array, and not on the full N*N matrix. Matrix multiplication is a little tricky, but doable. Maybe you can ask another question for this if you want.

回答2:

Regarding the selected answer, unless I am being a complete idiot the code isn't correct:

Try this:

i = 2, j = 1

therefore we use:

k(i,j) = j*N-j*(j-1)/2+i

to find the index k, solving:

k(i,j) = 1*5 - 1*(1-1)/2 + 2

k(i,j) = 5 - 0 + 2 = 7

From the matrix in the selected answer we see that (2,1) is not 7, it seems to be 6. In fact (since this seems to be 0-base), 7 occurs at (3,1) or (1,3). The second formula for i > j seems to be inaccurate unless I am missing something.

UPDATE:

This seems to work if you alter the i > j formula to:

k(i,j) = j*(N-1)-j*(j-1)/2+i

回答3:

If n is the size of the square matrix, you need n * (n + 1) / 2 total values for a symmetric matrix. This is the sum of 1 + 2 + 3 + ... (n - 2) + (n - 1) + n.

A word of caution, though, it's going to be a big pain to be always trying to calculate the correct index for a given row and column, and I'd only move away from the more intuitive 2D array if the matrices are going to be large, and memory is going to be an issue.

来源：https://stackoverflow.com/questions/9039189/make-efficient-the-copy-of-symmetric-matrix-in-c-sharp

标签

loops

matrix