条件概率
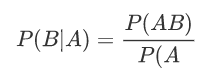
乘法公式
全概率公式
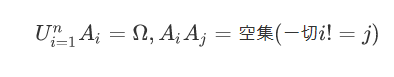
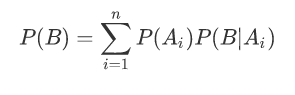
根据小偷们的资料,计算村子今晚失窃概率的问题:P(Ai)表示小偷 i 作案的概率,P(B|Ai)表示小偷i 作案成功的概率,那么P(B)就是村子失窃的概率
贝叶斯公式(又称逆概公式)
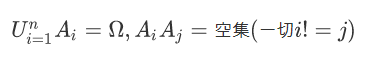
P(Ai)>0,则对任一事件B,只要P(B)>0,有
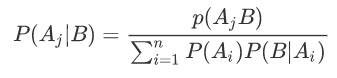
若村子今晚失窃,计算哪个小偷嫌疑最大的问题(嫌疑最大就是后验概率最大)
假设小偷1和小偷2在某村庄的作案数量比为3:2,前者偷窃成功的概率为0.02,后者为0.01,现村庄失窃,求这次失窃是小偷1作案的概率。
【分析】A1={小偷1作案},A2={小偷2作案},B={村庄失窃}

总结:
先验概率P(A):在不考虑任何情况下,A事件发生的概率条件概率P(B|A):A事件发生的情况下,B事件发生的概率后验概率P(A|B):在B事件发生之后,对A事件发生的概率的重新评估全概率:如果A和A'构成样本空间的一个划分,那么事件B的概率为:A和A'的概率分别乘以B对这两个事件的概率之和。
朴素贝叶斯的直观理解
案例:
有一个训练集包含100个人,其中有60个非洲人(黑卷47,黑直1,黄卷11,黄直1),有40个亚洲人(黑卷1,黄卷4,黄直*35),请训练朴素贝叶斯模型。
肤色x1={黑,黄}, 发型x2={卷,直}; 地区label={亚,非}
先计算先验概率:
亚洲人的比例m,非洲人的比例
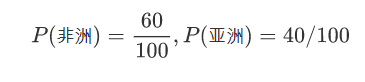
模型构建:根据资料计算模型参数
亚洲人中肤色=黑的比例,亚洲人中肤色=黄的比例
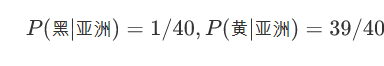
非洲人中肤色=黑的比例,非洲人中肤色=黄的比例
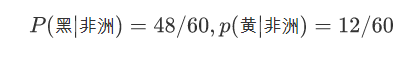
亚洲人中发型=卷的比例,亚洲人中发型=直的比例
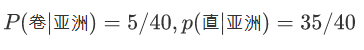
非洲人中发型=卷的比例,非洲人中发型=直的比例
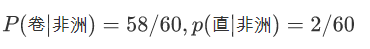
假设新来了一个人【[黑,卷],地区=?】,请用朴素贝叶斯模型预测这个人的地区。Y表示地区,X表示特征向量,根据贝叶斯公式,并假设特征间独立的假设有:

和特征间独立的假设(朴素),得

根据计算结果,模型会将这个人的地区预测为非洲。
朴素:假设特征间是独立的(忽略肤色和发型的联系),从而变成了“低配版的贝叶斯模型”,称为“朴素贝叶斯”。
优点:是可以减少需要估计的参数的个数;缺点:会牺牲一定的分类准确率。
如果是贝叶斯模型的话,模型参数总数为:
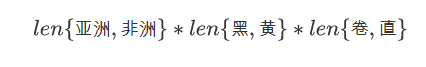
是指数增长的,实际是不可行的;而朴素贝叶斯模型参数总数为:
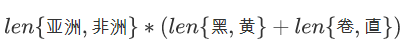
通过朴素贝叶斯就可以避免线性增长。
训练:先根据数据集,计算标记(地区)的先验概率,再计算每一个特征(肤色和发型)的条件概率,这些概率值就是模型参数,因此朴素贝叶斯的训练成本很低。
预测:当一个【黑,卷】来报道时,假设特征间是独立的,朴素贝叶斯模型会预测他的老家是非洲的,原理就是
“非洲人的概率 非洲人里肤色为黑的比例 非洲人里发型为卷的比例 > 亚洲人的概率 亚洲人里肤色为黑的比例 亚洲人里发型为卷的比例”。
朴素贝叶斯模型会将实例预测为后验概率最大的类。
继续上文的引例,考虑一个这样的问题:
假设某人的地区完全依靠其肤色的就能确定,发型是一个对判断地区没有参考价值的特征,假设P(卷|非洲)=0, P(卷|亚洲)=0.001,当来了一个【黑,卷】人的时候,我们算出

然后被预测为亚洲人,傻了吧?
原因:出现某个模型参数为0时,0乘任何数都=0,直接影响到后验概率的计算结果。
解决这一问题的方法是使用平滑操作,改造先验概率公式:

改造每个特征的条件概率公式(这里只列举了2个):

在随机变量各个取值的频数上赋予一个正数,当λ=1时,称为拉普拉斯平滑

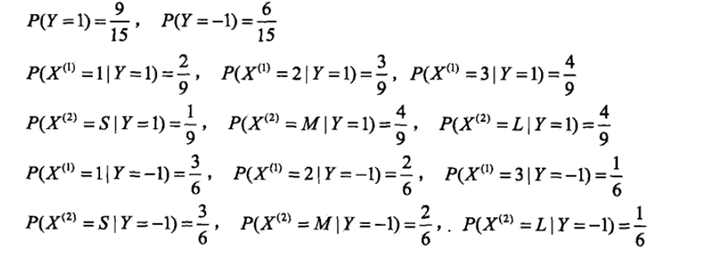



拉普拉斯平滑
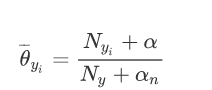
17: 15+2 (拉普拉斯平滑)
10: 9+1 (拉普拉斯平滑)
代码实现
多项式朴素贝叶斯:
当特征是离散变量时,使用多项式模型
高斯朴素贝叶斯:
当特征是连续变量时,使用高斯模型
伯努利朴素贝叶斯:
伯努利模型和多项式模型是一致的,但要求特征是二值化的(1,0)
注意:当特征中既有连续变量又有离散变量时,一般将连续变量离散化后使用多项式模型