关键词：离群点检测、生成潜在离群点、维数诅咒、生成性对抗主动学习、模式崩溃问题、多目标生成性对抗主动学习

1.INTRODUCTION

1.1 Outlier Detection应用领域

异常轨迹
运动目标检测
欺诈检测
新兴主题检测
医疗信息检测

1.2存在的问题

需要足够多的正常、异常的标签（非常昂贵）

通过假设整个数据集只包含正常实例，异常检测通常被认为是一类分类问题。最直接的方法是为所有样本创建一个模型，然后根据与建立的正常配置文件的偏差计算离群值。
具体方法有基于统计的模型、基于回归的模型、基于集群的模型、基于重构的模型，它们对正常数据的生成机制做出了不同的假设。

问题： 缺乏关于数据特征的先验信息，很难选择合适的模型和参数。

1.3AGPO-baesd方法

通过生成潜在的异常值来创建标记数据集。然后，任何现成的分类器都可以用于后续的检测。
最直观的方法是从均匀分布中抽取潜在的异常值。然而，由于数据在高维空间中的稀疏性，有限数量的潜在异常值可能无法提供足够的信息来帮助分类器描述一个清晰的边界，从而将异常值与正常数据分离开来。

为了解决这个问题，已经做了一些工作来生成发生在真实数据内部或附近的数据点。例如，一类分类方法综合了基于真实数据密度估计的潜在异常值;然而，它需要对数据的基本分布做出假设。
基于主动学习的方法通过不确定抽样从随机生成的数据中选择信息样本;然而，由于日益复杂的数据结构，并不能保证始终保持良好的性能.

2.用于异常检测的生成式对抗主动学习

2.1 SO-GAAL

为了解决“curse of dimensionality”造成的信息缺失问题，将生成式对抗学习框架应用于离群点检测，该方法在SO-GAAL中实际执行了一个主动的学习过程。

2.1.1 背景

G:生成器（生成与真实数据相似的样本）
D:判别器（有效估计数据来自真实数据P或者生成器G的概率）
判别模型和生成模型是深度学习领域的两大模型。然而判别模型已经研究的较好（由于反向传播、dropout、relu激活函数的出现），生成模型却由于概率计算困难（最大似然估计计算难）加上不好使用relu函数，使其发展较为缓慢。

2.1.2 GAN模型

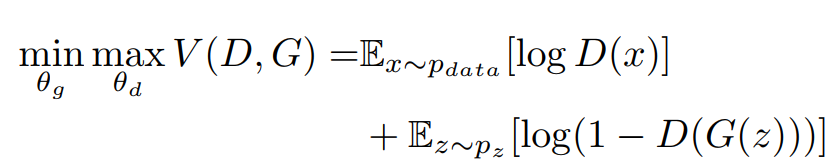
SO-GAAL

2.1.3 运行结果

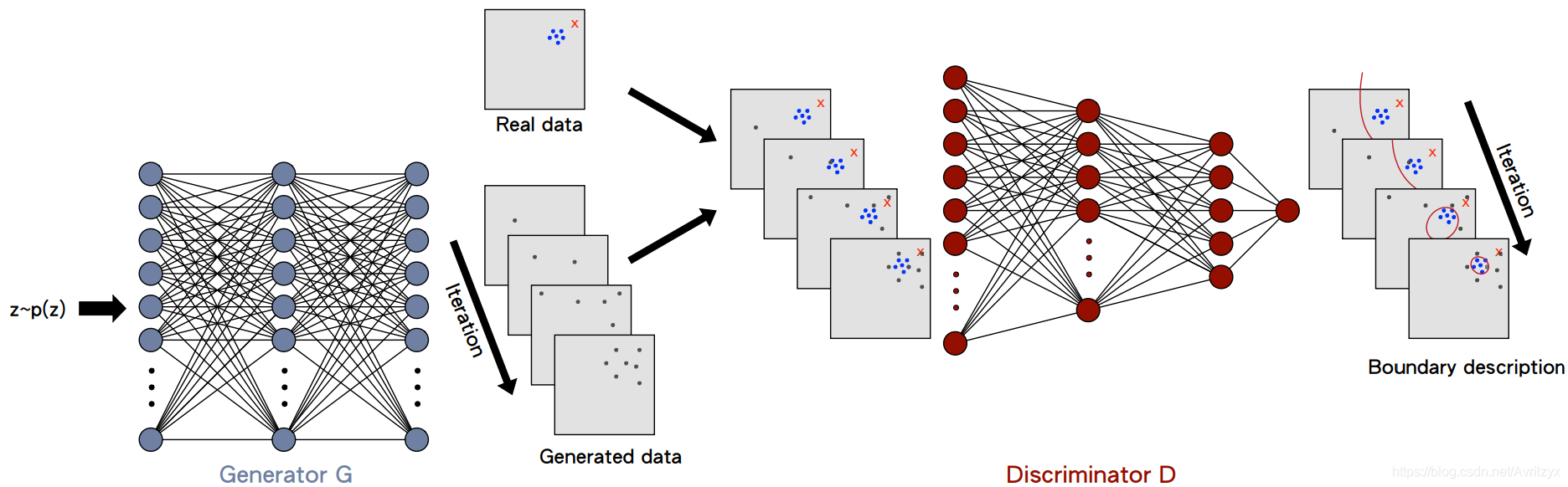
SO-GAAL
在训练的早期阶段，G可能无法生成足够数量的潜在异常值(如图中的灰点所示)。这使得D通过一个粗略的边界(用红线表示)将生成的数据与真实数据分开。
但是，经过几次迭代之后，G逐渐了解了生成机制，并合成了越来越多的潜在异常值，这些异常值出现在真实数据内部或接近真实数据的地方. 结果表明，G能够准确地描述包含集中法线数据点的分割边界。
G通过生成信息潜在异常值有效地提高了D的准确性，这实际上是一个主动的学习过程。

2.1.4 优点及问题

与现有的基于主动学习的异常检测方法相比，SO-GAAL可以直接生成有价值的数据点。此外，由于生成对抗学习框架的强大学习能力，G可以捕获复杂数据结构的深层表示，而无需对生成机制进行任何假设，这更有可能提供一致的良好结果。

第一个问题是G应该采用什么样的网络结构?
如果G采用sigmoid和默认初始权值的随机网络结构，则生成的数据可能会聚集到样本空间的中心(即，所有输出值均在0.5左右);然后移动到实际数据所在的区域，形成集群，这与SO-GAAL的上述优化过程不一致。
为了解决这个问题，使用了全连接的网络结构、ReLU、一个随机的正交初始权值

第二个问题是需要多少次迭代才能保证鉴别器D准确描述边界?
由于低维，在前100次迭代中，当生成的潜在异常值仍然分散在样本空间中时，所有的异常值都可以被识别(AUC=1)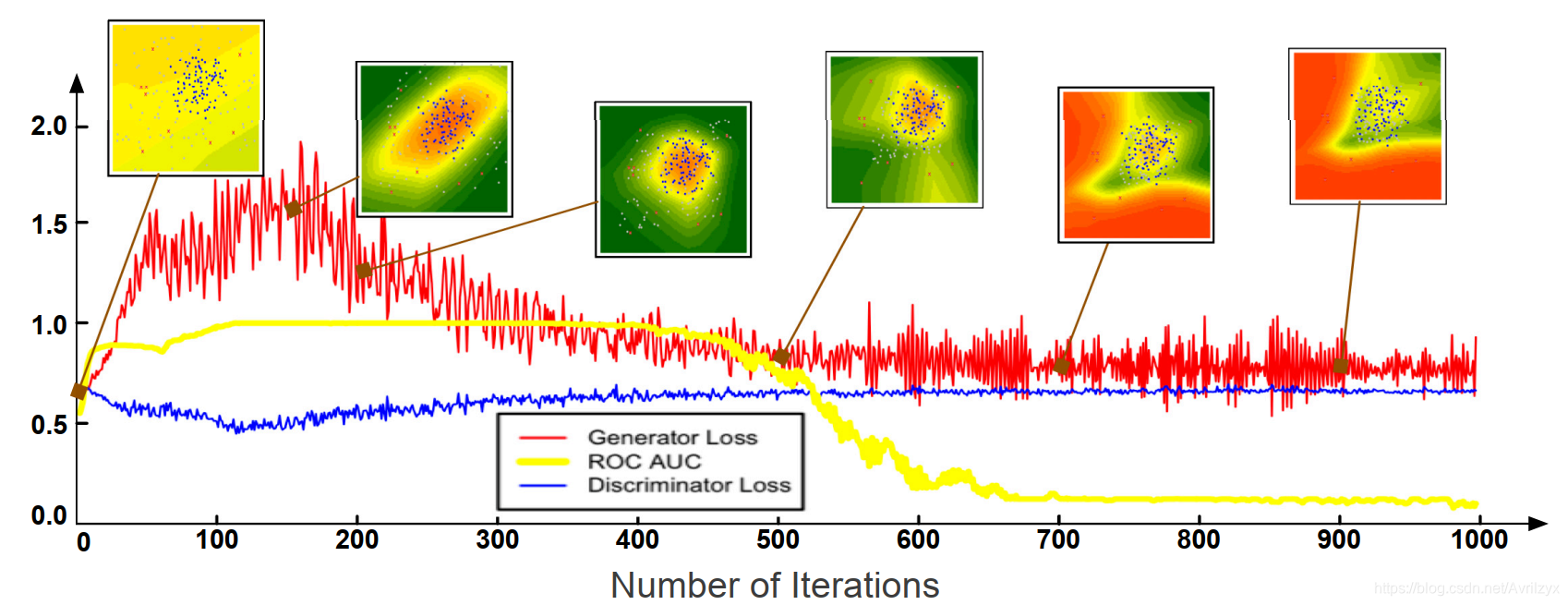
lterations
然而,随着mini-max博弈达到纳什均衡,精度急剧下降。
模式崩溃：*随着训练的进行，所有的信息潜在异常值都出现在真实数据的内部或附近，导致一些正常示例面临比异常值更高的密度参考分布。
因此，为了防止这个问题，当潜在的异常值能够提供足够的信息时，应该确定训练的停止节点。

对于SO-GAAL来说，这是非常困难的，因为在培训阶段没有预先的信息。为了提供一个高级的解决方案，我们将结构从单个生成器扩展到多个具有不同目标的生成器(MO-GAAL)，从而为整个数据集生成多个参考分布的混合
单个生成器生成的异常值可能聚集在某个正常值附近，导致其他地方就没办法判断，用多个生成器的话，可以将相似的x分到一块给每个子生成器，每个子生成器有一个分布，这样就会比一个单独的分布准确

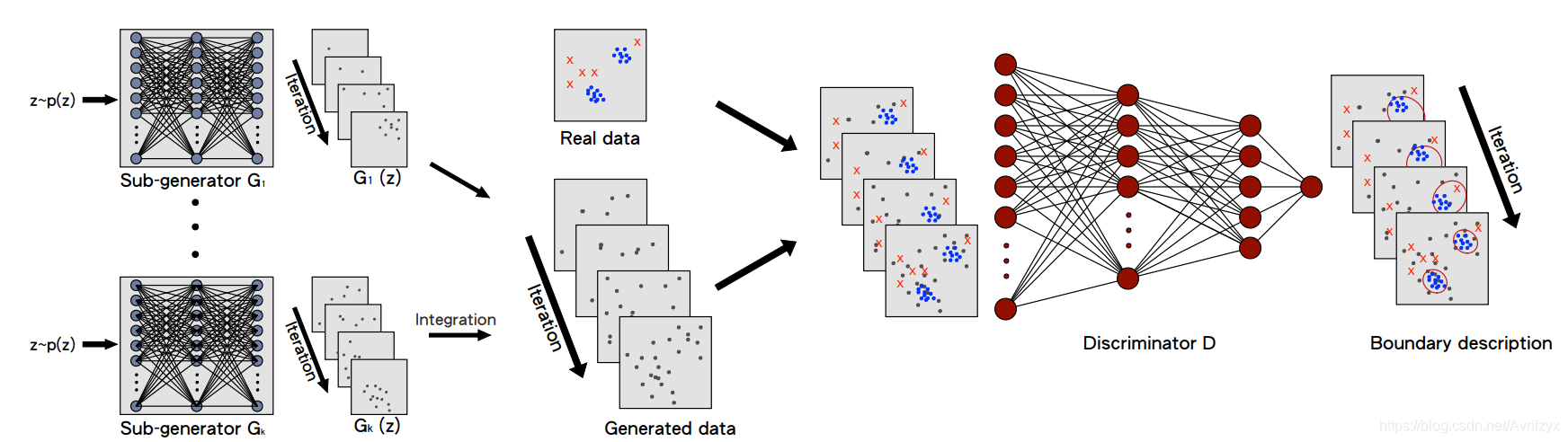
2.2 MO-GAAL

2.2.1 模型

K个sub-G
1个D
原理： Gi学习真实数据集Xi中的数据X，对不同Gi生成的异常值进行积分得到参考分布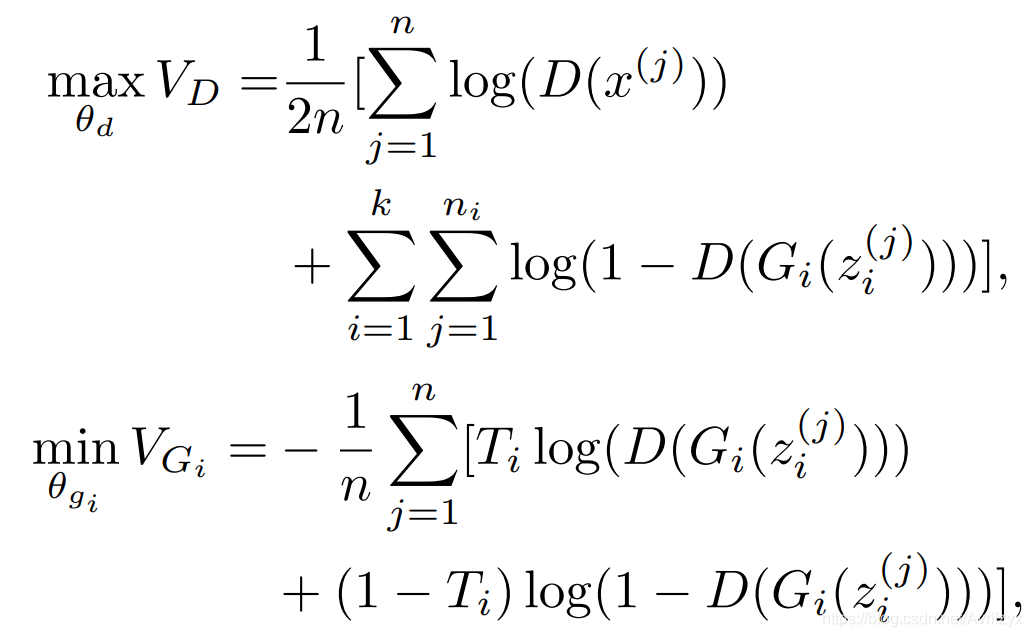
SO-GAAL

根据其相似输出D(x)，将数据集分成K份
相似输出是指空间平滑过渡的逆过程（输出相似的样本在样本空间中更有可能彼此相似，每个子集的数据也有可能彼此相似）
生成与Xi相似的值
sub-G的目标值D（Gi（Z））从1变成Ti

2.2.2 运行结果

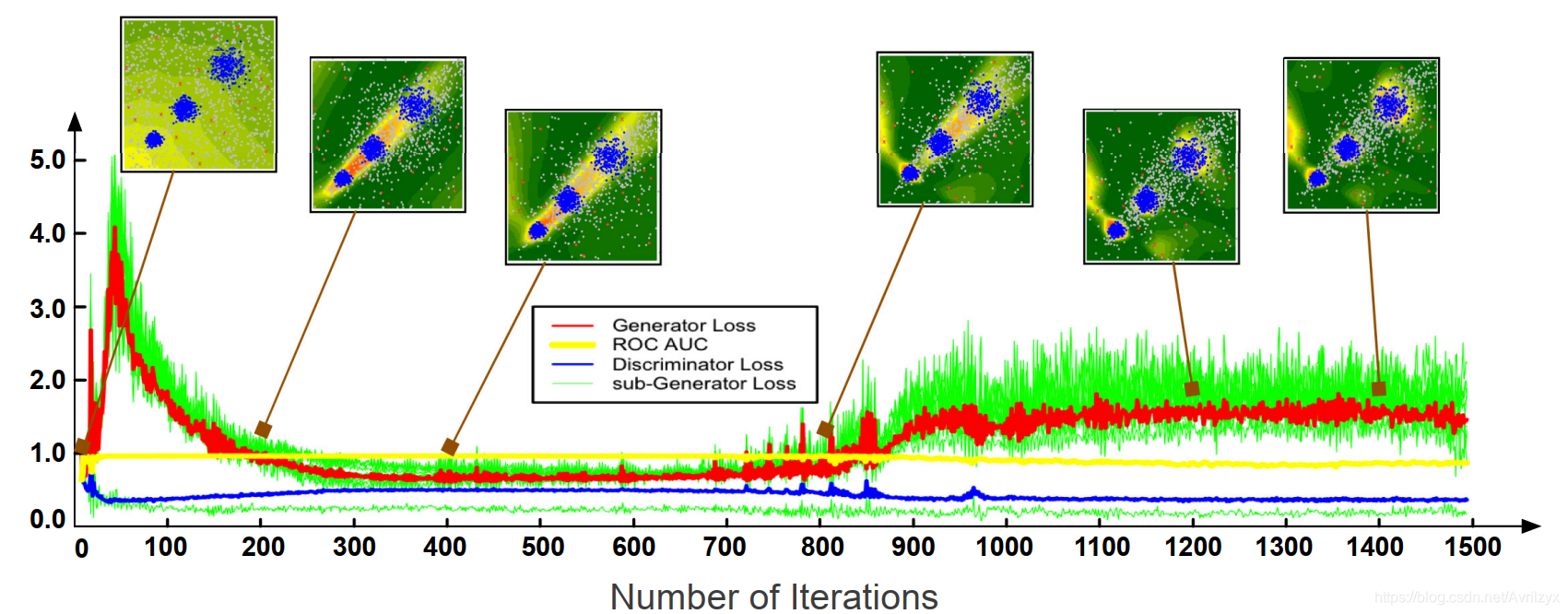
lterations
MO-GAAL的性能和优化过程在前期迭代中与SO-GAAL基本相同。但是，当mini-max博弈达到Nash均衡(在300到400次迭代期间)时，MO-GAAL的离群点检测精度在多集群数据集上仍然保持较高的水平。 证明了集成的子生成器Gi对整个实际数据有合理的参考分布。最后，当纳什均衡达到时，我们停止训练子生成器Gi，然后继续训练鉴别器D，直到它的参数几乎没有更新。

3.实验设置

3.1 数据集

1.真实数据集

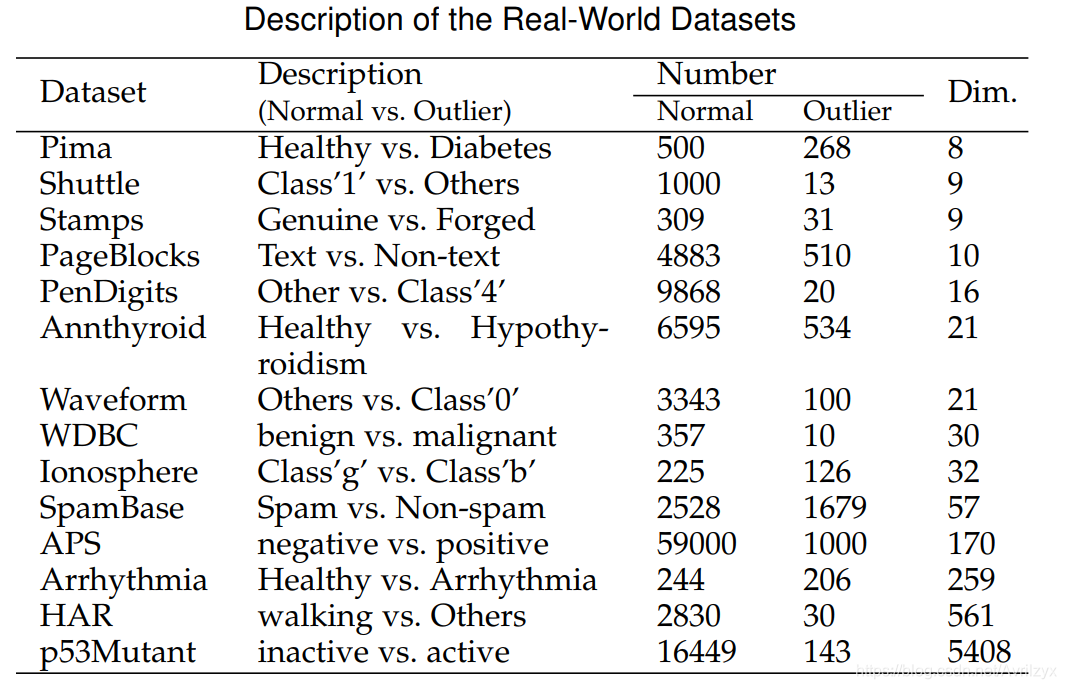
real-datasets
其中前10个为常出现在异常检测中的基准数据集，后四个为高维数据集

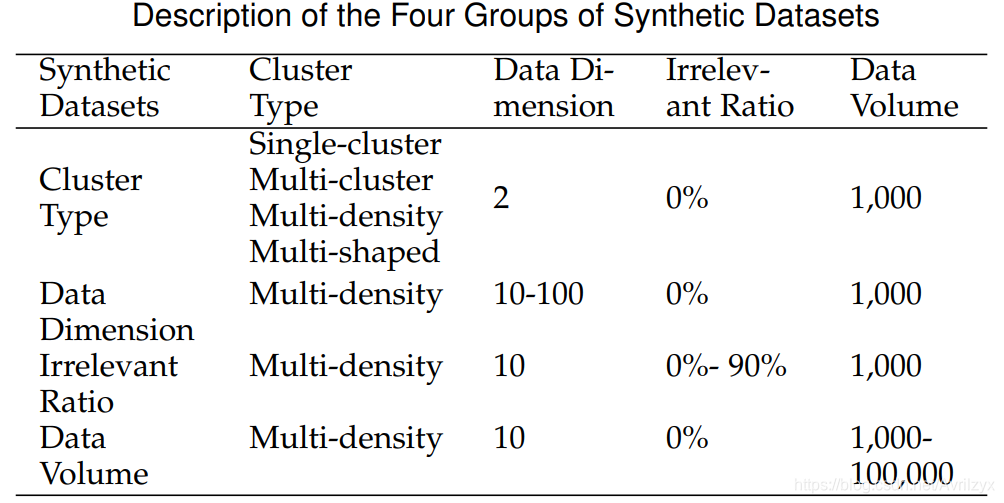
2. 合成数据集

考虑了四个方面生成数据：

聚合类型：single-cluster, multi-cluster, multidensity and multi-shaped
数据维度
变量不相干比率
数据量（评估复杂度）

synthetic datasets

3.2 评价方法

使用ROC曲线和相应的AUC来测量检测精度，而不受异常值个数的影响。此外，为了比较多个数据集上的多个模型，执行了一个非参数统计检验(即弗里德曼)。
弗里德曼的零假设是，所有算法之间没有显著差异。如果统计量超过了规定的显著性水平的临界值，则拒绝原假设，并进行事后检验(即Nemenyi)

3.3 常见异常检测方法

3.3.1 基于模型的方法（最直接的方法）

它为所有样本创建一个模型，然后预测那些与建立的profiles有较大偏差的异常值。这个方法需要选择合适的模型和参数。
例如:高斯混合模型(GMM)将整个数据集拟合为混合高斯分布，并通过期望最大化或深度估计网络对参数进行评估。然而，GMM需要预先确定适当的集群类型和数量，这是非常重要和非常困难的。

3.3.2 基于重构的方法

如PCA、矩阵分解(MF)和深度自编码，**通过压缩和解压缩将实例映射到输出，并将重构误差较大的点识别为离群点 **。
与PCA和MF的主要区别在于，自动编码器在建模复杂的数据分布时的能力更强。

3.3.3 一分类支持向量机（OC-SVM）

对数据分布没有任何假设。它的目标是找到一个超平面，可以在投影的高维空间中把绝大多数数据从原点分离出来。

3.3.4 基于邻近度的方法

它不需要对数据集进行任何训练或假设。它们是通过测量点的稀缺性来执行的，例如到第k个最近邻的距离或局部可达性密度(LOF)的比值。

4.实验结果

4.1 在合成数据集的实验

4.1.1 Results on cluster type datasets

auc
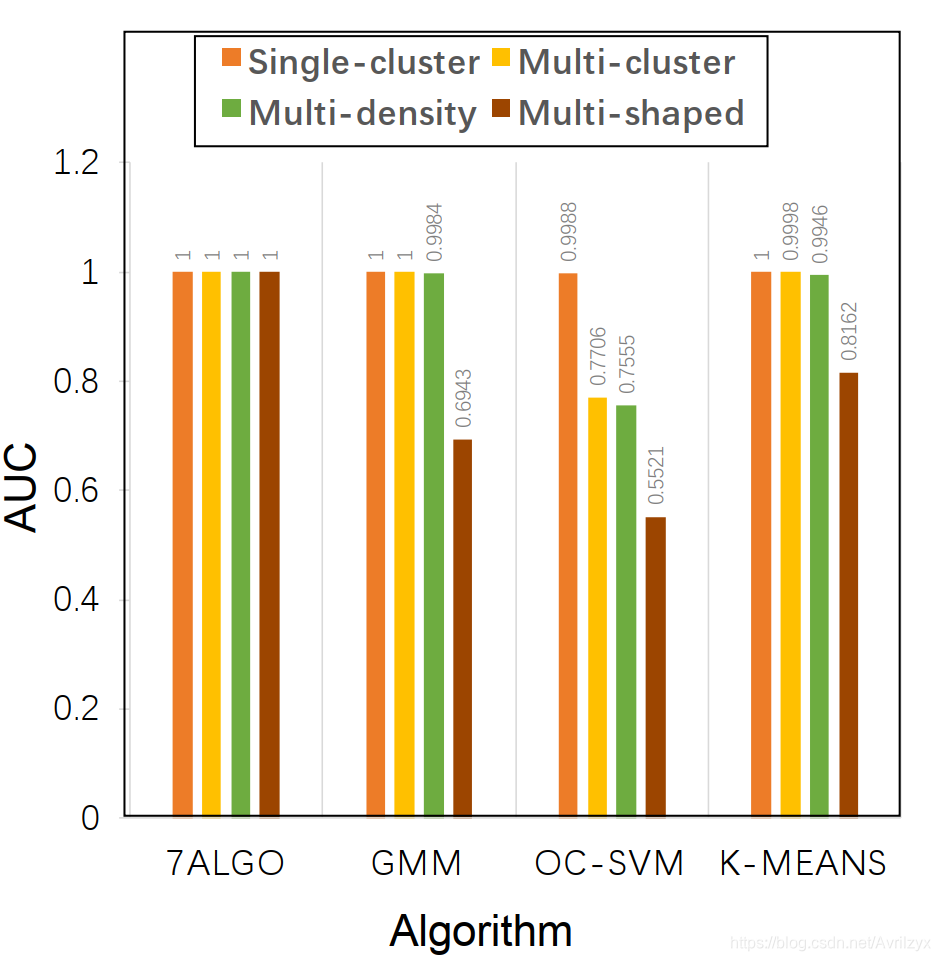
几乎所有的算法都可以在单聚合数据集上获得良好的结果(AUC近似等于1)，
但是随着聚合的复杂度的v增加，GMM、k-means和OC-SVM的性能下降:由于GMM和kmeans的假设不能满足多形数据集，它们描述了错误的划分边界。虽然oc - svm可以表征复杂的边界，但在复杂的聚类类型下，由于只有一个全局的核宽度，oc - svm更容易受到异常值的影响。
而MO-GAAL等算法或显式或隐式地遵循离群值的假设是非集中的，在处理上述问题时具有显著的优势

4.1.2 Results on data dimension datasets and irrelevant ratio datasets

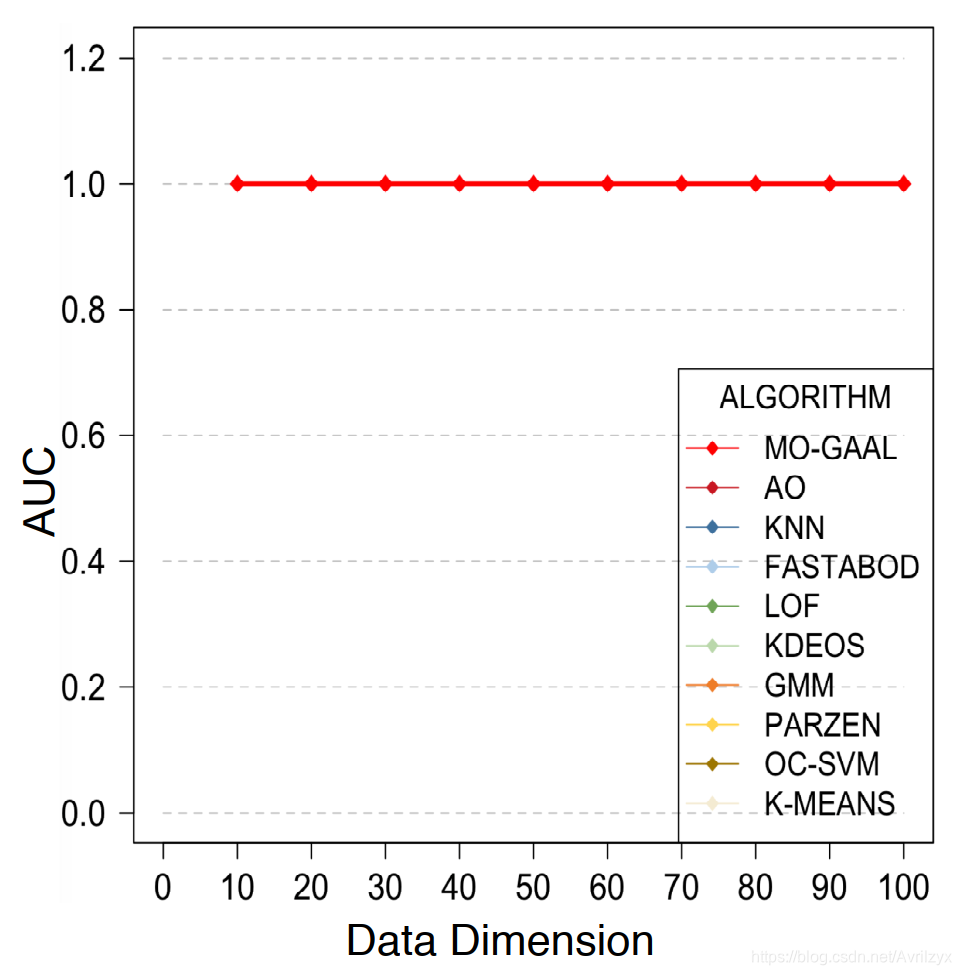
当各变量相关时，各模型均能得到令人满意的结果(AUC = 1)，虽然近、远邻之间的距离测量存在轻微的集中效应，但是所有的方法都可以更容易、更稳定地获得异常值的准确排序。这是因为增加的相关变量在异常值和正常数据之间有显著的不同行为，这些行为通过提供更多有区别的信息来帮助异常值识别。
但在固定维数的情况下，各算法的性能均随着无关变量比例的增大而降低. 涉及到距离计算的方法，如k-means、kNN、FastABOD、LOF、KDEOS等，减少得更快。这是因为在相邻的查询结果中，相关的属性被大量不相关的变量所掩盖。
不相关变量是异常检测“维数诅咒”问题的核心。而基于agpo的异常检测算法(如MO-GAAL和AO)用于评价浓度没有距离计算和形状限制的样本，在对抗无关变量引起的噪声方面有明显的优势.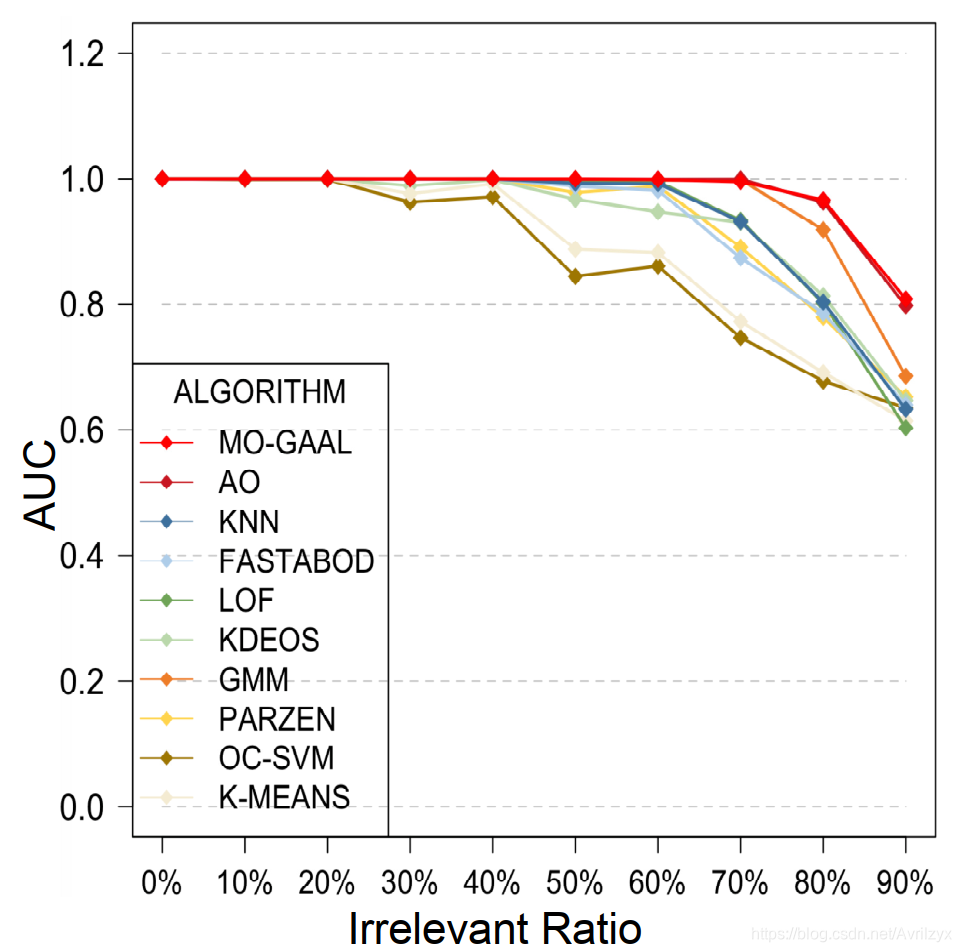

4.1.3 Results on data volume datasets

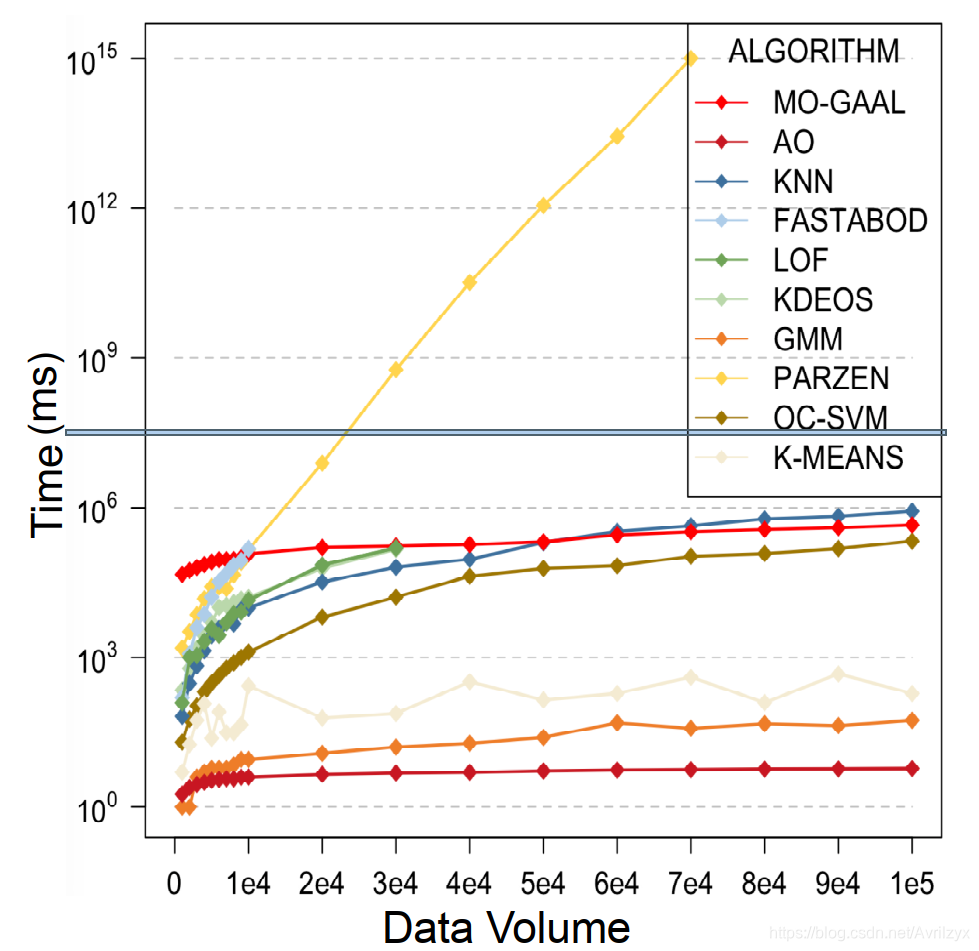
对小数据集没有优势，但随着计算能力的提高，在大数据集上，MO-GAAL的计算需求随着n的增加而线性增加，这是完全可以接受的。

4.2 在真实数据集的实验

real
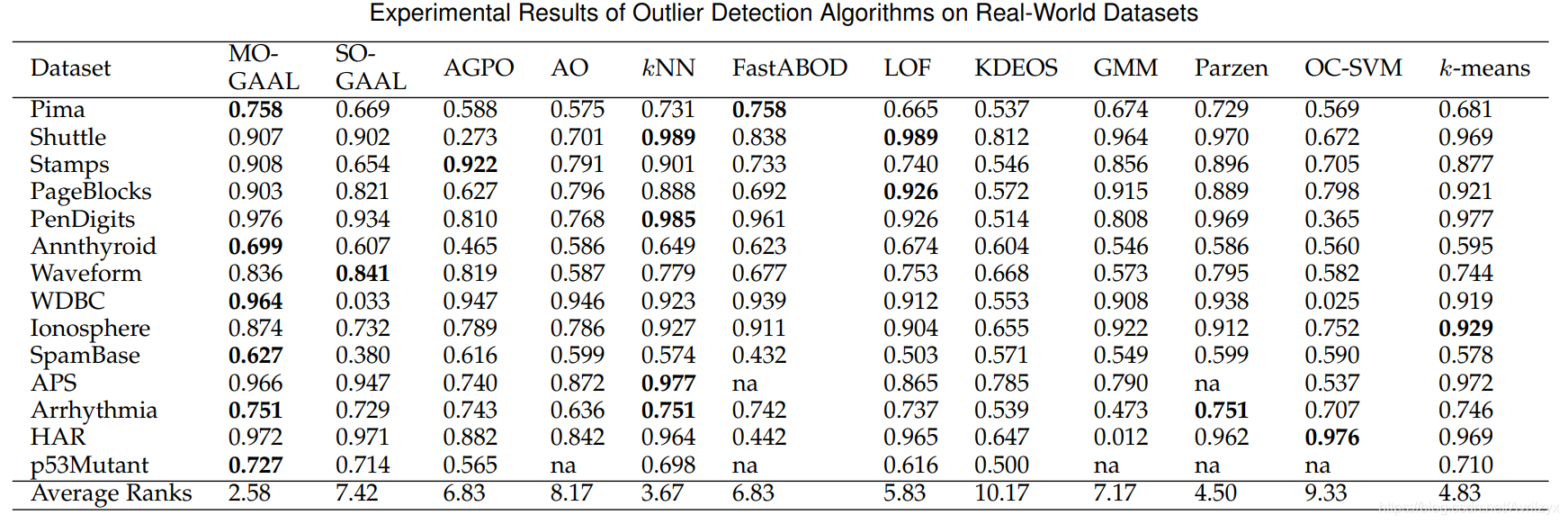
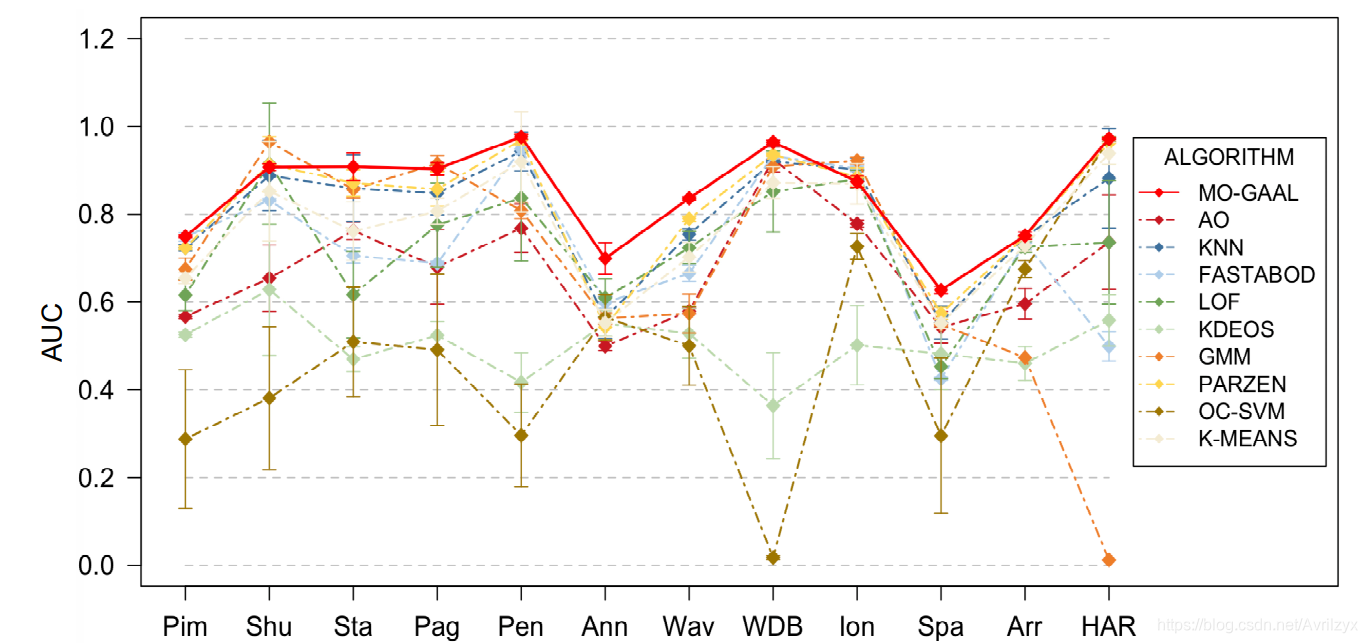
MO-GAAL在14个数据集中的6个数据集上获得了最高的精度。特别是随着维数的增加，MOGAAL更容易获得较好的结果。但是仅仅比较最优结果的数量是不够的。为了在多个数据集上综合比较这些方法，应用了Friedman检验。
弗里德曼检验的零假设是假设所有比较算法之间没有显著差异。 即在N个数据集上k个算法的平均秩Rj应该是相似的，其中rji是第i个数据集上第j个算法的秩。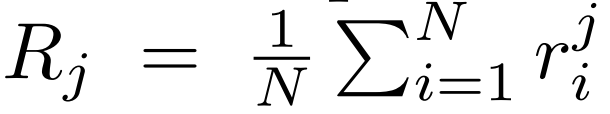

如果一个算法由于数据集的大小而没有产生结果，那么该数据集(例如，APS和p53Mutant)在计算平均秩时将不被考虑。
弗里德曼统计量的计算方法如下：（遵循自由度为k-1的分布）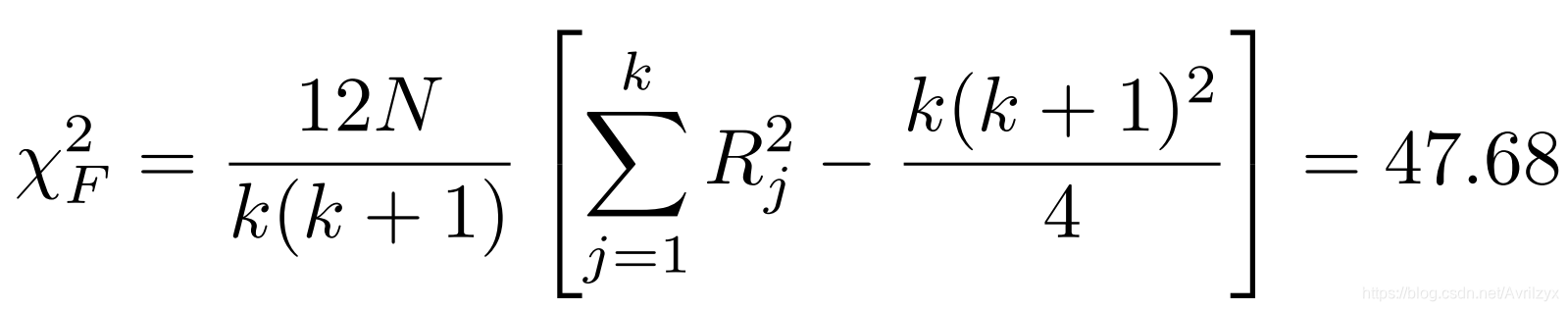

在置信度为95%的情况下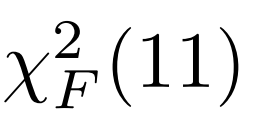，在这里插入图片描述的临界值为19.68，可以得出其零假设被拒绝。
然后进行Nemenyi测试，评估两种算法的性能是否存在显著差异。Nemenyi的临界差分(CD)如下: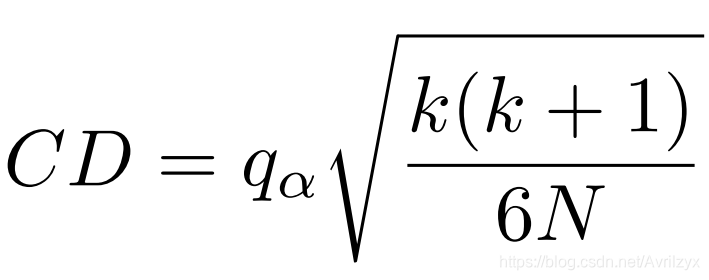

q在α= 0:1和α= 0:05的临界值分别为3.030和3.268，与之对应的临界差分CD为4.460和4.810。
关于检验的理论解释

然后，比较了两种算法的平均秩，并在表中显示了一些显著的Nemenyi检验结果。注意，符号“+”和“++”表示90%和95%的置信度下，列算法优于行算法，有90%和95%的置信度，符号“−”和“−−”是相反的。
在这里插入图片描述

MO-GAAL在95%置信水平下优于AO，KDEOS和OC-SVM，在90%的置信水平上优于GMM。
从这个地方来看，直接生成潜在异常值的MO-GAAL比通过不确定抽样的方式选择信息势异常值的AO具有明显的优势
抽样。
MO-GAAL与其他五种离群点检测算法无显著差异
(即 kNN, LOF, FastABOD, Parzen和k-means)
然而，根据参数的不同，其他的结果可能会有很大的差异，并且最好的结果不一定总是保证的。然而，在大多数情况下，MO-GAAL可以获得良好的结果。
MO-GAAL在95%置信水平上优于SO-GAAL。虽然SO-GAAL在波形上优于MO-GAAL，但它在其他一些数据集上表现不佳。这取决于生成器在陷入模式崩溃问题之前是否停止训练。这说明了不同目标的多个生成器的必要性，可以提供更友好、稳定的结果。

4.3 网络结构的鲁棒性实验

1.子生成器k的数量

子生成器k的数量是SO-GAAL到MO-GAAL性能提升的关键，因此调整这样的超参数是主要关注点之一。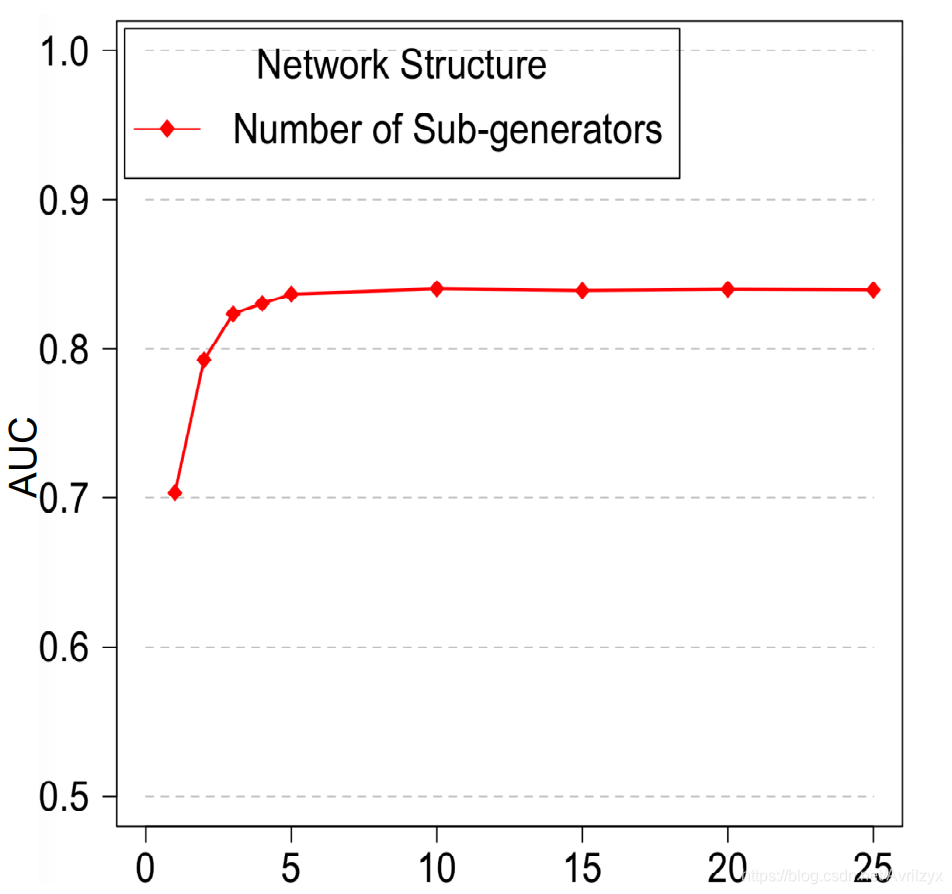
k变化
我们将k的取值范围设定为1 ~ 25，不同k的MO-GAAL在真实数据集上的结果如上图)所示。当模型中只有一个发生器时，也就是SO-GAAL，由于模模型崩溃问题，模型的平均结果明显低于其他有多个子发生器的模型。
然后，随着k的增加，模型的性能从0:7增加到0:84，当k达到一定的大小时保持稳定。也就是说，MO-GAAL对k不敏感。

2.神经网络的学习能力

学习能力
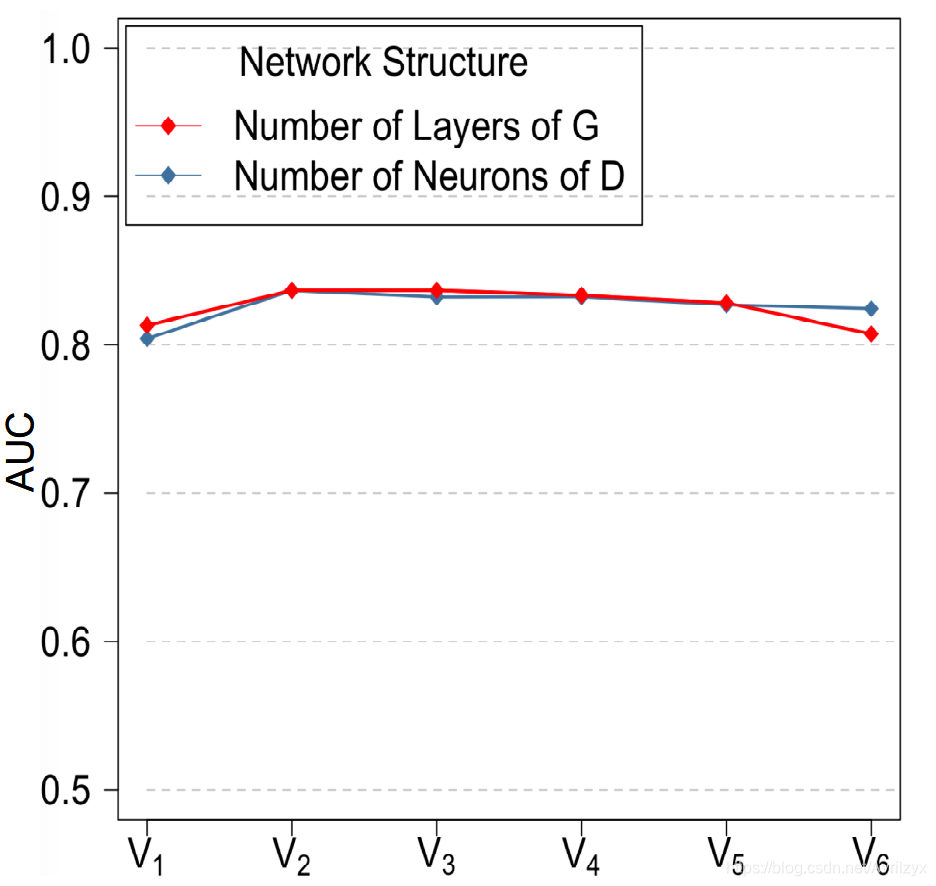
调整了生成器的层数(从2到7)和鉴别器的隐含层神经元的层数(从
分别是二分之根号3倍根号n)。
可以看出，2层生成器(如图红线所示)的检测能力略差，因为不足的生成器不能产生足够的信息潜在异常值。
而过多的隐含层(如7层生成器)，由于鉴别器相对较弱，也可能对模型性能产生轻微影响。
对于鉴别器(如图蓝线所示)，当其隐含层神经元数量较少时，由于欠拟合，其性能略低于其他神经元数量充足的模型。也就是说，只要发生器和鉴别器的网络结构变化在合理范围内，MO-GAAL就是鲁棒的。

5.总结与展望

提出了一种新的异常检测算法SO-GAAL，该算法能够直接生成潜在的信息异常值。
此外，将GAAL的结构从单个生成器(SO-GAAL)扩展到多个具有不同目标的生成器(MO-GAAL)，以防止生成器陷入模式崩溃问题。
与几种先进的异常检测方法相比，MO-GAAL算法在真实数据集上获得了最好的平均排名，并对参数的变化具有很强的鲁棒性。
此外，MO-GAAL可以很容易地处理各种簇类型和高度不相关的变量比，这可以从合成数据集上的实验结果得到证明。
尽管它的运行时对小数据集没有优势，但随着计算能力的提高，它并不是一个致命的缺陷
此外，MO-GAAL的计算需求随着数据量的增加而线性增加，这是完全可以接受的。
未来，可以尝试将集成学习引入到GAAL的迭代优化或特征选择中，以获得更令人满意和稳定的结果，并将对不同数据类型的网络结构进行更深入的研究。

来源：CSDN

作者：H轩轩轩轩哥哥

链接：https://blog.csdn.net/Avrilzyx/article/details/103157496

标签

异常值

Generative Adversarial Active Learning for Unsupervised Outlier Detection