莱布尼兹命题9 《几何原本》公理2和亚里士多德的“相同”
-逻辑与算法之十三
在莱布尼兹的片断20中,从命题9开始,对命题的证明都辅之以几何图形。无论如何抽象的几何图形,也比纯粹文字的表述更容易为人理解。在759中曾给出过片断20命题3的文字证明,本篇再给出片断20中,逻辑加交换律命题1的文字证明。然后,则仅给出有辅助图形的命题9及其证明。
这个思路是一个未曾预料到的转换,原本想一个一个命题联袂而出,命题9,10,11.﹍﹍等等。但关于“相同”的一些经典描述突然间跳入脑际,让我从莱布尼兹一下子想到了古希腊。几何原本的公理,还有亚里士多德的工具论,如同智慧精灵般,从天际之外飘落我心,落进我对莱布尼兹命题9的思绪之中。
思考莱布尼兹普遍演算中的“相同”观,把我带回到欧几里得的《几何原本》,你再从欧几里得的希腊时代回望亚里士多德。你会发现,莱布尼兹这个普遍语句演算的逻辑加,原来有它深深的古希腊之根。
命题1:若A=B,那么B=A
如果任意物和另一物相同,那么,另一物也和那个任意物相同。
证明:
1.因为A=B,(依据假设真)
2.那就可以推出,陈述A=B中的B可以用A来替换,同理,陈述A=B中的A可以用B来替换。(根据定义1,相同的定义)
所以,我们有B=A
证毕。
我们跨过有关相同和逻辑加的前8个命题证明,来看有辅助图形的命题9。片断20定义6之下,从命题5开始,全都是关于逻辑加的一类命题,从命题9开始,文字证明之后,总带有图形辅证。
命题9:如果A=B,那么A⊕C=B⊕C。
如果互为相同的两个词项,逻辑加上同样的词项,结果依然相同。
证明:
1.A⊕C=A⊕C。(依据自身同一法则)
2.A=B。(依据已知假设)
3.所以我们可以用B替换等式1.中右边的A。(依据定义1)
由此我们有:
A⊕C=B⊕C
证毕。
使用文字的例子来说明命题9的证明:
A表示词项“三角形”,B表示词项“三边形”,C表示词项“等边形”,
自然“等边三角形=等角三角形”
使用几何图形来说明命题9的证明: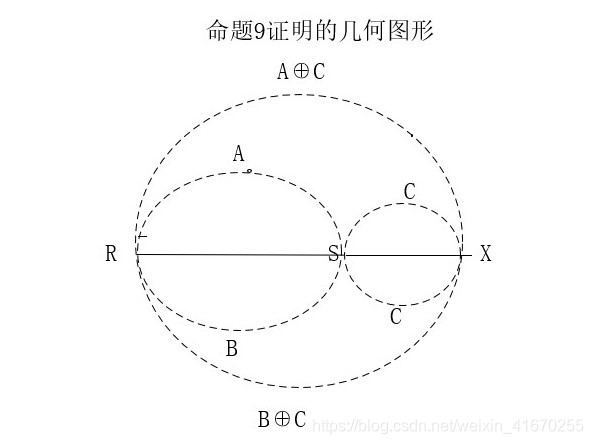
RS线段可以表示为A,也可以表示为B,自然,增加同样的线段SX=C,形成的线段RX就既是A⊕C,也是B⊕C。也就是:
A⊕C=B⊕C
把莱布尼兹的这个逻辑加命题证明和几何原本相比较,它不就是《几何原本》第一卷中那个公理2的继承么?
原本中的“公理2:等量加等量,其和仍相等。”(《几何原本》李采菊中译本第3页)
这个几何原本中的公理2,简直就是说明命题9成立的公理。
所以,从莱布尼兹的逻辑加法中,我们非常明显地看到《几何原本》的影子。
继续回溯到亚里士多德,在亚里士多德《工具论》的《论题篇》第一卷第七章,亚里士多德专门讨论到“相同”。
亚里士多德的在《论题篇》讨论词项的定义时指出,要给这些被定义的词项勾画出问题的分野,把词项自然地归属于某些特殊部门或者说某些种类。接着,他就谈到了相同:
“首先,我们要明确‘相同’这个词具有几种意义。大致地说:一般被认为有三种意义,即从数目方面或特殊方面或种类方面去使用这个名辞。所谓从数目方面,是指只有一个事物但名辞众多的情况,例如‘紧身上衣’和‘披风’,所谓从特殊方面,是指一个以上事物,但它们在种的方面没有区别,如一个人和另一个人,或一匹马和另一匹马:象这样属于同一种的,就叫做‘特殊方面相同’。同样地,那些属于同一类的事物,叫做‘种类方面相同’,比如马和人。”(《工具论.论题篇》,李匡武中译本第271-272页)
这个称作“相同”的词项,在亚里士多德那里,给它予以了词义分析,亚里士多德如此之早的首先指出“相同”的数量特性,大概能够表明亚氏所在的那个时代,人们对于数学的看重。而其后出现的《几何原本》,则在对“相同”的理解上提升到几何公理的位置,该公理的“等量”不就是从数目角度来看“相同”的么?而显然一点的是,几何原本中的这个公理2,等量加等量,其和仍相等,这里的加法指谓的只能是算术加。
这两位智者关于相同的思考和结论,一个可能的猜测也许成立。莱布尼兹在欧几里得的著作里理解到这种有关“数量相同”的算术加,又在亚里士多德那里理解到有关“词项相同”的数目意义,从而产生“逻辑加”这样一种迁延性地创新,这同时也在预示着,一个新的逻辑,不同于亚里士多德的逻辑,在17世纪就出现了雏形。2019/11/25
来源:CSDN
作者:weixin_41670255
链接:https://blog.csdn.net/weixin_41670255/article/details/103241084