正文共：1977 字 45 图 预计阅读时间： 5 分钟
前文推送
24. 特征值的应用
24.1 课程内容：马尔可夫矩阵和傅里叶级数
24.1.1 马尔科夫矩阵
马尔科夫矩阵（Markov Matrices）的定义：
矩阵中的所有元素大于 0 且 小于等于 1
各列的元素相加之和为 1 （也有一些教材用行之和为 1 ）
可以发现，马尔科夫矩阵的幂次依然是马尔科夫矩阵
马尔科夫矩阵的稳态问题就是有关特征值为 1 的对应特征向量，并且其他的特征值的绝对值都是小于 1 （可有其他特征值也为 1 的例外）。为什么呢？
由前几讲的内容我们已经知道了如下等式
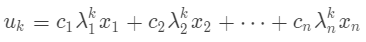
当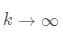 
, 因为其他特征值绝对值小于 1
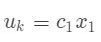
如何证明马尔科夫矩阵必然有一个特征值为 1 ？
由于列值相加为零，我们可以得到行向量线性相关，即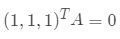 
因此矩阵 
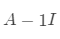奇异,所以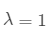 
是一个解。
同时也引出一个性质，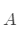
与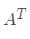 
有相同的特征值
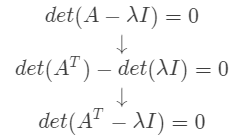
这里需要说明下马尔科夫性，马尔科夫过程和马尔科夫链。
在已知目前状态（现在）的条件下，它未来的演变（将来），不依赖于它以往的演变（过去）。这种已知“现在”的条件下，“将来”与“过去”独立的特性称为马尔科夫性，具有这种性质的随机过程为马尔科夫过程。对于离散时间的随机过程则称为马尔科夫链。
有了这些基础知识，就可以将马尔科夫矩阵应用起来了。
举个例子，将其应用于人口迁移之上。
当然我们不考虑人口总数的变化，也就是说假设人口总数不变。
只考虑两个州的人口之间的互相迁移，M 州人口 0.9 的概率留在本州，0.1 的概率迁移到 T 州，而 T 州有 0.8 的概率留在本州，0.2 概率迁移到 M 州。
由此我们得到马尔科夫转移矩阵
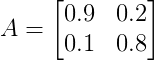
假设初始情况下两州人口分别为 0 和 1000, 则初始值为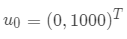 
根据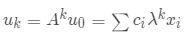 
，我们就可以知道 
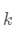步之后的人口分布。
计算特征值和特征向量，特征值为 1 和 0.7 ，对应的特征向量为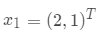 
,
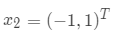, 代入初始值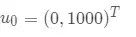 
可知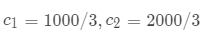 
,即得到
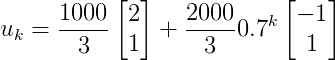
最终的稳态就是只与 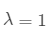所对应的 
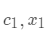相关了。
24.1.2 傅里叶级数
在讲傅里叶级数之前可以回顾下第十七讲所讲解的投影的内容，傅里叶级数正是对投影矩阵的巧妙应用。
对于一组标准正交基，我们知道它们的线性组合可以张成任意一个在此空间中的向量
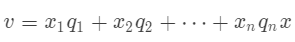
我们已经知道第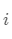 
个分量就是第 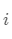个标准正交向量与 
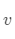的点积，即
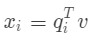
现在可以将这些概念由向量引申到函数，也即是傅里叶级数了。
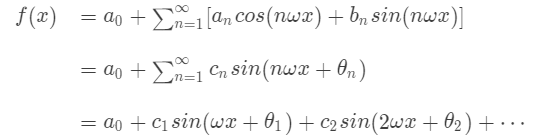
向量就对应于函数，正交向量就对应于正交函数，我们已经知道对于向量的正交，我们用两者之间的点积为 0 来定义，那么函数之间的正交如何定义？也是使用类似的方法，只不过对于连续的函数，我们使用积分来表征两者之间的内积。比如，对于两个函数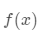 
和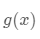 
，他们的内积表示为
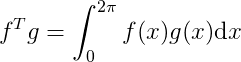
那么和正交矩阵类似的，我们想要求傅里叶级数的第 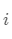项的系数的时候，也自然是用第 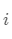项的函数与傅里叶级数做内积了，以第 1 项为例(根据第一行的等式展开)，也就是
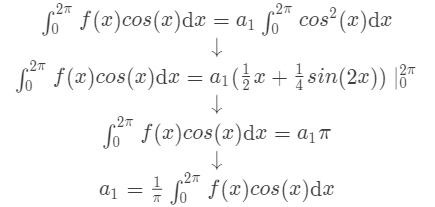
24.2 习题课
2011年将随机游走问题用马尔科夫矩阵表示习题课
（http://open.163.com/movie/2016/4/4/5/MBKJ0DQ52_MBPT38M45.html）
对于一个随机运动的粒子，在某一时刻它停留在 A 处的概率是 0.6 ，从 A 运动到 B 的概率为 0.4 ，从 B 运动到 A 的概率为 0.2 ，停留在 B 的概率为 0.8 ，问从 A 开始，粒子运动 1 步，n 步 ，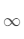
步后在 A ，B 处的概率分别为多少？
解答
首先根据运动概率，写出马尔科夫矩阵
又由于粒子是从 A 处开始运动，因此可以知道初始条件为
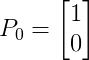
由此就可以得到运动 1 步之后在各处的概率
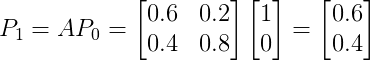
即 1 步之后粒子在 A 处的概率为 0.6 ，在 B 处的概率为 0.4 。
对于 n 步之后，我们也很容易知道其计算方法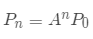 
，对于矩阵的幂，在之前的章节已经讲解过，可以对矩阵进行对角化，因此，我们计算其特征向量和特征值。 因为是马尔科夫矩阵，因此其中一个特征值为 1 ，又根据矩阵的迹为 1.4 可知另一个特征值为 0.4 。分别计算特征向量
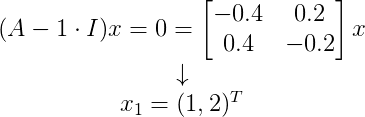
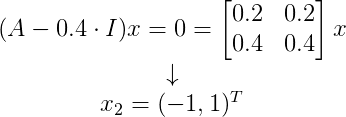
由此我们得到特征向量矩阵以及其逆和特征值矩阵分别为
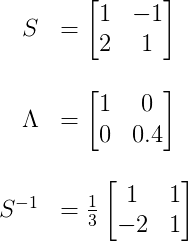
由此可以代入对角化公式得到
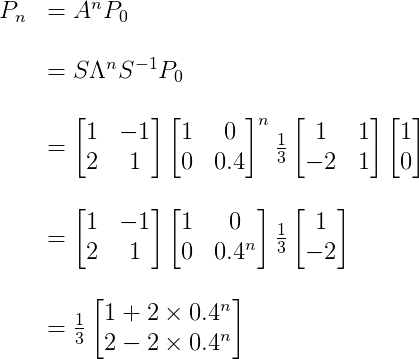
则，当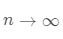 
零维领域，由内而外深入机器学习
dive into machine learning
微信号：零维领域
英文ID：lingweilingyu
本文分享自微信公众号 - 零维领域（lingweilingyu）。
如有侵权，请联系 support@oschina.cn 删除。
本文参与“OSC源创计划”，欢迎正在阅读的你也加入，一起分享。
来源：oschina
链接：https://my.oschina.net/u/4582359/blog/4384859