| 项目 | 内容 |
|---|---|
| 这个作业属于哪个课程 | 班级博客 |
| 这个作业的要求在哪里 | 作业要求 |
| 我在这个课程的目标是 | 熟悉敏捷开发,提升多人协作技能 |
| 这个作业在哪个具体方面帮助我实现目标 | 阅读《构建之法》,初步认识软件工程 |
| 教学班级 | 005 |
| 项目地址 | https://github.com/yorkyer/IntersectionProject.git |
PSP
| PSP2.1 | Personal Software Process Stages | 预估耗时(分钟) | 实际耗时(分钟) |
|---|---|---|---|
| Planning | 计划 | ||
| - Estimate | - 估计这个任务需要多少时间 | 30 | 20 |
| Development | 开发 | ||
| - Analysis | - 需求分析(包括学习新技术) | 30 | 20 |
| - Design Spec | - 生成设计文档 | 10 | 5 |
| - Design Review | - 设计复审(和同事审核设计文档) | 10 | 5 |
| - Coding Standard | - 代码规范(为目前的开发制定合适的规范) | 10 | 5 |
| - Design | - 具体设计 | 20 | 10 |
| - Coding | - 具体编码 | 60 | 120 |
| - Code Review | - 代码复审 | ||
| - Test | - 测试(自我测试,修改代码,提交修改) | 20 | 30 |
| Reporting | 报告 | ||
| - Test Report | - 测试报告 | 30 | 15 |
| - Size Measurement | - 计算工作量 | 10 | 10 |
| - Postmortem & Process Improvement Plan | - 事后总结,并提出过程改进计划 | 30 | 15 |
| 合计 | 260 | 245 |
解题思路
刚看到这个题目时联想到了计算几何的基本问题:Line Segment Intersection。令人失望的是,更加熟悉这个题目后,发现它们之间并没有关系。
容易知道,这个题有$O(n^2)$的暴力解法。但是想到 Line Segment Intersection 有更快的解法,于是探求更快的算法。
设想了一个逐步构造的方法:
假设已有 $n$ 条直线,且形成了 $m$ 个交点,每个交点所在直线的数目分别为$t_i$, 现有第 $n+1$ 条不同于前 $n$ 条的直线。若其与其他 $l$ 条直线平行,且第 $k_1,k_2,\cdots,k_h$ 个交点在该直线上,则新形成的交点数为:
$$
n-l-\sum_{i=1}^{h} t_{k_i}
$$
从而总交点个数为:$m+n-l-\sum_{i=1}^{h} t_{k_i}$然而经过进一步的思考,发现上述算法的实现依然是 $O(n^2)$ 的。
最终回归暴力解法,算出每一对几何图形的交点,然后去重。
设计实现过程
数据结构
因为本项目的任务比较简单,故没有用类来表示几何对象,而是用大小为4的向量表示直线,大小为3的向量表示圆。
算法
关键函数有三个,分别是计算直线与直线、直线与圆、圆与圆的交点的函数。其中计算圆与圆的交点时利用了计算直线与圆的函数。令有一个辅助函数来统一上述三个函数。
单元测试覆盖了关键函数的各种情况,包括直线与直线的平行与相交,直线与圆的相离、相切与相交,圆与圆的相交、相切与相离。
对交点的去重利用了
set数据结构。
性能改进
- 性能分析图
代码说明
数学公式来源于维基百科。
计算直线与直线相交的函数

计算直线与圆相交的函数

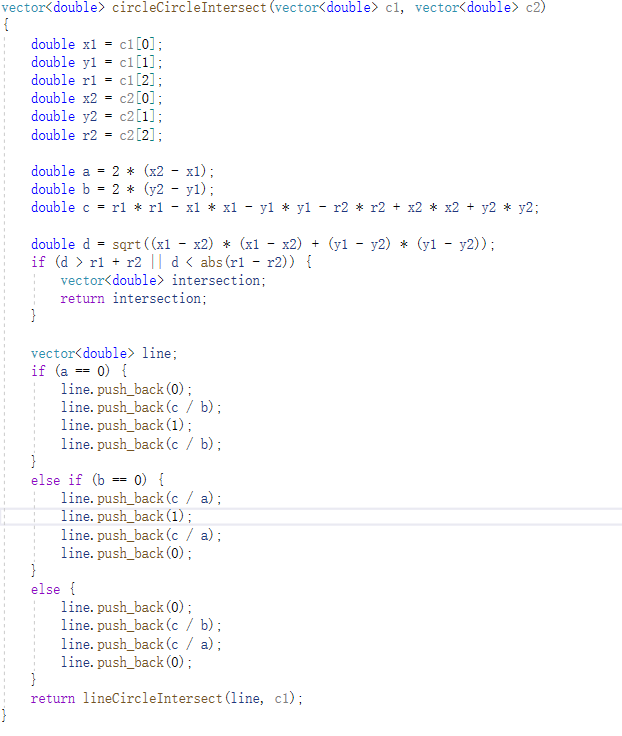
计算圆与圆相交的函数

来源:https://www.cnblogs.com/yorkyer/p/12457427.html