卡特兰数

katalan

 

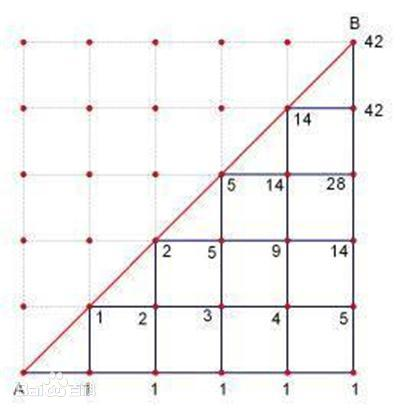
 H(n)h(n)表示，从原点出发，每次向x或y轴正方向移动1单位，到达点(n,n)，且在移动过程中不越过第一象限平分线的移动方案数。

h(n)= h(0)*h(n-1)+h(1)*h(n-2) + ... + h(n-1)*h(0) (n>=2)

h(0)=1 ,h(1)=1

简化为h(n)=c(2n,n)-c(2n,n+1)(n=0,1,2,…)

 

卡特兰数的应用

1.像上面这样的正方形格子，只能走下半边，求能走的方式有多少种

引申：如果能把这个格子走的形式看作+1，-1

+1代表向上   -1代表向右

那么凡是可以这样表示的东西都可以用卡特兰数

比如  括号匹配   能有多少种方法 等这类出栈入栈问题

2.凸多边形三角划分

先任意选两个基边  再从其他点任意选一个点  

再无限划分

3.再有就是二叉树  

但是我不太会🤭

参考以下博客

https://blog.csdn.net/qq_43731019/article/details/99624344

来源：https://www.cnblogs.com/AAAzhuo/p/12233846.html