20182320 2019-2020-1 《数据结构与面向对象程序设计》实验8报告
课程:《程序设计与数据结构》
班级: 1823
姓名: 郑力元
学号:20182320
实验教师:王志强
实验日期:2019年11月11日
必修/选修: 必修
1.实验内容
1.1
参考教材PP16.1,完成链树LinkedBinaryTree的实现(getRight,contains,toString,preorder,postorder)
用JUnit或自己编写驱动类对自己实现的LinkedBinaryTree进行测试,提交测试代码运行截图,要全屏,包含自己的学号信息
课下把代码推送到代码托管平台
1.2
基于LinkedBinaryTree,实现基于(中序,先序)序列构造唯一一棵二㕚树的功能,比如给出中序HDIBEMJNAFCKGL和后序ABDHIEJMNCFGKL,构造出附图中的树
用JUnit或自己编写驱动类对自己实现的功能进行测试,提交测试代码运行截图,要全屏,包含自己的学号信息
课下把代码推送到代码托管平台
1.3
自己设计并实现一颗决策树
提交测试代码运行截图,要全屏,包含自己的学号信息
课下把代码推送到代码托管平台
1.4
输入中缀表达式,使用树将中缀表达式转换为后缀表达式,并输出后缀表达式和计算结果(如果没有用树,正常评分。如果用到了树,即使有小的问题,也酌情给满分)
提交测试代码运行截图,要全屏,包含自己的学号信息
2. 实验过程及结果
2.1
第一步:补充实现书上的LinkedBinaryTree类,它需要编写一个BinaryTree接口,一个节点类,两个异常类,才能完整实现LinkedBinaryTree。
代码如下,这里将书上的ArrayIterator换成了ArrayList:
public class LinkedBinaryTree<T> implements BinaryTree<T>
{
protected BTNode<T> root;
public LinkedBinaryTree()
{
root = null;
}
public LinkedBinaryTree (T element)
{
root = new BTNode<T>(element);
}
public LinkedBinaryTree (T element, LinkedBinaryTree<T> left,
LinkedBinaryTree<T> right)
{
root = new BTNode<T>(element);
root.setLeft(left.root);
root.setRight(right.root);
}
public T getRootElement() throws Exception, EmptyCollectionException {
if (root == null)
throw new EmptyCollectionException ("Get root operation "
+ "failed. The tree is empty.");
return root.getElement();
}
public LinkedBinaryTree<T> getLeft() throws Exception, EmptyCollectionException {
if (root == null)
throw new EmptyCollectionException ("Get left operation "
+ "failed. The tree is empty.");
LinkedBinaryTree<T> result = new LinkedBinaryTree<T>();
result.root = root.getLeft();
return result;
}
public T find (T target) throws ElementNotFoundException {
BTNode<T> node = null;
if (root != null)
node = root.find(target);
if (node == null)
throw new ElementNotFoundException("Find operation failed. "
+ "No such element in tree.");
return node.getElement();
}
//返回大小
public int size()
{
int result = 0;
if (root != null)
result = root.count();
return result;
}
public LinkedBinaryTree<T> getRight() throws Exception, EmptyCollectionException {
if (root == null)
throw new EmptyCollectionException ("Get left operation "
+ "failed. The tree is empty.");
LinkedBinaryTree<T> result = new LinkedBinaryTree<T>();
result.root = root.getRight();
return result;
}
public boolean contains (T target) {
if (root.find(target)==null){
return false;
}
else {
return true;
}
}
public boolean isEmpty() {
if (root==null){
return true;
}
else {
return false;
}
}
//先序遍历
public ArrayList<T> preorder() {
ArrayList<T> iter = new ArrayList<T>();
if (root != null)
root.preorder (iter);
return iter;
}
//后续遍历
public ArrayList<T> postorder() {
ArrayList<T> iter = new ArrayList<T>();
if (root != null)
root.postorder (iter);
return iter;
}
public String toString() {
return super.toString();
}
}
第二步:编写测试代码,运行
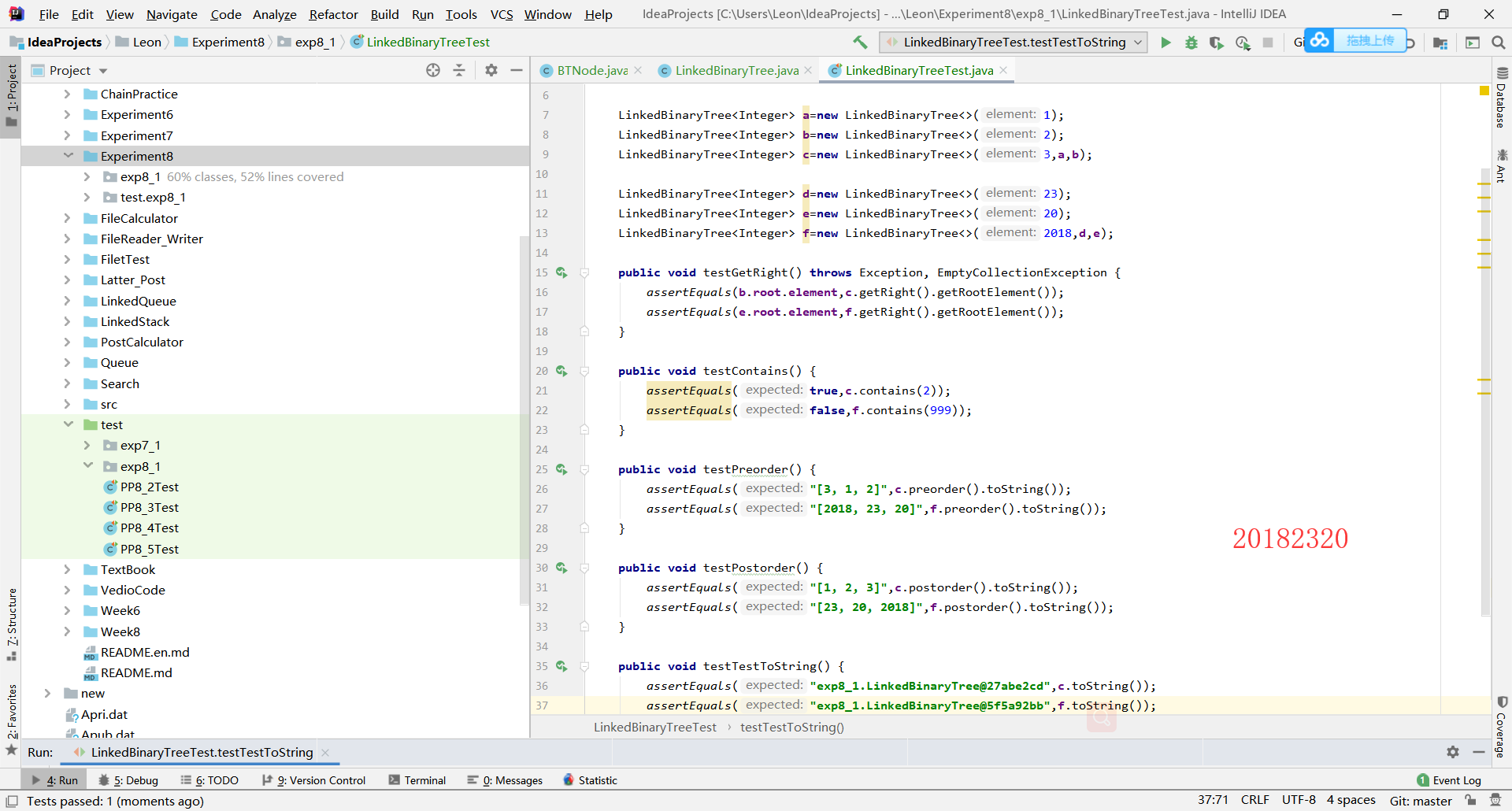
2.2
第一步:修改上面的LinkedBinaryTree方法,将先序、中序和后序遍历都改成返回字符串,同时加入能够从上到下构造二叉树的方法:
public int findIndexInArray(char[] a, char x, int begin, int end) {
for(int i=begin;i<=end;i++) {
if(a[i] == x) {
return i;
}
}
return -1;
}
public void initTree(char[] preOrder, char[] inOrder) {
this.root = this.initTree(preOrder, 0, preOrder.length-1, inOrder, 0, inOrder.length-1);
}
public BTNode initTree(char[] preOrder, int start1, int end1, char[] inOrder, int start2, int end2) {
if(start1 > end1 || start2 > end2) {
return null;
}
//通过前序找到根结底
char rootData = preOrder[start1];
BTNode<Character> head = new BTNode(rootData);
//从中序遍历里找到根结点所在的位置
int rootIndex = findIndexInArray(inOrder, rootData, start2, end2);
//offSet代表左子树的长度-1(也就是中序遍历中,左子树最后一个元素的下标)
int offSet = rootIndex - start2 - 1;
//递归构建左子树
BTNode left = initTree(preOrder, start1+1, start1+1+offSet, inOrder, start2, start2+offSet);
//递归构建右子树
BTNode right = initTree(preOrder, start1+offSet+2, end1, inOrder, rootIndex+1, end2);
head.left = left;
head.right = right;
return head;
}
第二步:编写测试代码,运行,这里用后续遍历检验是否正常构建二叉树

2.3
第一步:编写好节点类和决策树类(包含主方法和构建与运行决策树的方法)
public static void buildDTree(){
root=new BTNode("大力帅吗?y/n");
BTNode<String> temp=root;
temp.left=new BTNode<>("你错了。");
temp.right=new BTNode<>("大力聪明吗?y/n");
temp=temp.right;
temp.left=new BTNode<>("你错了。");
temp.right=new BTNode<>("大力强吗?y/n");
temp=temp.right;
temp.left=new BTNode<>("你错了。");
temp.right=new BTNode<>("你说的都对了。");
}
public static void runDTree(BTNode root){
System.out.println(root.element);
if (root.left==null||root.right==null){
return;
}
while (true){
stringTokenizer=new StringTokenizer(scanner.nextLine());
String string=stringTokenizer.nextToken();
if (string.equals("y")){
runDTree(root.right);
break;
}
else if (string.equals("n")){
runDTree(root.left);
break;
}
else {
System.out.println("输入错误!重新输入。");
}
}
}
第二步:运行
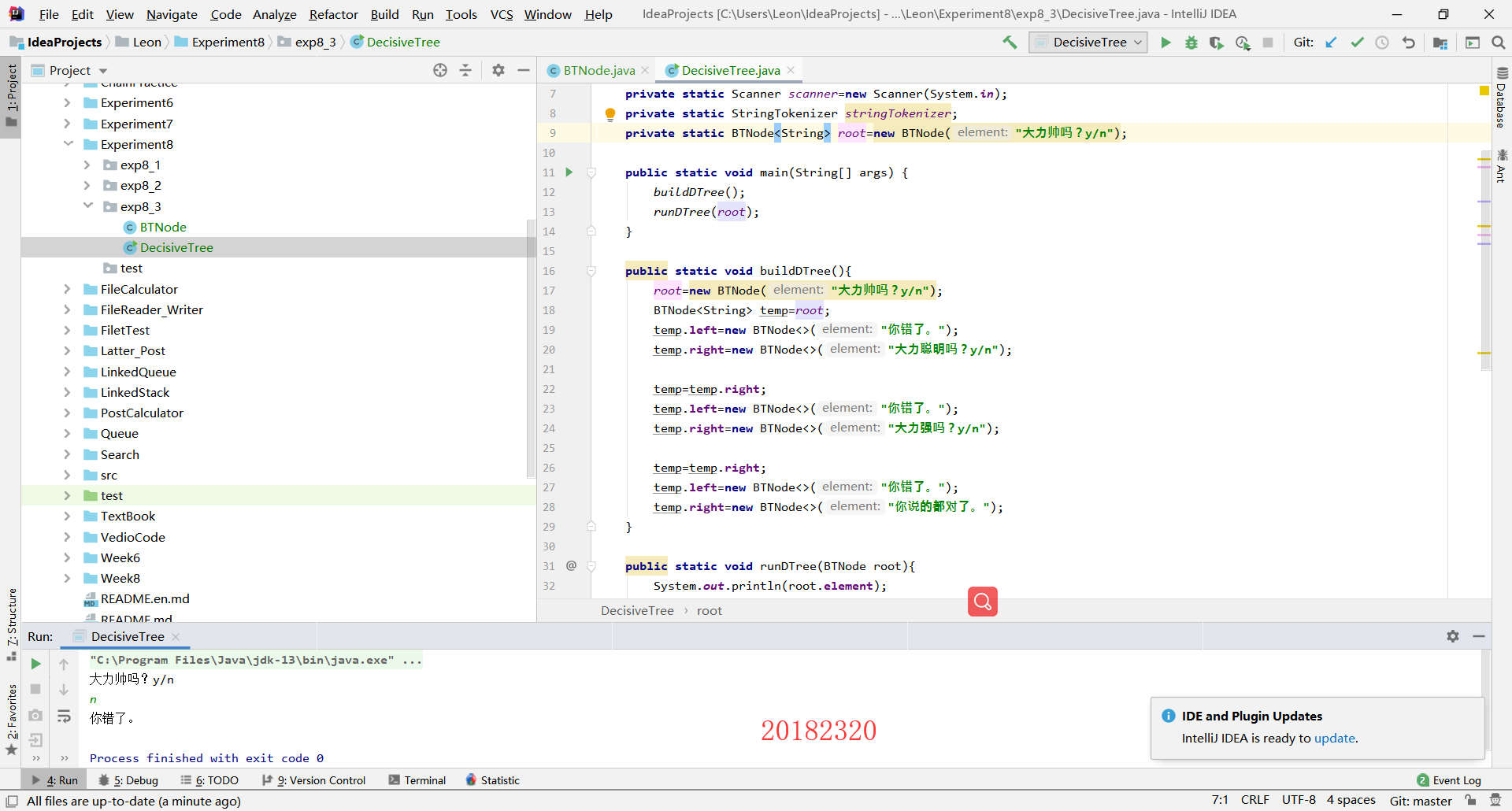
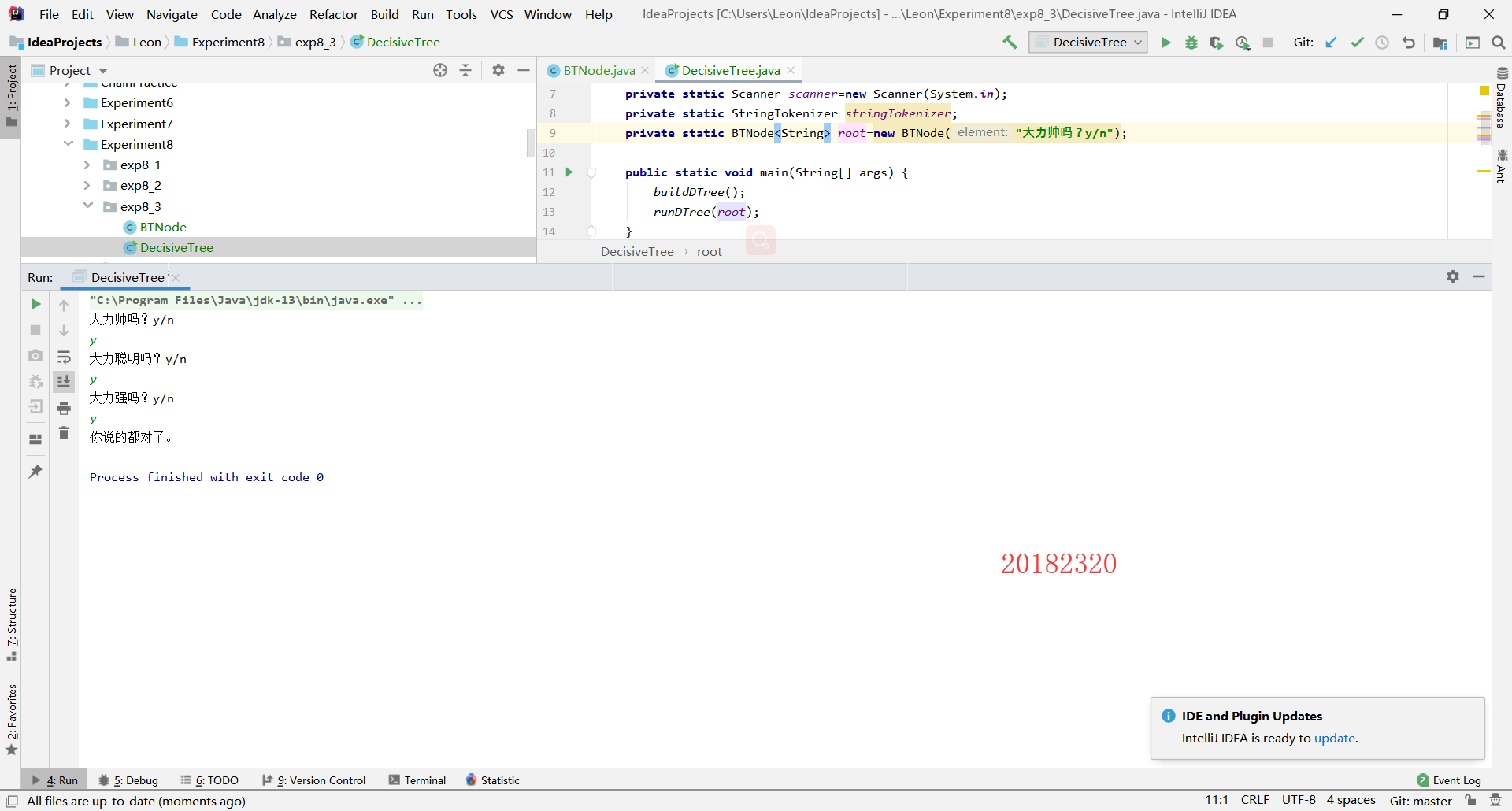
2.4
第一步:编写中缀转后缀的类(包括主方法):
public static String infixToSuffix(String infix) {
Stack<Character> stack = new Stack<Character>();
String suffix = "";
int length = infix.length();
for (int i = 0; i < length; i++) {
Character temp;
char c = infix.charAt(i);
switch (c) {
// 忽略空格
case ' ':
break;
// 碰到'(',push到栈
case '(':
stack.push(c);
break;
// 碰到'+''-',将栈中所有运算符弹出,送到输出队列中
case '+':
case '-':
while (stack.size() != 0) {
temp = stack.pop();
if (temp == '(') {
stack.push('(');
break;
}
suffix += " " + temp;
}
stack.push(c);
suffix += " ";
break;
// 碰到'*''/',将栈中所有乘除运算符弹出,送到输出队列中
case '*':
case '/':
while (stack.size() != 0) {
temp = stack.pop();
if (temp == '(' || temp == '+' || temp == '-') {
stack.push(temp);
break;
} else {
suffix += " " + temp;
}
}
stack.push(c);
suffix += " ";
break;
// 碰到右括号,将靠近栈顶的第一个左括号上面的运算符全部依次弹出,送至输出队列后,再丢弃左括号
case ')':
while (stack.size() != 0) {
temp = stack.pop();
if (temp == '(')
break;
else
suffix += " " + temp;
}
// suffix += " ";
break;
//如果是数字,直接送至输出序列
default:
suffix += c;
}
}
//如果栈不为空,把剩余的运算符依次弹出,送至输出序列。
while (stack.size() != 0) {
suffix += " " + stack.pop();
}
return suffix;
}
第二步:运行
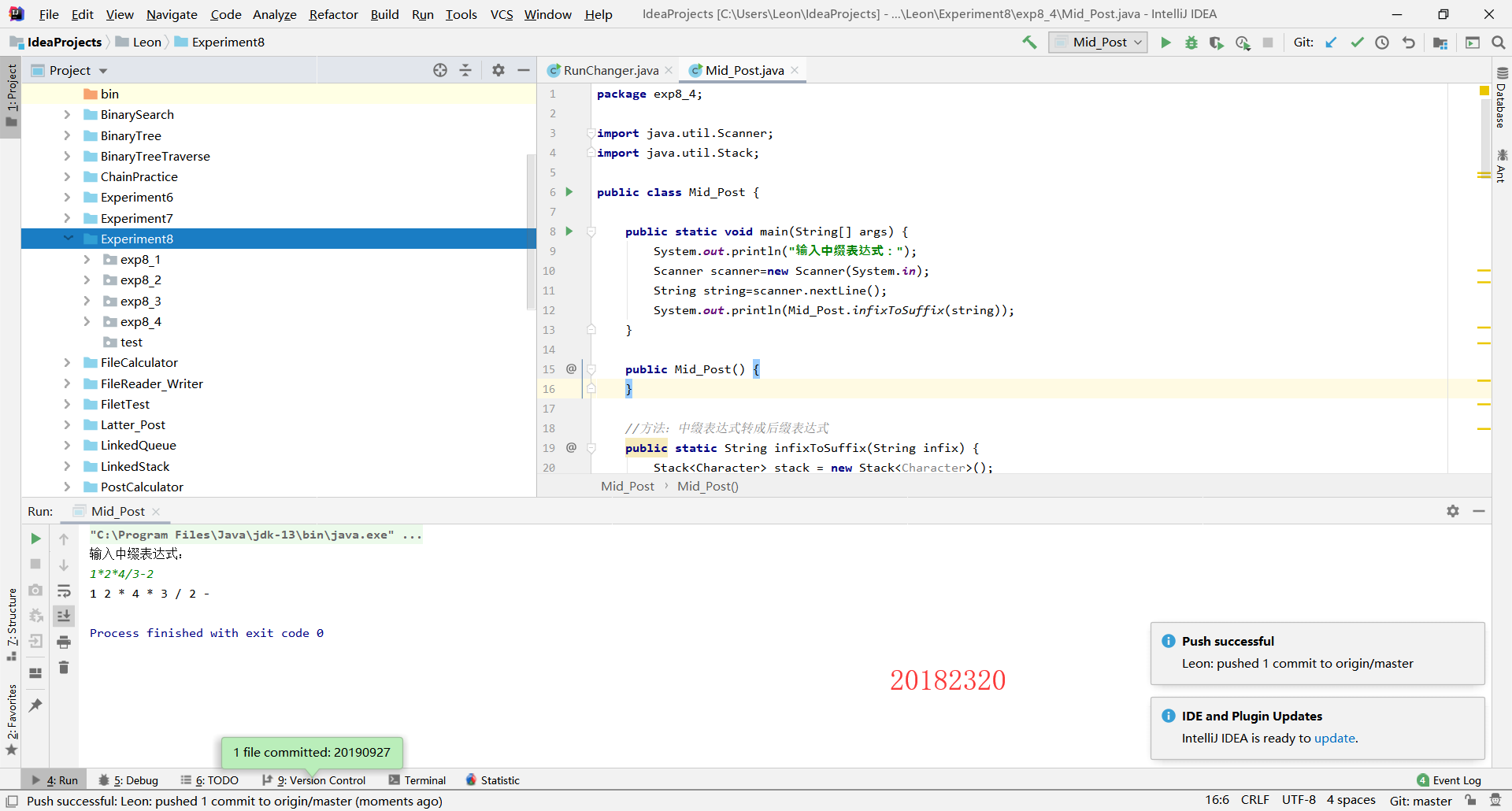
3. 实验过程中遇到的问题和解决过程
问题1:
原本是想基于LinkedBinaryTree的构造二叉树的方法,完成8.2的二叉树的构建,但是发现LinkedBinaryTree的原本构造方法是自下而上构造二叉树的,然而已知的先序和中序遍历能确定的根是在二叉树的最顶端
问题1解决:
自己加了一个自上而下的构造二叉树的方法,实现功能。
其他(感悟、思考等)
这一次实验主要考察我们对树的结构以及其特点的掌握,涉及到了树的构建、通过前序与中序构造树还有决策树的构建。虽然在最后一个中缀转后缀中我没能用树的结构来实现,但是通过栈和队列两种线性结构来实现这个功能难度依然不小,花费时间较多。这些编程实践能够让我们对一些经典的数据结构有更深刻的理解。