字典树基础知识学习笔记

节点最多有N个时，开一个二维数组son[N][M]（M为所有字符的总个数），记录每个点的儿子。对每一个字符串的结尾的序号，用cnt[N] 数组来记录有多少个这样的字符串，这张图可以帮助理解：

假设给定的字符串（只由a, b, c, d组成）为：aabc, aabd, aabd, cdb, cdba

son[i][4] 就是第i个节点下面的4个格子

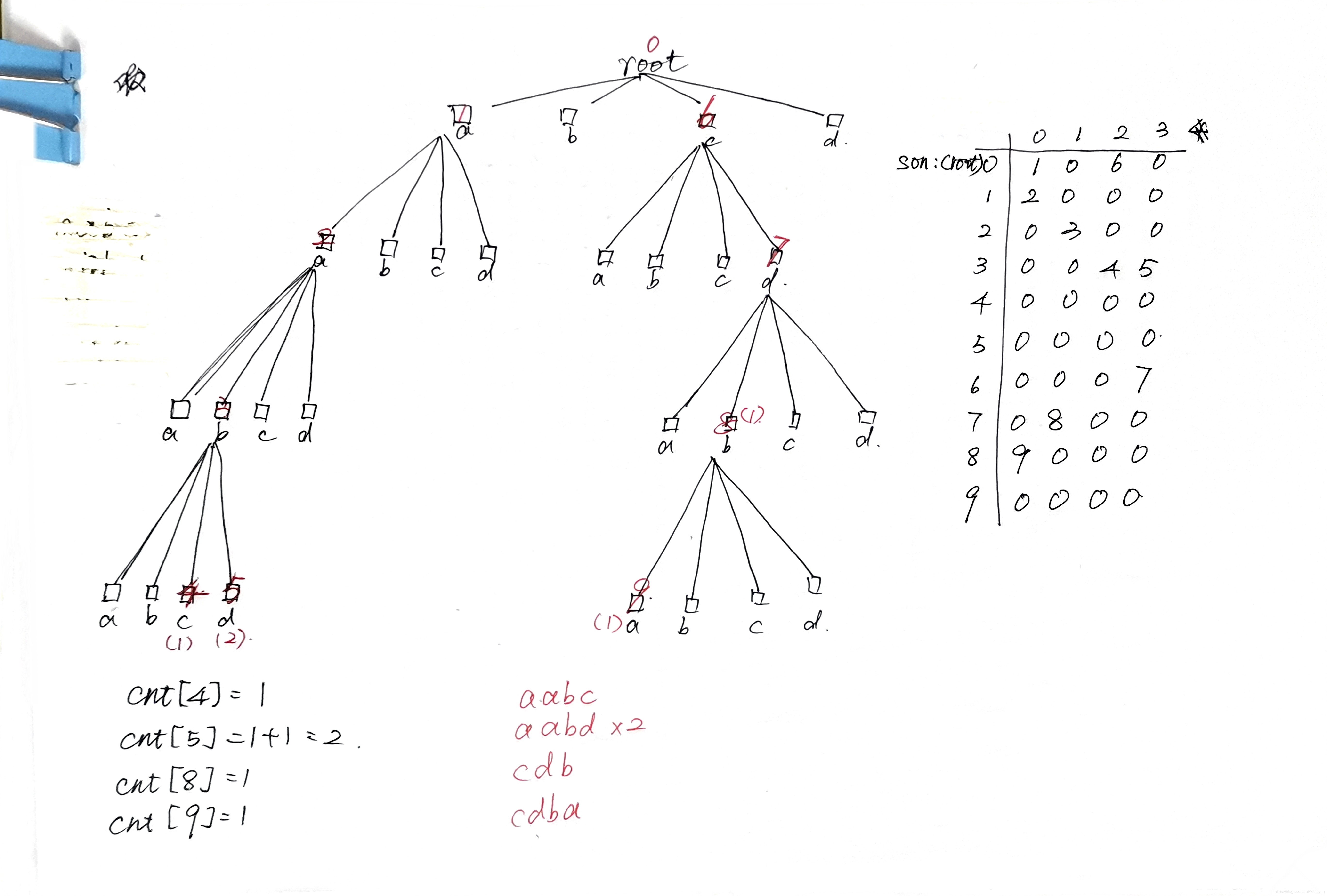
下面附两道模板题：

1.https://www.acwing.com/problem/content/837/

#include <iostream>
#include <cstdio>
#include <cstring>
#define N 100010
using namespace std;

int son[N][26], cnt[N], idx;
int n;

void insert(string str)
{
	int p = 0; // 每次插入都从root节点开始
	for (int i = 0; i < str.size(); i ++)
	{
		int u = str[i] - 'a'; // 找到属于这个节点的对应的格子
		if(!son[p][u]) son[p][u] = ++ idx; // 如果这个格子是空的，就把它标记上序号
		p = son[p][u]; // 然后走到这个格子上
	}
	// 现在已经走到了这个字符串的结尾的字符（不一定是叶节点）
	cnt[p] ++; // 记录这个节点代表的字符串出现的次数
}

int query(string str)
{
	int p = 0; // 每次查询也都从叶节点开始
	for (int i = 0; i < str.size(); i ++)
	{
		int u = str[i] - 'a';
		if(!son[p][u]) return 0; // 如果这个格子是空的（没有这个节点），说明没有这个字符串
		p = son[p][u]; // 如果由这个格子上有字符，就走到那里去，继续看下一个字符
	}
	return cnt[p]; // 已经走到这个字符串的结尾，输出之前标记的次数
}

int main()
{
	int n;
	cin >> n;
	while(n --)
	{
		char ch[2], str[N];
		scanf("%s%s", ch, str);
		if(*ch == 'I') insert(str);
		else printf("%d\n", query(str));
	}
	return 0;
}

 

2. https://vjudge.net/contest/352395#problem/A 升级版，更精彩🙃

#include <iostream>
#include <cstdio>
#include <cstring>
#define N 100010
#define M 10010
using namespace std;

int son[N][15], cnt[N], idx;
int n, kase;
char str[M][15];

bool insert(char str[])
{
	int p = 0;
	for (int i = 0; str[i]; i ++)
	{
		int u = str[i] - '0';
		if(cnt[son[p][u]]) return false;
		if(!son[p][u]) son[p][u] = ++ idx;
		p = son[p][u];
	}

	cnt[p] ++;
	return true;
}

bool find(char str[])
{
	int p = 0;
	for (int i = 0; i < strlen(str) - 1; i ++) // 开始的判断条件写的是 str[i]，wa哭了，每次都因为搜到了自己返回true😂
	{
		int u = str[i] - '0';
		if(cnt[son[p][u]]) return true;// 如果这个节点已经被标记为结尾了，就返回true
		p = son[p][u];
	}
	return false;
}


int main()
{
	cin >> kase;
	while(kase --)
	{
		bool isok = true;
		idx = 0;
		memset(son, 0, sizeof son);
		memset(cnt, 0, sizeof cnt);

		scanf("%d", &n);

		for (int i = 0; i < n; i ++) // 先正着来一遍
		{
			scanf("%s", str[i]);
			if(!insert(str[i]) && isok)
			{
				isok = false;
				continue;
			}
		}

		if(n == 1)
		{
			puts("YES");
			continue;
		}

		if(!isok)
		{
			puts("NO");
			continue;
		}

		for (int i = n - 1; i >= 0; i --) // 如果正着可以再反着看一遍（开始没有看后面的数是否为前面的前缀waqwq）
		{
			if(find(str[i]))
			{
				isok = false;
				break;
			}
		}

		if(!isok)
		{
			puts("NO");
		}
		else puts("YES");
	}
	return 0;
}

 

 

来源：CSDN

作者：Victayria

链接：https://blog.csdn.net/Victayria/article/details/104211603