并查集
简介
并查集,在一些有N个元素的集合应用问题中,我们通常是在开始时让每个元素构成一个单元素的集合,然后按一定顺序将属于同一组的元素所在的集合合并,其间要反复查找一个元素在哪个集合中。这一类问题近几年来反复出现在信息学的国际国内赛题中,其特点是看似并不复杂,但数据量极大,若用正常的数据结构来描述的话,往往在空间上过大,计算机无法承受;即使在空间上勉强通过,运行的时间复杂度也极高,根本就不可能在比赛规定的运行时间(1~3秒)内计算出试题需要的结果,只能用并查集来描述。
并查集是一种树型的数据结构,用于处理一些不相交集合(Disjoint Sets)的合并及查询问题。常常在使用中以森林来表示。(转自百度百科)
主要操作
众所周知,每个学校都有些奇怪的组织,有些是学校的,还有些''地下党''(咳咳,懂得),然后每个组织又分为了几个小组........当每年开学的那一天。总有些新面孔会来到这些组织,但是显然暂时不会。,这就意味着他们不属于任何一个组织

初始化
for(int i=1;i<=n;i++)
f[i]=i;
几个月后,这些新同学陆陆续续的加入了组织,有一天,学校让所有的组织集合,这下好了,因为是新同学,所以他们只记得自己的上级,所以只能去找上级,好巧不巧,上级也只认识自己的上级(????)最后一大堆人浩浩荡荡地找到了组织长,愉快地集合了起来
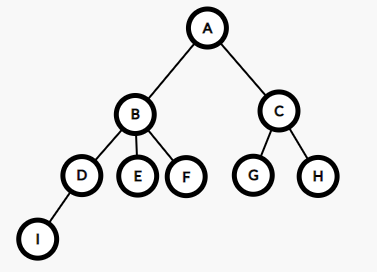
查找
int get(int x)
{
if(f[x]==x)return x;//找到根节点
return get(f[x]);//不然就继续向上找
}
然而这些人的智商也不算低,记住了自己的组织长,下次集合直接找自己的组织长就可以了,不用麻烦的走一趟了。
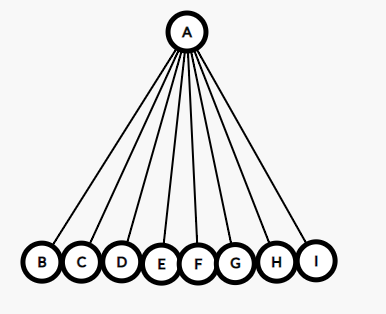
路径压缩
int get(int x)
{
if(f[x]==x)return x;//找到根节点
return f[x]=get(f[x]);//不然就继续向上找,然后记录
}
然后,学校嫌组织过多,要合并一些组织了,然后把XX部和OO部合并在了一起,但是一个部得有一个领头人啊,所以,我们决定让XX部的部长当了新的XO部的部长。这样OO部部长的上级就是XX部部长了(OO部部长:为什么不是我)
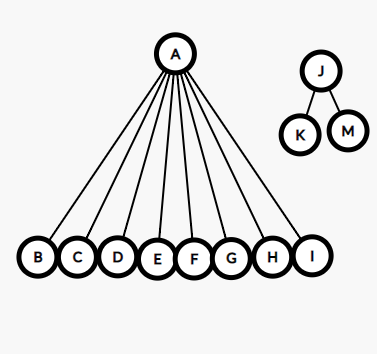
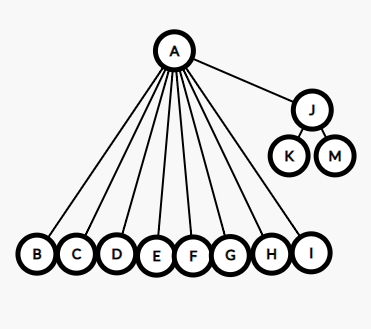
合并
void merge(int x,int y)
{
int tx=get(x);
int ty=get(y);
if(tx!=ty)//不在同一集合就合并(其实也可以不要判断,反正在同一集合合并了也不会变)
fa[tx]=ty;
return;
}
实际应用
嗯,这就是一道模板题
1 #include<bits/stdc++.h>
2 using namespace std;
3 int n,m;
4 int fa[10001];
5 int get(int x)//找根结点
6 {
7 if(fa[x]==x)return x;
8 else return fa[x]=get(fa[x]);//路径压缩
9 }
10 void merge(int x,int y)//合并
11 {
12 int tx=get(x),ty=get(y);
13 if(tx!=ty)
14 fa[tx]=ty;
15 return;
16 }
17 int main()
18 {
19 scanf("%d%d",&n,&m);
20 for(int i=1;i<=n;i++)
21 fa[i]=i;//初始化
22 while(m--)
23 {
24 int z,x,y;
25 scanf("%d%d%d",&z,&x,&y);
26 if(z==1)
27 merge(x,y);
28 else
29 {
30 if(get(x)==get(y))cout<<"Y"<<endl;
31 else cout<<"N"<<endl;
32 }
33 }
34 return 0;
35 }
带权并查集
嗯,和普通的并查集没什么区别
普通的并查集代表着集合与集合之间的关系,但是带权并查集还维护了点与点之间的关系(毕竟带权嘛)。但是上例题前,我们先来康康怎么来带权并查集的路径压缩。
查找
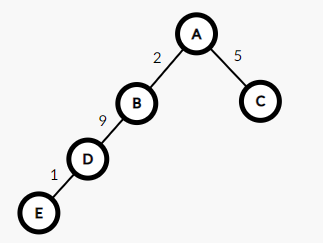
首先,这里有一个未压缩的并查集,假设查找E的根结点,我们需要E到D的距离加上D到A的距离,但是D到A的距离,又需要D到B的距离加上B到A的距离.....
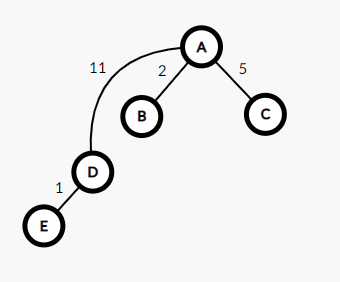
sum表示这个点到根结点的权值
1 int get(int x)
2 {
3 if(root[x]==x)return x;
4 int fa=get(root[x]);
5 sum[x]+=sum[root[x]];
6 return root[x]=fa;
7 }
注意第四行,一定要写在压缩权值的前面,以图为例,如果写在后面,那么E到A的距离会变成ED加上DB,就是E到B的距离了,然而这不是我们想要的结果,所以先找到根,然后从根结点慢慢回来,路上再更新权值,这样才是有效的。而不是从某个结点向根结点更新。
合并
首先你有两个关系
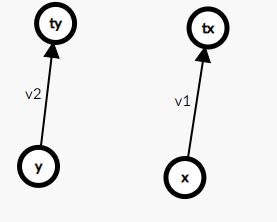
然后题目又给了你x到y的权值,现在有了这一条红线你就要合并这两个并查集了
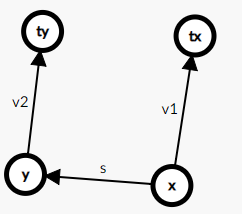
我们想把tx并到ty去,但是就必须得知道tx到ty的权值

我们不难知道,x到ty的两条线路的权值都得相同,所以只需要用v2+s-v1即可
root[tx]=ty; sum[tx]=s+sum[y]-sum[x];
嗯,看看这个题,大概就是有一串你不知道的数,每次给你一个区间的和,看是否与前面已知的重复。例如已知[2,9]=10,[2,5]=8,又给你[6,9]=3,那么显然不对,因为我们从前面可知[3,9]应该等于2(自己算的出来吧)。
但是还有一个注意的地方,我们用sum数组代表一个点到根结点的所有权值,但是初始化的时候例如sum[1]=0(此时1本身是根结点),这个代表的是[1,1]等于0,也就是a[1]到a[1]等于0.但是这样的话就表示你已经确切的知道了这个值,然而我们不知道这个值,所以不妨把闭区间的某一段变成开区间,例如[1,1]改成(0,1],这样sum[1]就代表(1,1],也不会冲突了。
1 #include<bits/stdc++.h>
2 using namespace std;
3 int n,m,ans;
4 int root[200005],sum[200005];
5 int get(int x)//查找
6 {
7 if(root[x]==x)return x;
8 int fa=get(root[x]);
9 sum[x]+=sum[root[x]];
10 return root[x]=fa;
11 }
12 int main()
13 {
14 while(~scanf("%d%d",&n,&m))
15 {
16 ans=0;
17 for(int i=0;i<=n;i++)//初始化,一定要从0开始
18 {
19 root[i]=i;
20 sum[i]=0;
21 }
22 while(m--)
23 {
24 int x,y,s;
25 scanf("%d%d%d",&x,&y,&s);
26 x--;
27 int tx=get(x);
28 int ty=get(y);
29 if(tx==ty)//如果是同一个并查集,就看是否合法即可
30 {
31 if(sum[x]-sum[y]!=s)
32 ans++;
33 }
34 else//否则合并一下
35 {
36 root[tx]=ty;
37 sum[tx]=s+sum[y]-sum[x];
38 }
39 }
40 cout<<ans;
41 }
42 return 0;
43 }
种类并查集
种类并查集,就像他的名字一样,有几个种类,就有几个区间,对应的就要开几倍数组。所谓区间,就像下面的图一样:

我们现在假设有两个种类,然后每一个数都有可能是x种类或者y种类,随之对应的,如果一个数m是x种类,那么它就是m,否则它是m+n
.再来看看例题,它有三个种类,所以我们要开三倍数组,然后首先每个数的根结点都是自己,我们现有三个种类:A,B,C,然后得到了a吃b,a有三种情况,当a为A种类时,b就为B种类,当a为B种类时,b就为C种类.......然后三个并查集分别维护,一旦发生冲突,就ans++即可
1 #include<iostream>
2 using namespace std;
3 int root[500005];
4 int n,m,ans;
5 int get(int x)//查找
6 {
7 if(root[x]==x)return x;
8 return root[x]=get(root[x]);
9 }
10 void merge(int x,int y)//合并
11 {
12 int tx=get(x);
13 int ty=get(y);
14 root[tx]=ty;
15 return;
16 }
17 int main()
18 {
19 scanf("%d%d",&n,&m);
20 for(int i=1;i<=3*n;i++)//初始化,三倍数组
21 root[i]=i;
22 while(m--)
23 {
24 int x,y,z;
25 scanf("%d%d%d",&z,&x,&y);
26 if(x>n||y>n||z==2&&x==y)ans++;//不合法
27 else if(z==1)//同一种类
28 {
29 if(get(x+n)==get(y)||get(x+2*n)==get(y))//如果他们已经有了关系并且不是同一种类,ans++
30 {
31 ans++;
32 continue;
33 }
34 merge(x,y);//都是A种
35 merge(x+n,y+n);//都是B种
36 merge(x+2*n,y+2*n);//都是C种
37 }
38 else//x吃y
39 {
40 if(get(x)==get(y)||get(x+n)==get(y))//如果他们有了关系并且是同种类或者x被y吃,ans++
41 {
42 ans++;
43 continue;
44 }
45 merge(x,y+n);//x是A种,吃为B种的y
46 merge(x+n,y+2*n);//x是B种,吃为C种的y
47 merge(x+2*n,y);//x是C种,吃为A种的y
48 }
49 }
50 cout<<ans;
51 }
然后这道题也可以用权值并查集来做,我们假设同根结点比,0是同类,1被根结点吃,2吃根结点,然后初始化是每个点都是自己的同类,和权值并查集的合并一样.但是因为这里的关系只有三种,所以当我们维护权值的时候有一个取模三的操作。如图,tx与ty的关系就是(1+0+3-2)%3=2.(然而我好像没有这样写)

1 #include<iostream>
2 using namespace std;
3 int n,m,ans;
4 struct node{
5 int root;
6 int val;//0同类,1被吃,2吃根
7 }a[50005];
8 int get(int x)
9 {
10 if(a[x].root==x)return x;
11 int y=a[x].root,z=get(y);
12 a[x].val=(a[x].val+a[y].val)%3;
13 return a[x].root=z;
14 }
15 int merge(int z,int x,int y)
16 {
17 int tx=get(x),ty=get(y);
18 if(tx==ty)//在同一集合
19 {
20 if((a[y].val+(3-a[x].val))%3!=z-1)//判断是否冲突
21 return 1;
22 }
23 else
24 {
25 a[ty].root=tx;
26 a[ty].val=((z-1)+(3-a[y].val)+a[x].val)%3;//算关系
27 }
28 return 0;
29 }
30 int main()
31 {
32 scanf("%d%d",&n,&m);
33 for(int i=1;i<=n;i++)
34 {
35 a[i].root=i;
36 a[i].val=0;
37 }
38 while(m--)
39 {
40 int x,y,z;
41 scanf("%d%d%d",&z,&x,&y);
42 if(x>n||y>n)ans++;
43 else if(z==2&&x==y)ans++;
44 else ans+=merge(z,x,y);//合并
45 }
46 cout<<ans;
47 }
其实种类并查集就是权值并查集一个特殊的存在,总而言之都是并查集就对了(滑稽)