Function to return date of Easter for the given year

Question

So, here\'s a funny little programming challenge. I was writing a quick method to determine all the market holidays for a particular year, and then I started reading about E

Answer 1

Python: using dateutil's easter() function.

>>> from dateutil.easter import *
>>> print easter(2010)
2010-04-04
>>> print easter(2011)
2011-04-24

The functions gets, as an argument, the type of calculation you like:

EASTER_JULIAN   = 1
EASTER_ORTHODOX = 2
EASTER_WESTERN  = 3

You can pick the one relevant to the US.

Reducing two days from the result would give you Good Friday:

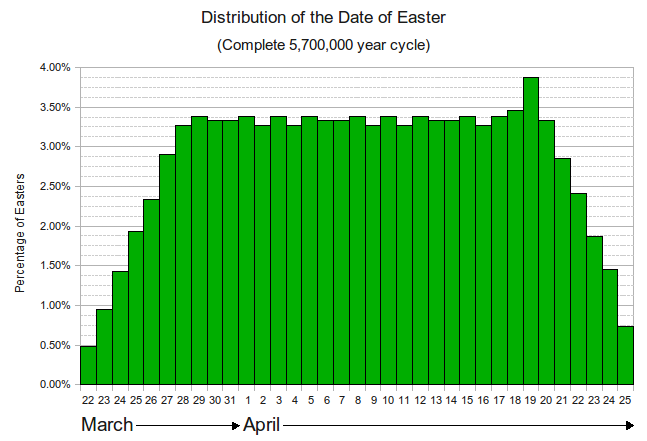
>>> from datetime import timedelta
>>> d = timedelta(days=-2)
>>> easter(2011)
datetime.date(2011, 4, 24)
>>> easter(2011)+d
datetime.date(2011, 4, 22)

Oddly enough, someone was iterating this, and published the results in Wikipedia's article about the algorithm:

Answer 2

Found this Excel formula somewhere
Assuming cell A1 contains year e.g. 2020

ROUND(DATE(A1;4;1)/7+MOD(19*MOD(A1;19)-7;30)*0,14;0)*7-6

Converted to T-SQL lead me to this:

DECLARE @yr INT=2020
SELECT DATEADD(dd, ROUND(DATEDIFF(dd, '1899-12-30', DATEFROMPARTS(@yr, 4, 1)) / 7.0 + ((19.0 * (@yr % 19) - 7) % 30) * 0.14, 0) * 7.0 - 6, -2)

Answer 3

in SQL Server Easter Sunday would look like this, scroll down for Good Friday

CREATE FUNCTION dbo.GetEasterSunday 
( @Y INT ) 
RETURNS SMALLDATETIME 
AS 
BEGIN 
    DECLARE     @EpactCalc INT,  
        @PaschalDaysCalc INT, 
        @NumOfDaysToSunday INT, 
        @EasterMonth INT, 
        @EasterDay INT 

    SET @EpactCalc = (24 + 19 * (@Y % 19)) % 30 
    SET @PaschalDaysCalc = @EpactCalc - (@EpactCalc / 28) 
    SET @NumOfDaysToSunday = @PaschalDaysCalc - ( 
        (@Y + @Y / 4 + @PaschalDaysCalc - 13) % 7 
    ) 

    SET @EasterMonth = 3 + (@NumOfDaysToSunday + 40) / 44 

    SET @EasterDay = @NumOfDaysToSunday + 28 - ( 
        31 * (@EasterMonth / 4) 
    ) 

    RETURN 
    ( 
        SELECT CONVERT 
        (  SMALLDATETIME, 
                 RTRIM(@Y)  
            + RIGHT('0'+RTRIM(@EasterMonth), 2)  
            + RIGHT('0'+RTRIM(@EasterDay), 2)  
        ) 
    ) 

END 
GO

Good Friday is like this and it uses the Easter function above

CREATE FUNCTION dbo.GetGoodFriday 
( 
    @Y INT 
) 
RETURNS SMALLDATETIME 
AS 
BEGIN 
    RETURN (SELECT dbo.GetEasterSunday(@Y) - 2) 
END 
GO

From here: http://web.archive.org/web/20070611150639/http://sqlserver2000.databases.aspfaq.com/why-should-i-consider-using-an-auxiliary-calendar-table.html

Answer 4

The below code determines Easter through powershell:

function Get-DateOfEaster {
    param(
        [Parameter(ValueFromPipeline)]
        $theYear=(Get-Date).Year
        )

    if($theYear -lt 1583) {
        return $null
    } else {

        # Step 1: Divide the theYear by 19 and store the
        # remainder in variable A.  Example: If the theYear
        # is 2000, then A is initialized to 5.

        $a = $theYear % 19

        # Step 2: Divide the theYear by 100.  Store the integer
        # result in B and the remainder in C.

        $c = $theYear % 100
        $b = ($theYear -$c) / 100

        # Step 3: Divide B (calculated above).  Store the
        # integer result in D and the remainder in E.

        $e = $b % 4
        $d = ($b - $e) / 4

        # Step 4: Divide (b+8)/25 and store the integer
        # portion of the result in F.

        $f = [math]::floor(($b + 8) / 25)

        # Step 5: Divide (b-f+1)/3 and store the integer
        # portion of the result in G.

        $g = [math]::floor(($b - $f + 1) / 3)

        # Step 6: Divide (19a+b-d-g+15)/30 and store the
        # remainder of the result in H.

        $h = (19 * $a + $b - $d - $g + 15) % 30

        # Step 7: Divide C by 4.  Store the integer result
        # in I and the remainder in K.

        $k = $c % 4
        $i = ($c - $k) / 4

        # Step 8: Divide (32+2e+2i-h-k) by 7.  Store the
        # remainder of the result in L.

        $l = (32 + 2 * $e + 2 * $i - $h - $k) % 7

        # Step 9: Divide (a + 11h + 22l) by 451 and
        # store the integer portion of the result in M.

        $m = [math]::floor(($a + 11 * $h + 22 * $l) / 451)

        # Step 10: Divide (h + l - 7m + 114) by 31.  Store
        # the integer portion of the result in N and the
        # remainder in P.

        $p = ($h + $l - 7 * $m + 114) % 31
        $n = (($h + $l - 7 * $m + 114) - $p) / 31

        # At this point p+1 is the day on which Easter falls.
        # n is 3 for March and 4 for April.

        $DateTime = New-Object DateTime $theyear, $n, ($p+1), 0, 0, 0, ([DateTimeKind]::Utc)
        return $DateTime
    }
}

$eastersunday=Get-DateOfEaster 2015
Write-Host $eastersunday

Answer 5

VB .NET Functions for Greek Orthodox and Catholic Easter:

Public Shared Function OrthodoxEaster(ByVal Year As Integer) As Date
    Dim a = Year Mod 19
    Dim b = Year Mod 7
    Dim c = Year Mod 4
    Dim d = (19 * a + 16) Mod 30
    Dim e = (2 * c + 4 * b + 6 * d) Mod 7
    Dim f = (19 * a + 16) Mod 30
    Dim key = f + e + 3
    Dim month = If((key > 30), 5, 4)
    Dim day = If((key > 30), key - 30, key)
    Return New DateTime(Year, month, day)
End Function

Public Shared Function CatholicEaster(ByVal Year As Integer) As DateTime
    Dim month = 3
    Dim a = Year Mod 19 + 1
    Dim b = Year / 100 + 1
    Dim c = (3 * b) / 4 - 12
    Dim d = (8 * b + 5) / 25 - 5
    Dim e = (5 * Year) / 4 - c - 10
    Dim f = (11 * a + 20 + d - c) Mod 30
    If f = 24 Then f += 1
    If (f = 25) AndAlso (a > 11) Then f += 1
    Dim g = 44 - f
    If g < 21 Then g = g + 30
    Dim day = (g + 7) - ((e + g) Mod 7)
    If day > 31 Then
        day = day - 31
        month = 4
    End If
    Return New DateTime(Year, month, day)
End Function

Answer 6

The SQL Server function below is more general than the accepted answer

The accepted answer is only correct for the range (inclusive) : 1900-04-15 to 2099-04-12

It uses the algorithm provided by The United States Naval Observatory (USNO)

http://aa.usno.navy.mil/faq/docs/easter.php

CREATE FUNCTION dbo.GetEasterSunday (@Y INT)
RETURNS DATETIME
AS
    BEGIN 

        -- Source of algorithm : http://aa.usno.navy.mil/faq/docs/easter.php

        DECLARE @c INT = @Y / 100
        DECLARE @n INT = @Y - 19 * (@Y / 19)
        DECLARE @k INT = (@c - 17) / 25
        DECLARE @i INT = @c - @c / 4 - (@c - @k) / 3 + 19 * @n + 15
        SET @i = @i - 30 * (@i / 30)
        SET @i = @i - (@i / 28) * (1 - (@i / 28) * (29 / (@i + 1)) * ((21 - @n) / 11))
        DECLARE @j INT = @Y + @Y / 4 + @i + 2 - @c + @c / 4
        SET @j = @j - 7 * (@j / 7)
        DECLARE @l INT = @i - @j
        DECLARE @m INT = 3 + (@l + 40) / 44
        DECLARE @d INT = @l + 28 - 31 * (@m / 4)

        RETURN 
    ( 
        SELECT CONVERT 
        (  DATETIME, 
                 RTRIM(@Y)  
            + RIGHT('0'+RTRIM(@m), 2)  
            + RIGHT('0'+RTRIM(@d), 2)  
    ) 
    )
    END 


GO