Test if a number is fibonacci

Question

I know how to make the list of the Fibonacci numbers, but i don\'t know how can i test if a given number belongs to the fibonacci list - one way that comes in mind is genera

Answer 1

Since Fibonacci numbers grow exponentially, the method you suggest is pretty fast. Another is this.

Answer 2

#!/bin/bash
victim="144"
curl http://aux.planetmath.org/files/objects/7680/fib.txt | sed 's/^[0-9]*//;s/[ \t]//g' | grep "^$victim$" >/dev/null 2>/dev/null
if [[ $? -eq 0 ]] ; then
    echo "$victim is a fibonacci number"
else
    echo "$victim aint"
fi

Answer 3

A Scala version-

def isFib(n: Int): Boolean = {

def checkFib(f1: Int = 1, f2: Int = 1): Boolean = {

if(n == f1 || n == f2) true
else if(n < f2) false
else checkFib(f2, f1+f2)

}

checkFib()

}

Answer 4

Towards a solution, take a look at Binet's Formula.
(Look for "Closed-Form Expression" under Fibonacci Number on Wikipedia)

It says that the sequence of Fibonacci Number's is created by a simple closed formula:

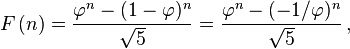
I believe if you solve for n, and test if n is an integer, you'll have your answer.

Edit As @psmears points out, the same Wikipedia article also has a section on detecting Fibonacci numbers. Wikipedia is an excellent source.

Answer 5

See the section "Recognizing Fibonacci numbers" on the wikipedia article about the Fibonacci numbers.

Answer 6

I ran some benchmarks on the methods presented here along with simple addition, pre-computing an array, and memoizing the results in a hash. For Perl, at least, the squaring method is a little bit faster than the logarithmic method, perhaps 20% faster. As abelenky points out, it's a tradeoff between whether you've got the room for squaring bit numbers.

Certainly, the very fastest way is to hash all the Fibonacci numbers in your domain space. Along the lines of another point that abelenky makes, there are only 94 of these suckers that are less than 2^64.

You should just pre-compute them, and put them in a Perl hash, Python dictionary, or whatever.

The properties of Fibonacci numbers are very interesting, but using them to determine whether some integer in a computer program is one is kind of like writing a subroutine to compute pi every time the program starts.