回文串
判断字符串是否是回文串
查找字符串中最长的回文子串
查找字符串中所有的回文子串
执行结果
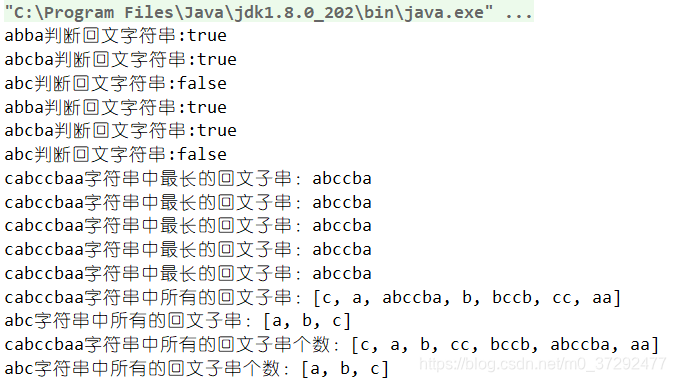
代码
import java.util.ArrayList;
public class StringSeriesOne {
//判断字符串是否是回文串
public boolean isPalindrome(String s){
if(s == null) return false;
char[] array = s.toCharArray();
int left = 0;
int right = array.length -1;
while(left<right){
if(array[left++] != array[right--])
return false;
}
return true;
}
//判断字符串是否是回文串
public boolean isPalindrome1(String s){
if(s==null) return false;
char[] array = s.toCharArray();
for(int i=0; i<array.length/2; i++){
if(array[i] != array[array.length-1-i])
return false;
}
return true;
}
//查找字符串中最长的回文子串:中心拓展法1 O(n2)
public String longestPalindrome1(String s){
//如果回字符串长度小于2直接返回
if(s == null || s.length()<2) return s;
String maxStr = "";
//从第二个字符开始遍历
int j, k, sum;
for(int i=1; i<s.length(); i++){
//结束条件,提高效率
if (s.length()-i <= maxStr.length()/2)
break;
//检验奇数长度的字符串
sum = 1;
for(j=i-1, k=i+1; j>=0 && j<s.length(); j--,k++){
if(s.charAt(j) != s.charAt(k))
break;
sum += 2;
}
if(sum > maxStr.length())
maxStr = s.substring(j+1, k);
//检验偶数长度的字符串
sum =0;
for(j=i-1,k=i; j>=0 && k<s.length(); j--,k++) {
if (s.charAt(j) != s.charAt(k))
break;
sum += 2;
}
if(sum > maxStr.length())
maxStr = s.substring(j+1, k);
}
return maxStr;
}
//查找字符串中最长的回文子串:中心拓展法2 O(n2)
public String longestPalindrome2(String s){
if(s == null || s.length()<2) return s;
int begin = 0, end = 0; //回文子串的始末位置
for(int i=1; i<s.length(); i++){
//奇数子串
int left = i-1;
int right = i+1;
while(left>=0 && right<s.length()-1 && s.charAt(left) == s.charAt(right)){
left--;
right++;
}
if(right-left-2 > end-begin){
begin = left+1;
end = right-1;
}
//偶数子串
left = i-1;
right =i;
while(left>=0 && right<s.length()-1 && s.charAt(left) == s.charAt(right)){
left--;
right++;
}
if(right-left-2 > end-begin){
begin = left+1;
end = right-1;
}
}
return s.substring(begin, end+1);
}
//查找字符串中最长的回文子串:暴力法1 O(n3)
public String longestPalindrome3(String s){
if(s == null || s.length()<2) return s;
int begin = 0, end = 0; //回文子串的始末位置
for(int i=0; i<s.length()-1; i++){
for(int j=i; j<s.length(); j++){
int left = i;
int right = j;
while(left<right && s.charAt(left) == s.charAt(right)){
left++;
right--;
}
if(left>=right && j-i>end-begin){
begin = i;
end = j;
}
}
}
return s.substring(begin, end+1);
}
//查找字符串中最长的回文子串:暴力法2 O(n3)
public String longestPalindrome4(String s){
if(s == null || s.length()<2) return s;
String maxStr = null;
int maxStrLen = 0;
int len = 0;
for(int i=0; i<s.length(); i++){
for(int j=i+1; j<s.length(); j++){
String str = s.substring(i, j);
if(isPalindrome((str)))
len = str.length();
if(len > maxStrLen){
maxStrLen = len;
maxStr = str;
}
len = 0;
}
}
return maxStr;
}
//查找字符串中最长的回文子串:Manacher算法(马拉车算法)O(n)
public String longestPalindrome5(String s){
if(s == null || s.length()<2) return s;
StringBuilder sb = new StringBuilder("$#");
for(int i=0; i<s.length(); i++){
sb.append(String.valueOf(s.charAt(i)));
sb.append("#");
}
sb.append("^");
String str = sb.toString();
//计算p数组
int[] p = new int[str.length()];
int mx=0, id=0;//回文子串的中心位置,回文子串的最后位置
int ansLen=0, ansCenter=0;//回文串长度,中心点位置
for(int i=1; i<str.length()-1; i++){
//mx>i:当前求解位置在已经能够达到的位置之内
p[i] = mx > i ? Math.min( p[2*id-i], mx-i) : 1;
//在已有回文串的基础上求解一个最大回文串
while((i-p[i]>=0) && (i+p[i]<str.length()-1) && (str.charAt(i-p[i])==str.charAt(i+p[i])))
p[i]++;
//判断当前所能到达的最右侧的位置
if(i+p[i]>mx){
mx = i+p[i];//可以到达为止的下一位置
id = i; //对应的中心点
}
//当前求解的最大回文串和存储中的最大回文串,便于之后计算
if(ansLen<p[i]){
ansLen = p[i];
ansCenter = i;
}
}
//在改变后数组的中心位置和半径长度 转化为 原数组中的起始点下标
int begin=(ansCenter-ansLen)/2;
int end=begin+ansLen-1;
//查找结束 将数组转化为字符串返回
return s.substring(begin, end);
}
//查找字符串中所有的回文子串:暴力法O(n3)+O(n)
public ArrayList<String> PalindromicSubstrings1(String s) {
ArrayList<String> list = new ArrayList<String>();
if(s == null || s.length()==0) return list;
for(int i=0; i<s.length(); i++){
for(int j=i+1; j<=s.length(); j++){
String str = s.substring(i, j);
if(isPalindrome((str))){
if(!list.contains(str))
list.add(str);
}
}
}
return list;
}
//查找字符串中所有的回文子串:中心拓展法O(n2)
public ArrayList<String> PalindromicSubstrings2(String s){
ArrayList<String> list = new ArrayList<String>();
if(s == null || s.length() <= 1){
list.add(s);
return list;
}
int count = 0;
for(int i=0; i<s.length(); i++){
getSubList(s, i, i, list);
getSubList(s, i, i+1, list);
}
return list;
}
public void getSubList(String s, int left, int right, ArrayList<String> list){
while(left>=0 && right<s.length() && s.charAt(left)==s.charAt(right)){
if(!list.contains(s.substring(left,right+1)))
list.add(s.substring(left,right+1));
left--;
right++;
}
}
public static void main(String[] args) {
StringSeriesOne s = new StringSeriesOne();
//测试一:判断回文字符串
String str = "abba";
String str1 = "abcba";
String str2 = "abc";
System.out.println(str + "判断回文字符串:" + s.isPalindrome(str));
System.out.println(str1 + "判断回文字符串:" + s.isPalindrome(str1));
System.out.println(str2 + "判断回文字符串:" + s.isPalindrome(str2));
//测试二:判断回文字符串
System.out.println(str + "判断回文字符串:" + s.isPalindrome1(str));
System.out.println(str1 + "判断回文字符串:" + s.isPalindrome1(str1));
System.out.println(str2 + "判断回文字符串:" + s.isPalindrome1(str2));
//测试三:查找字符串中最长的回文子串:中心拓展法1
String str3 = "cabccbaa";
System.out.println(str3 + "字符串中最长的回文子串:" + s.longestPalindrome1(str3));
//测试四:查找字符串中最长的回文子串:中心拓展法2
System.out.println(str3 + "字符串中最长的回文子串:" + s.longestPalindrome2(str3));
//测试五:查找字符串中最长的回文子串:暴力法1
System.out.println(str3 + "字符串中最长的回文子串:" + s.longestPalindrome3(str3));
//测试六:查找字符串中最长的回文子串:暴力法2
System.out.println(str3 + "字符串中最长的回文子串:" + s.longestPalindrome4(str3));
//测试七:查找字符串中最长的回文子串:马拉车算法
System.out.println(str3 + "字符串中最长的回文子串:" + s.longestPalindrome5(str3));
//测试八:查找字符串中所有的回文子串:暴力法
String str4 = "abc";
System.out.println(str3 + "字符串中所有的回文子串:" + s.PalindromicSubstrings1(str3));
System.out.println(str4 + "字符串中所有的回文子串:" + s.PalindromicSubstrings1(str4));
//测试九:查找字符串中所有的回文子串:
System.out.println(str3 + "字符串中所有的回文子串个数:" + s.PalindromicSubstrings2(str3));
System.out.println(str4 + "字符串中所有的回文子串个数:" + s.PalindromicSubstrings2(str4));
}
}
来源:https://blog.csdn.net/m0_37292477/article/details/98871028