机器学习笔记（三）逻辑回归

Classification（分类）

1、问题背景：

特殊的样本点会使得分界点发生漂移，影响准确性。

 

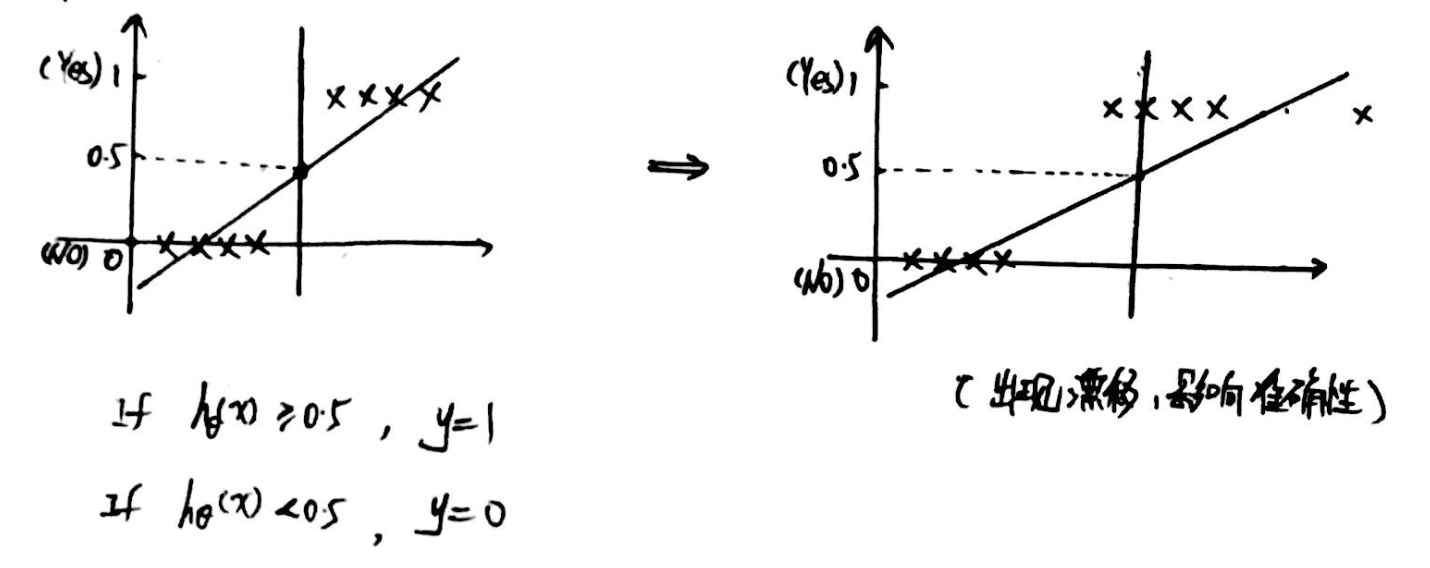
Hypothesis representation（假设函数表达式）

1、Logistic regression Model（逻辑回归模型）：

（1）Sigmoid function / Logistic function S型函数/逻辑函数：

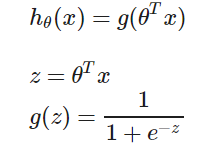
 （2）g(z)图像：

 

（3）h_θ(x) 表示在给定参数θ对于某个特征值x的情况下，y=1的概率：

 

Decision boundary（决策边界）

1、什么是决策边界？

If h_θ(x) = g(θ^Tx) ≥ 0.5，则 y = 1 （即 θ^Tx ≥ 0时）；

If h_θ(x) = g(θ^Tx)＜ 0.5，则 y = 0（即 θ^Tx＜ 0时）.

举例：对于，θ=[-3，1，1]^T，则

y=1，if -3+x₁+x₂ ≥ 0，即分界线为 x₁+x₂ = 3，如下图所示。

 

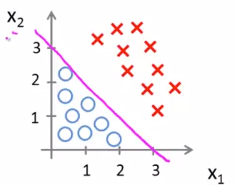
 该边界线称为“决策边界”，边界上方部分y=1，下方部分y=0.

 

2、Non-linear decision boundaries（非线性决策边界）：

例如：

对于θ = [-1，0，0，1，1]^T时，决策边界为x₁² + x₂² = 1，如下图所示。

 

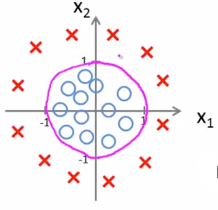
Cost function（代价函数）

 1、数据量化：

训练集：

m个训练样本（每个样本含有n个特征值）：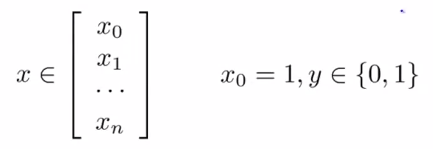

假设函数：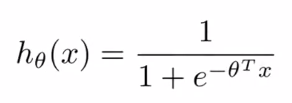

 

2、Logistic regression cost function（逻辑回归代价函数）：

 

   

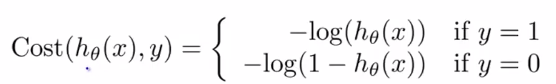
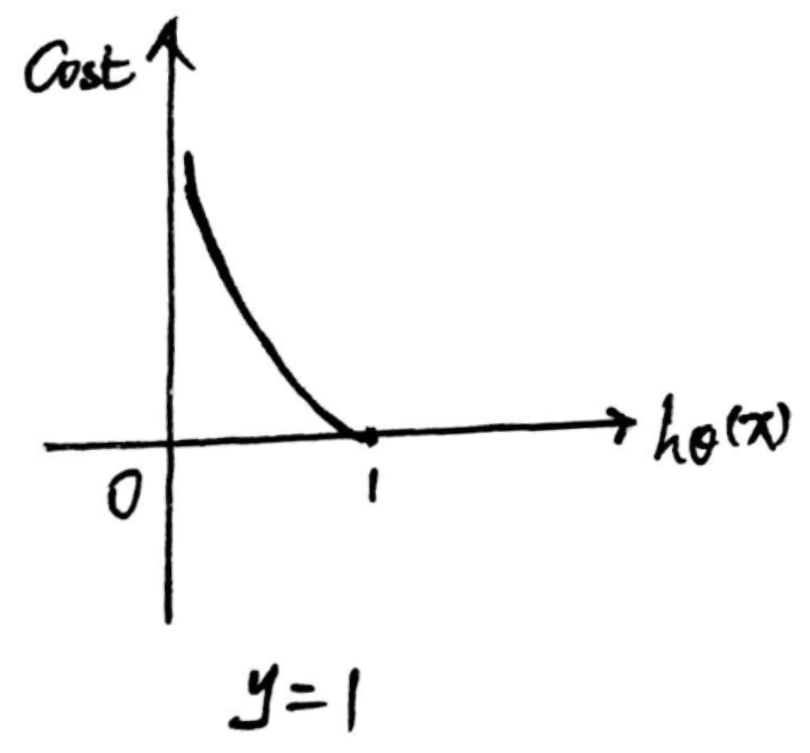
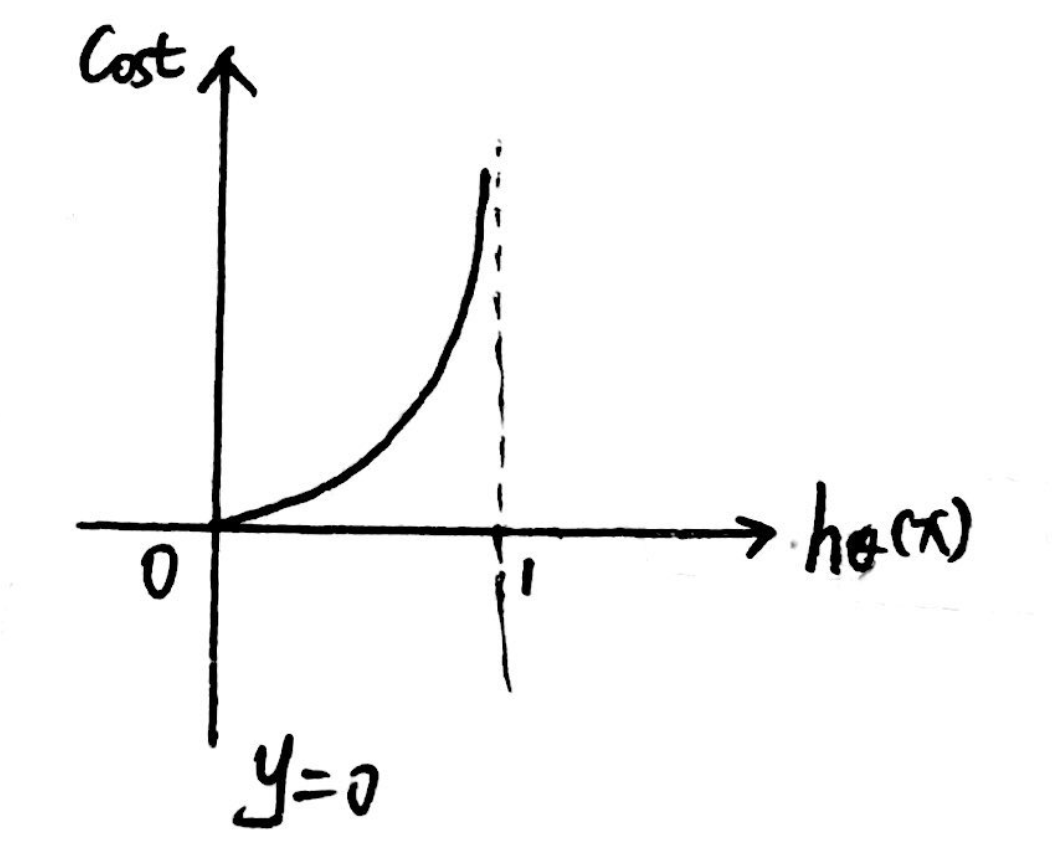
 【理解】

当y = 1时，真实值为1，当预测值越靠近1，则代价越小；

当y = 0时，真实值为0，当预测值越靠近0，则代价越小。

 

3、Simplified cost function（简化代价函数）：

 

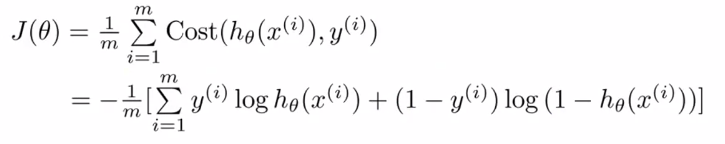
Gradient Descent（梯度下降法）

1、算法流程：

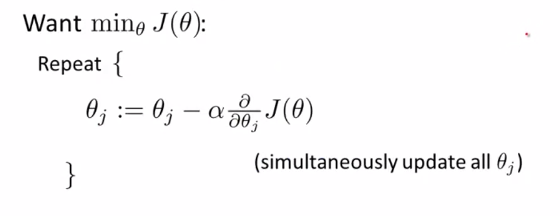
 即：

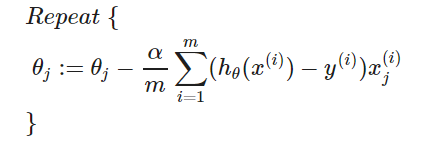
【推导】碰巧跟线性回归的算法一致？

为了推导的方便，对于公式进行了适当简写：

 向量化表示：

 

来源：https://www.cnblogs.com/orangecyh/p/11662022.html