卡特兰数公式推导

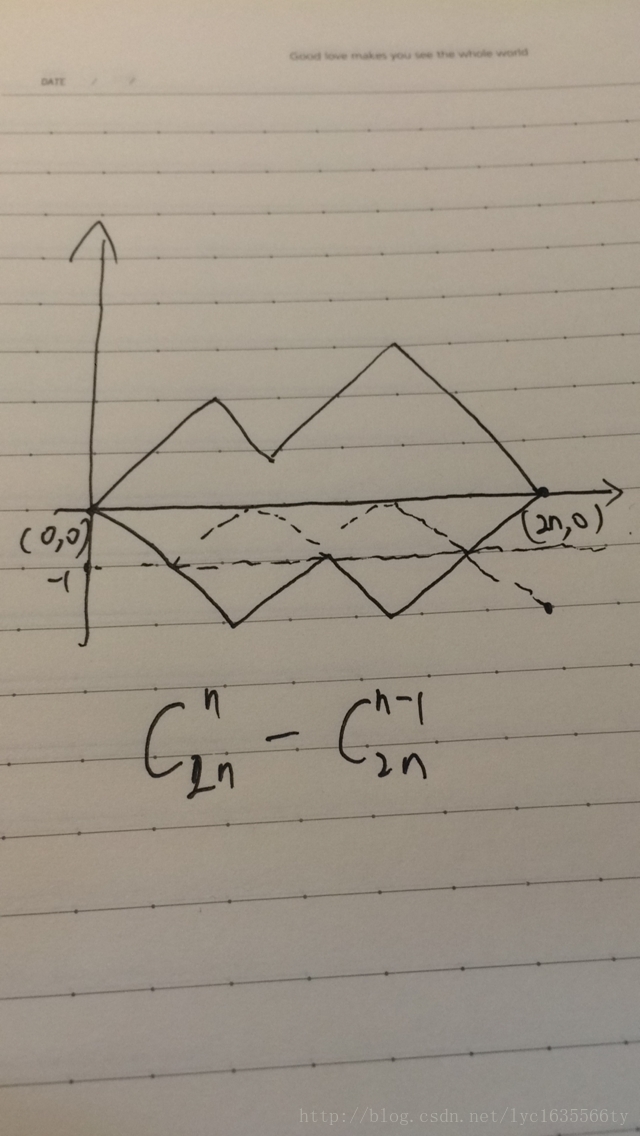
卡特兰数最常见的描述就是2n个球进站出站有多少种顺序

推导：折线法，问题转化为从$<!--//--><![CDATA[// ><!-- <!--//--><![CDATA[// ><!-- (0,0)到(2n,0) //--><!]]]]><![CDATA[> //--><!]]>$ 每次可以向右上或者右下走一波，问在不越过$<!--//--><![CDATA[// ><!-- <!--//--><![CDATA[// ><!-- y=0 //--><!]]]]><![CDATA[> //--><!]]>$ 这条线的情况下，有多少种走法。

所以可以根据总数减去非法数

总数很明显是$<!--//--><![CDATA[// ><!-- <!--//--><![CDATA[// ><!-- c^{n}_{2n} //--><!]]]]><![CDATA[> //--><!]]>$

非法数可以这样算。如果这个过程非法，这条线一定会碰到$<!--//--><![CDATA[// ><!-- <!--//--><![CDATA[// ><!-- y=-1 //--><!]]]]><![CDATA[> //--><!]]>$ 这样我们可以取折线第一次喷到直线$<!--//--><![CDATA[// ><!-- <!--//--><![CDATA[// ><!-- y=-1 //--><!]]]]><![CDATA[> //--><!]]>$的点。然后的折线对$<!--//--><![CDATA[// ><!-- <!--//--><![CDATA[// ><!-- y=-1 //--><!]]]]><![CDATA[> //--><!]]>$做对称，这样所有的点最终都会汇聚到$<!--//--><![CDATA[// ><!-- <!--//--><![CDATA[// ><!-- (2n,-2) //--><!]]]]><![CDATA[> //--><!]]>$这样总数就有$<!--//--><![CDATA[// ><!-- <!--//--><![CDATA[// ><!-- C^{n-1}_{2n} //--><!]]]]><![CDATA[> //--><!]]>$

所以最终结果就是$<!--//--><![CDATA[// ><!-- <!--//--><![CDATA[// ><!-- c^{n}_{2n}-C^{n-1}_{2n} //--><!]]]]><![CDATA[> //--><!]]>$

化简后很容易得到 $$<!--//--><![CDATA[// ><!-- <!--//--><![CDATA[// ><!-- \dfrac{c^{n}_{2n}}{n+1} //--><!]]]]><![CDATA[> //--><!]]>$$

来源：CSDN

作者：lyc1635566ty

链接：https://blog.csdn.net/lyc1635566ty/article/details/73744823