卡特兰数相关及通项公式简单证明

卡特兰数有两个递推公式，两个通项公式（或者说是一个）：
$h_n=\displaystyle\sum_{i=1}^{n-1} h_{i}h_{n-i}$
$h_n=h_{n-1}\frac{4n-2}{n+1}$
$h_n=C_{2n}^{n}-C_{2n}^{n-1}$
$h_n=\frac{C_{2n}^n}{n+1}$
用折线法证明通项公式：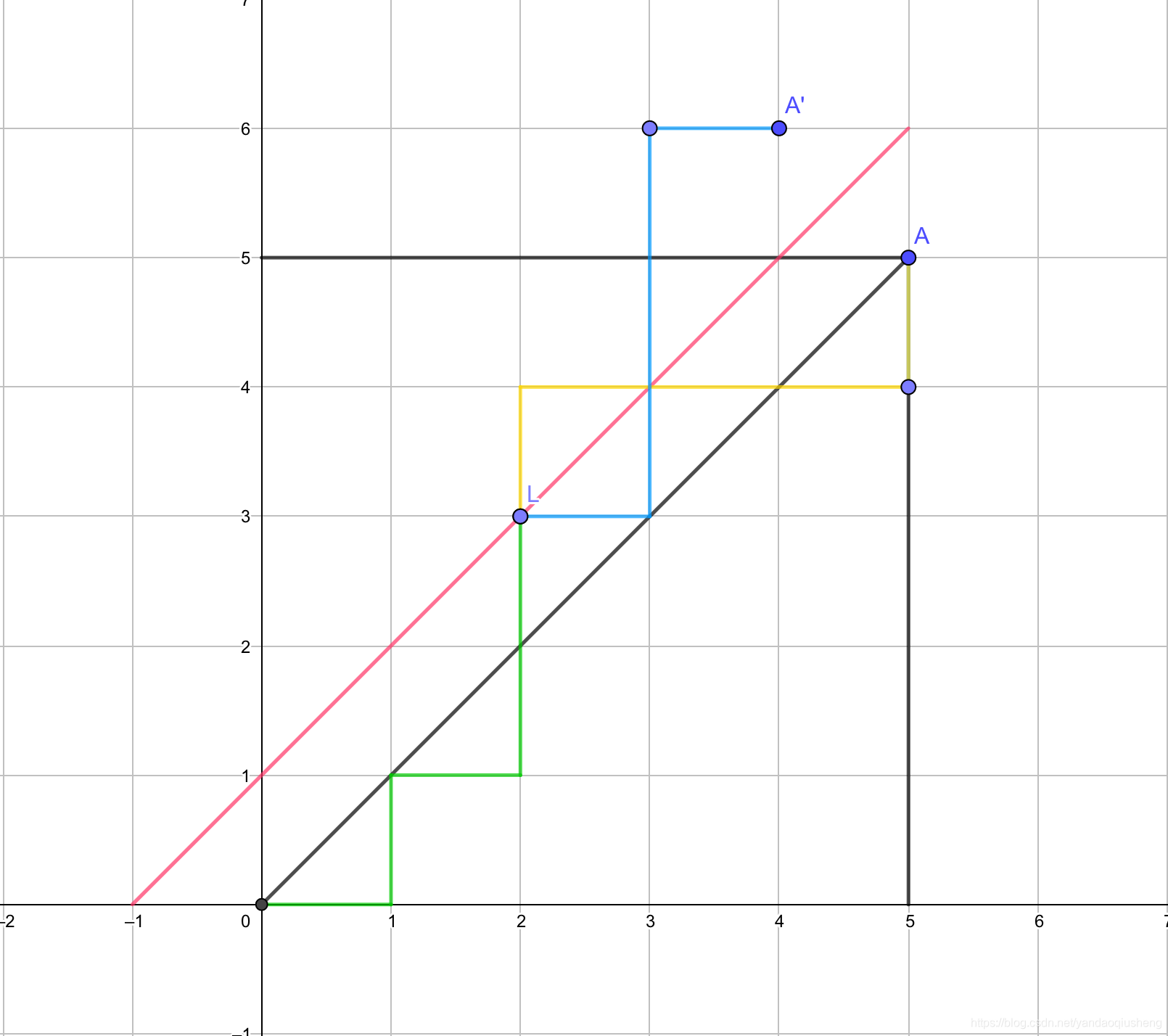

$L$点即为第一次走过$y=x$的点，绿线和黄线组成了一条非法的路径
现在按照$y=x+1$对称，则绿线和蓝线构成了另一条路径
蓝线和黄线总是一一对应的，而蓝线走到的点总是$(n-1,n+1)$
从原点到$A'$的方案数就是$C_{2n}^{n-1}$，得出通项公式

其他

卡特兰数还代表着什么出栈入栈方案数，二叉树构成方案数，在这就不写了，有兴趣可以去别的博客看
卡特兰数的渐进增长：$\frac{4^n}{n^{\frac{3}{2}}\sqrt{\pi}}$
奇数卡特兰数$h_n$满足$n=2^k-1(k=0,1,2...)$（注意$n$是第几项的项数）
前几项：1, 1, 2, 5, 14, 42, 132, 429, 1430, 4862, 16796，注意从第零项开始
图片来源：这里，比我讲的要详细

来源：CSDN

作者：良月澪二

链接：https://blog.csdn.net/yandaoqiusheng/article/details/102653954