归并排序
排序动图演示
整体效果:

排序细节:

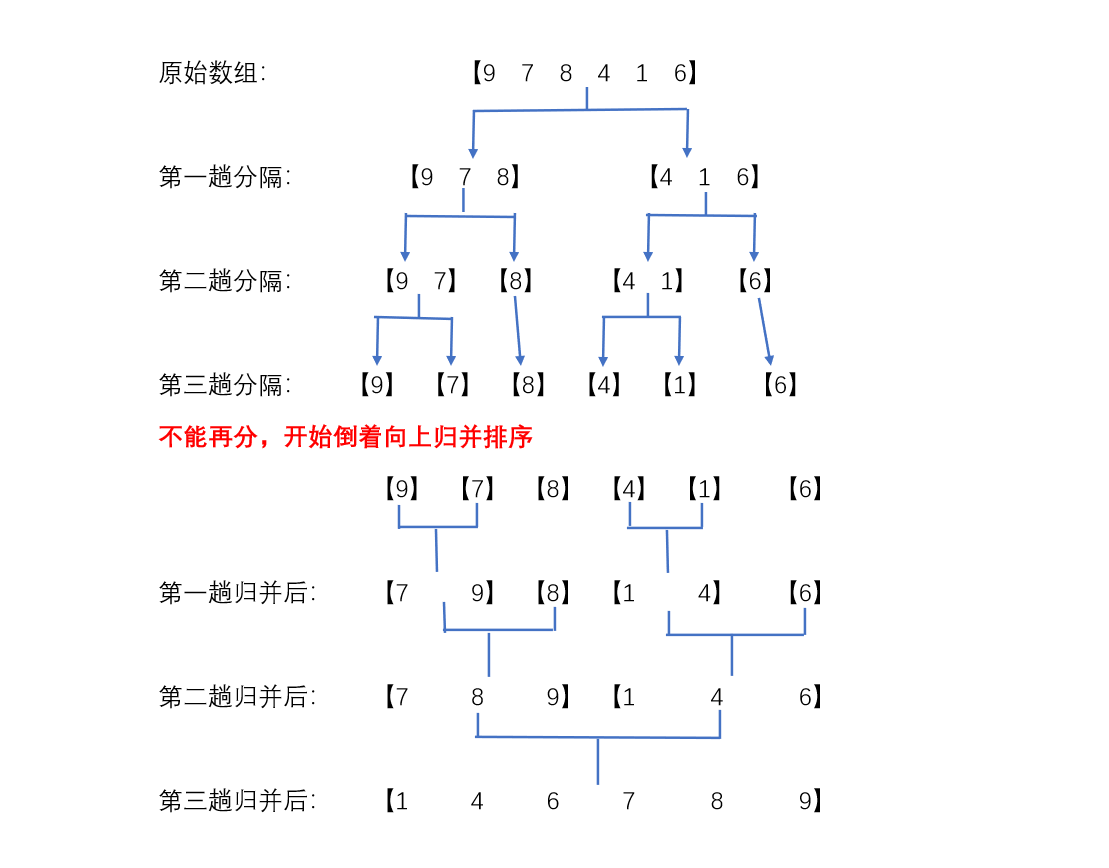
排序原理:
归并排序就是递归得将原始数组递归对半分隔,直到不能再分(只剩下一个元素)后,开始从最小的数组向上归并排序
1. 向上归并排序的时候,需要一个暂存数组用来排序,
2. 将待合并的两个数组,从第一位开始比较,小的放到暂存数组,指针向后移,
3. 直到一个数组空,这时,不用判断哪个数组空了,直接将两个数组剩下的元素追加到暂存数组里,
4. 再将暂存数组排序后的元素放到原数组里,两个数组合成一个,这一趟结束。
我的代码实现:
1 package cn.ftf.mysort;
2
3 import java.util.Arrays;
4
5 public class MyMergeSort {
6 //完善参数,外部调用
7 public static int[] mergeSort(int[] arr) {
8 int [] temp=new int[arr.length];
9 arr=mergeSort1(arr,0,arr.length-1,temp);
10 return arr;
11 }
12 //分+治
13 private static int[] mergeSort1(int[] arr,int left,int right,int[] temp) {
14 if(left<right) {
15 int mid=(left+right)/2;
16 //向左分+治
17 mergeSort1(arr,left,mid,temp);
18 //向右分+治
19 mergeSort1(arr,mid+1,right,temp);
20 merge(arr,left,mid,right,temp);
21 }
22 return arr;
23 }
24 //治
25 private static int[] merge(int[] arr,int left,int mid,int right,int[] temp) {
26 System.out.println("三个边界值:"+left+" "+mid+" "+right);
27 System.out.println();
28 int i=left;
29 int j=mid+1;
30 int t=0; //临时数组的下标
31 while(i<=mid&&j<=right) {
32 if(arr[i]<=arr[j]) {
33 temp[t]=arr[i];
34 i++;
35 t++;
36 }else {
37 temp[t]=arr[j];
38 j++;
39 t++;
40 }
41 }
42 while(i<=mid) {
43 temp[t]=arr[i];
44 i++;
45 t++;
46 }
47 while(j<=right) {
48 temp[t]=arr[j];
49 j++;
50 t++;
51 }
52 //下面将排好序的temp数组copy到arr数组中
53 int arrLeft=left;
54 t=0;
55 while(arrLeft<=right) {
56 arr[arrLeft]=temp[t];
57 t++;
58 arrLeft++;
59 }
60 return arr;
61 }
62 public static void main(String[] args) {
63 int [] arr= {1,7,8,9,12,2,6,10,14,18,1};
64 arr=mergeSort(arr);
65 System.out.println(Arrays.toString(arr));
66 }
67 }
复杂度分析:
1,时间复杂度:无论原始数组是否是有序的,都要递归分隔并向上归并排序,所以时间复杂度始终是O(nlog2n)
2. 空间复杂度:每次两个数组进行归并排序的时候,都会利用一个长度为n的数组作为辅助数组用于保存合并序列,所以空间复杂度为O(n)
基数(桶)排序:
排序算法图解:

排序原理:
基数排序第i趟将待排数组里的每个数的i位数放到tempj(j=1-10)队列中,然后再从这十个队列中取出数据,重新放到原数组里,直到i大于待排数的最大位数。
1.数组里的数最大位数是n位,就需要排n趟,例如数组里最大的数是3位数,则需要排3趟。
2.若数组里共有m个数,则需要十个长度为m的数组tempj(j=0-9)用来暂存i位上数为j的数,例如,第1趟,各位数为0的会被分配到temp0数组里,各位数为1的会被分配到temp1数组里......
3.分配结束后,再依次从tempj数组中取出数据,遵循先进先进原则,例如对数组{1,11,2,44,4},进行第1趟分配后,temp1={1,11},temp2={2},temp4={44,4},依次取出元素后{1,11,2,44,4},第一趟结束
4.循环到n趟后结束,排序完成
我的代码实现:
1 package cn.ftf.mysort;
2 /*
3 * 基数排序(桶排序)
4 */
5 import java.util.Arrays;
6
7 public class MyRadixSort {
8 public static void radixSort(int[] arr) {
9 int bucket[][]=new int[10][arr.length];
10 int maxCount=arr[0];
11 for(int i=1;i<arr.length;i++) {
12 if(maxCount<arr[i]) {
13 maxCount=arr[i];
14 }
15 }
16 //System.out.println("the maxCount is = "+maxCount);
17 int maxLength=(maxCount+"").length();
18 //System.out.println("the maxLength is = "+maxLength);
19 int[] bucketElementCount=new int[10];
20 for(int i=0,n=1;i<maxLength;i++,n*=10) {
21 for(int j=0;j<arr.length;j++) {
22 int compareValue=(arr[j]/n)%10;
23 bucket[compareValue][bucketElementCount[compareValue]]=arr[j];
24 bucketElementCount[compareValue]++;
25 }
26 int arrIndex=0;
27 for(int k=0;k<10;k++) {
28 if(bucketElementCount[k]!=0) {
29 for(int l=0;l<bucketElementCount[k];l++) {
30 arr[arrIndex++]=bucket[k][l];
31 }
32 }
33 bucketElementCount[k]=0;
34 }
35 }
36 }
37 public static void main(String[] args) {
38 int [] arr= {53,3,542,748,14,214};
39 radixSort(arr);
40 System.out.println(Arrays.toString(arr));
41 }
42 }
复杂度分析:
1. 时间复杂度:
每一次关键字的桶分配都需要O(n)的时间复杂度,而且分配之后得到新的关键字序列又需要O(n)的时间复杂度。
假如待排数据可以分为d个关键字,则基数排序的时间复杂度将是O(d*2n) ,当然d要远远小于n,因此基本上还是线性级别的。
系数2可以省略,且无论数组是否有序,都需要从个位排到最大位数,所以时间复杂度始终为O(d*n) 。其中,n是数组长度,d是最大位数。
2. 空间复杂度:
基数排序的空间复杂度为O(n+k),其中k为桶的数量,需要分配n个数。
归并排序和基数排序速度测试:
1 import cn.ftf.mysort.MyBubbleSort;
2 import cn.ftf.mysort.MyChooseSort;
3 import cn.ftf.mysort.MyInserSort;
4 import cn.ftf.mysort.MyMergeSort;
5 import cn.ftf.mysort.MyQuickSort;
6 import cn.ftf.mysort.MyRadixSort;
7 import cn.ftf.mysort.MyShellSort;
8 /*
9 * 我的排序算法速度测试
10 */
11 public class MySortText {
12 public static void main(String[] args) {
13 int[] arr;
14 arr=new int[8000000];
15 for(int i =0; i < 8000000;i++) {
16 arr[i] = (int)(Math.random() * 10000);
17 }
18 firstTime=System.currentTimeMillis();
19 MyMergeSort.mergeSort(arr);
20 secondTime=System.currentTimeMillis();
21 System.out.println("归并排序用时:"+(secondTime-firstTime));
22
23 arr=new int[8000000];
24 for(int i =0; i < 8000000;i++) {
25 arr[i] = (int)(Math.random() * 10000);
26 }
27 firstTime=System.currentTimeMillis();
28 MyRadixSort.radixSort(arr);
29 secondTime=System.currentTimeMillis();
30 System.out.println("基数排序用时:"+(secondTime-firstTime));
31 }
32
33 }
测试结果:

归并排序和基数排序的使用:
大体量数据在排序时用快速排序较多,归并排序和基数排序都是稳定的排序算法。基数排序比之前排序算法都要快很多,不过是在建立在额外占用大量内存的代价上实现的。