排序算法
排序也称排序算法(Sort Algorithm),排序是将一组数据,依指定的顺序进行排列的过程。
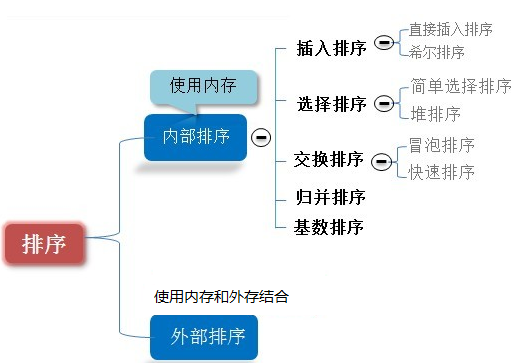
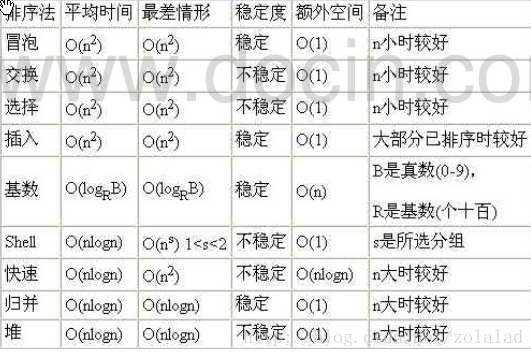
排序的分类:
1) 内部排序:指将需要处理的所有数据都加载到内部存储器中进行排序。
2) 外部排序法:数据量过大,无法全部加载到内存中,需要借助外部存储进行排序。
3) 常见的排序算法分类(见右图):
l算法的时间复杂度
度量一个程序(算法)执行时间的两种方法
这种方法可 行 , 但 是有两个 问题 :
通过分析某个算法的 时间复杂度 来判断哪个算法更优 .
时间频度
时间频度:一个算法花费的时间与算法中语句的执行次数成正比例,哪个算法中语句执行次数多,它花费时间就多。一个算法中的语句执行次数称为语句频度或时间频度。记为T(n)。
举例说明-基本案例
比如计算1-100所有数字之和, 我们设计两种算法:
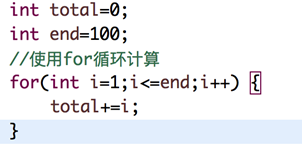
T(n)=n+1;

T(n)=1;
举例说明-忽略常数项
|
|
T(n)=2n+20 |
T(n)=2*n |
T(3n+10) |
T(3n) |
| 1 |
22 |
2 |
13 |
3 |
| 2 |
24 |
4 |
16 |
6 |
| 5 |
30 |
10 |
25 |
15 |
| 8 |
36 |
16 |
34 |
24 |
| 15 |
50 |
30 |
55 |
45 |
| 30 |
80 |
60 |
100 |
90 |
| 100 |
220 |
200 |
310 |
300 |
| 300 |
620 |
600 |
910 |
900 |
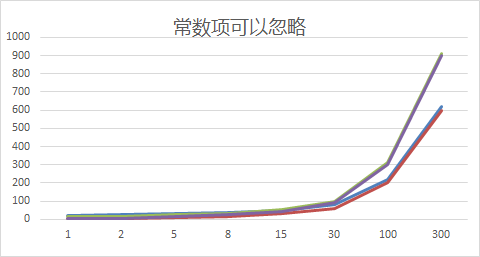
结论:
忽略低次项
|
|
T(n)=2n^2+3n+10 |
T(2n^2) |
T(n^2+5n+20) |
T(n^2) |
| 1 |
15 |
2 |
26 |
1 |
| 2 |
24 |
8 |
34 |
4 |
| 5 |
75 |
50 |
70 |
25 |
| 8 |
162 |
128 |
124 |
64 |
| 15 |
505 |
450 |
320 |
225 |
| 30 |
1900 |
1800 |
1070 |
900 |
| 100 |
20310 |
20000 |
10520 |
10000 |
结论: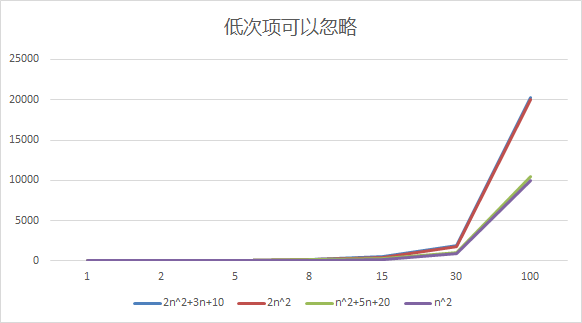
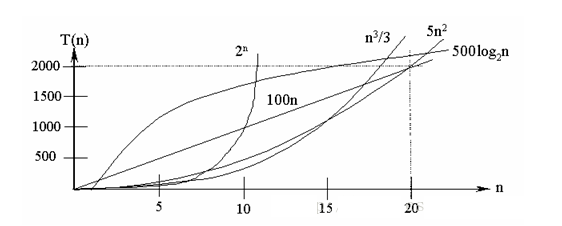
时间复杂度
常见的时间复杂度
1)常数阶O(1)
无论代码执行了多少行,只要是没有循环等复杂结构,那这个代码的时间复杂度就都是O(1)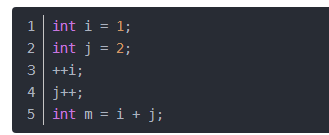
上述代码在执行的时候,它消耗的时候并不随着某个变量的增长而增长,那么无论这类代码有多长,即使有几万几十万行,都可以用O(1)来表示它的时间复杂度。
2)对数阶O(log2n)
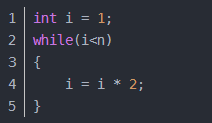
在while循环里面,每次都将 i 乘以 2,乘完之后,i 距离 n 就越来越近了。假设循环x次之后,i 就大于 2 了,此时这个循环就退出了,也就是说 2 的 x 次方等于 n,那么 x = log2n也就是说当循环 log2n 次以后,这个代码就结束了。因此这个代码的时间复杂度为:O(log2n) 。 O(log2n) 的这个2 时间上是根据代码变化的,i = i * 3 ,则是 O(log3n) .

3)线性阶O(n)
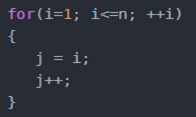
说明:这段代码,for循环里面的代码会执行n遍,因此它消耗的时间是随着n的变化而变化的,因此这类代码都可以用O(n)来表示它的时间复杂度
4)线性对数阶O(nlogN)
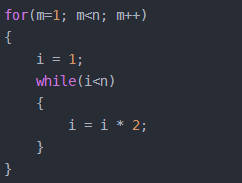
说明:线性对数阶O(nlogN) 其实非常容易理解,将时间复杂度为O(logn)的代码循环N遍的话,那么它的时间复杂度就是 n * O(logN),也就是了O(nlogN)
5)平方阶O(n²)
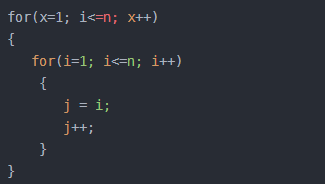
说明:平方阶O(n²) 就更容易理解了,如果把 O(n) 的代码再嵌套循环一遍,它的时间复杂度就是 O(n²),这段代码其实就是嵌套了2层n循环,它的时间复杂度就是 O(n*n),即 O(n²) 如果将其中一层循环的n改成m,那它的时间复杂度就变成了 O(m*n)
6)立方阶O(n³)、K次方阶O(n^k)
参考上面的O(n²) 去理解就好了,O(n³)相当于三层n循环,其它的类似
算法的时间复杂度
平均时间复杂度和最坏时间复杂度
算法的空间复杂度简介
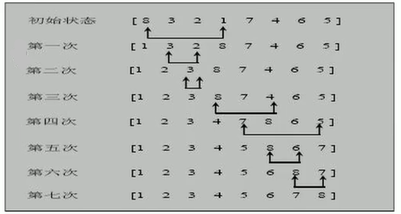
冒泡排序
冒泡排序(Bubble Sorting)的基本思想是:通过对待排序序列从前向后(从下标较小的元素开始),依次比较相邻元素的值,若发现逆序则交换,使值较大的元素逐渐从前移向后部,就象水底下的气泡一样逐渐向上冒。

/**
* @author Sun.Mr
* @create 2019-09-20 22:19
*/
public class Bubblesort {
public static void main(String[] args) {
int arr[] ={3,-2,9,10,7};
int temp = 0;//临时变量
for (int i = 0; i <arr.length ; i++) {
//如果前面的数比后面的数大,则交换
for (int j = 0; j <arr.length-1-i ; j++) {
if (arr[j] > arr[j+1]) {
temp=arr[j];
arr[j] =arr[j+1];
arr[j+1]=temp;
}
}
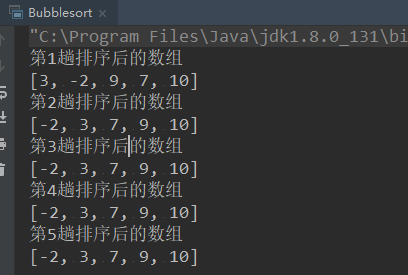
System.out.println("第"+(i+1)+"趟排序后的数组");
System.out.println(Arrays.toString(arr));
}
}
}
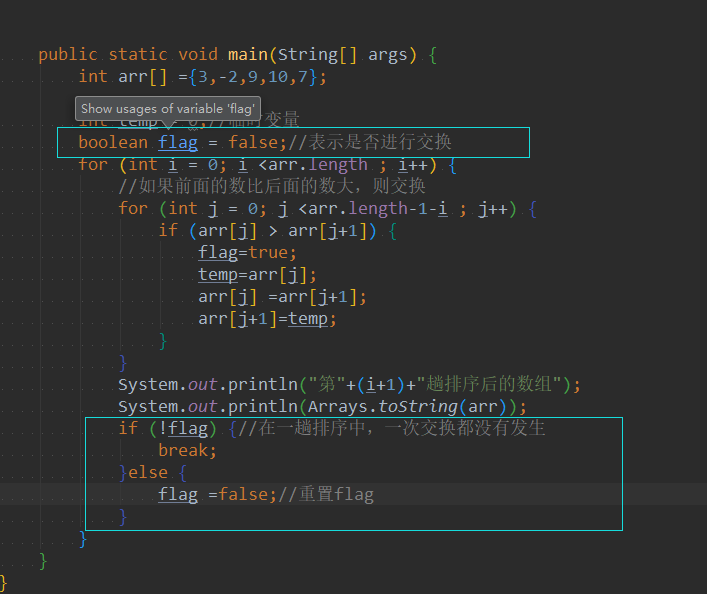
优化:因为排序的过程中,各元素不断接近自己的位置,如果一趟比较下来没有进行过交换,就说明序列有序,因此要在排序过程中设置一个标志flag判断元素是否进行过交换。从而减少不必要的比较。
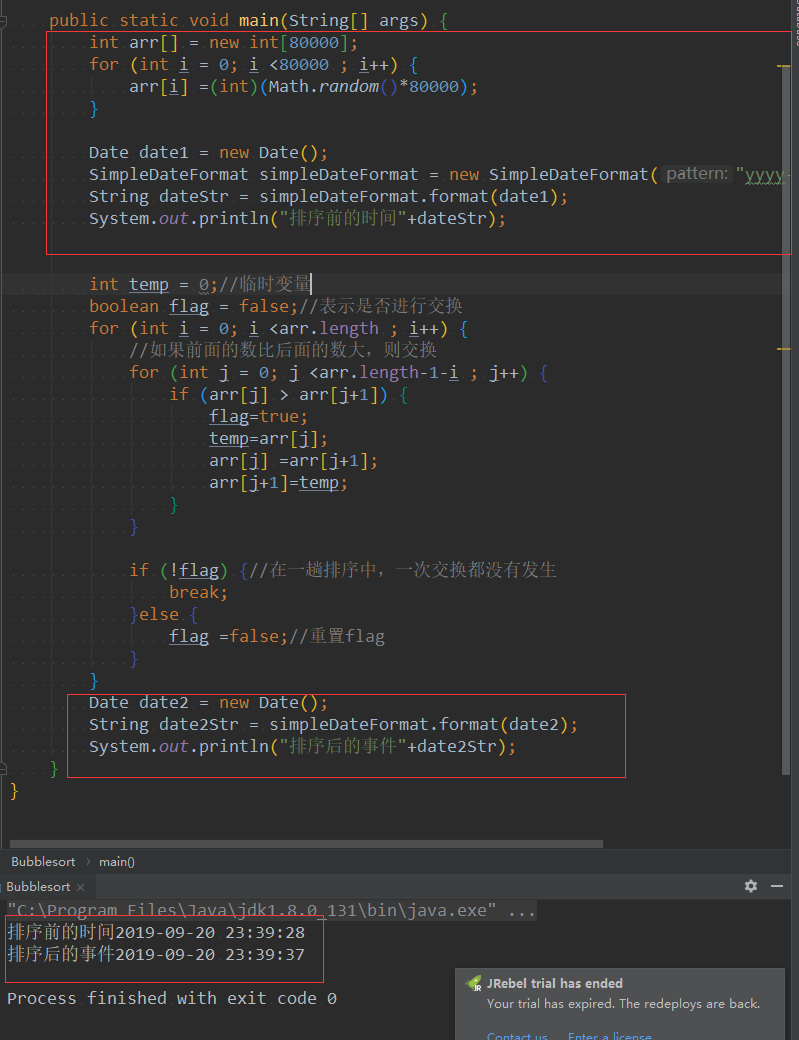
测试8000个数的冒泡排序的时间
选择排序
选择式排序也属于内部排序法,是从欲排序的数据中,按指定的规则选出某一元素,再依规定交换位置后达到排序的目的。
选择排序思想:
选择排序(select sorting)也是一种简单的排序方法。它的基本思想是:第一次从arr[0]~arr[n-1]中选取最小值,与arr[0]交换,第二次从arr[1]~arr[n-1]中选取最小值,与arr[1]交换,第三次从arr[2]~arr[n-1]中选取最小值,与arr[2]交换,…,第i次从arr[i-1]~arr[n-1]中选取最小值,与arr[i-1]交换,…, 第n-1次从arr[n-2]~arr[n-1]中选取最小值,与arr[n-2]交换,总共通过n-1次,得到一个按排序码从小到大排列的有序序列。
选择排序的思路图解