先讲经典快排。
数组最后一个值是 X (划分值)
争取<= X 的值放在左边,>= X 的放在右边。
开始一个数组,最后一个值作为划分值。
然后整个数组分为两个部分,<=X 的在左边,>=X 的在右边。
然后<=X 的当做一个全新的数组,再次把最后一个值当做划分值。两个部分拆分下去,让整个部分都有序。以上是经典快排。
改进:
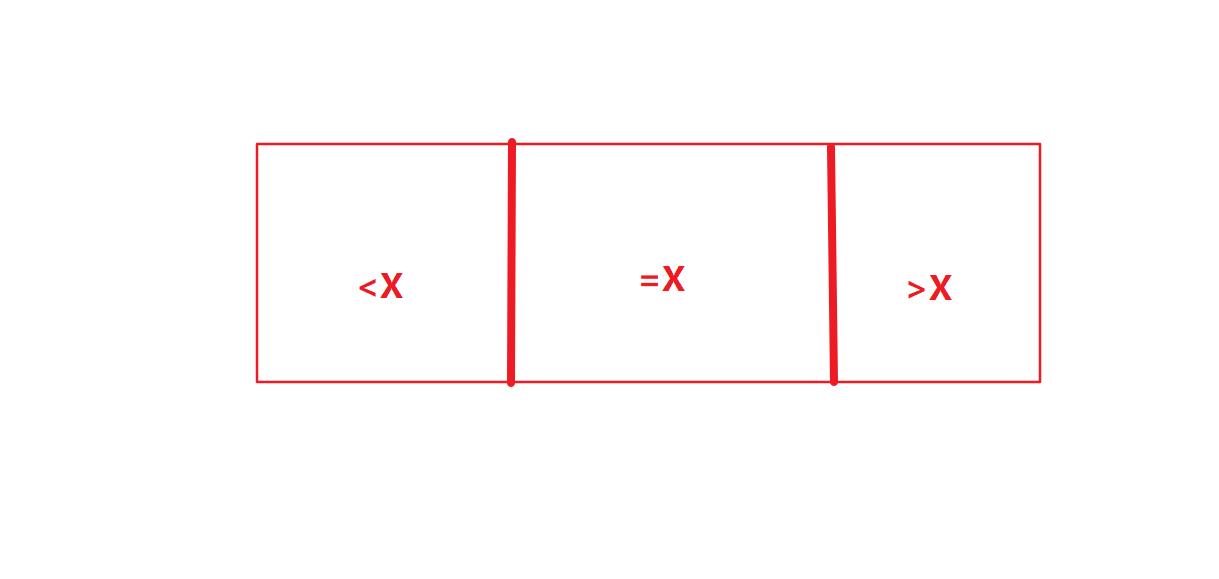
=x 的部分不动,小于X 的区域和大于 X 的区域继续这样的过程——递归。
package suanfa;
public class quickSort {
public static void quicksort(int[] arr) { //重载
if (arr == null || arr.length < 2) {
return;
}
quicksort(arr, 0, arr.length - 1);
}
public static void quicksort(int[] arr, int L, int R) {
if (L < R) { // 临界条件
//swap(arr,L+(int)(Math.random()*(R-L+1)),R); 这时一个随机快排
int[] p = partition(arr, L, R); //经过一个p过程,返回一个数组,是等于区域的左右两个边界
quicksort(arr, L, p[0] - 1); // 左边部分继续递归
quicksort(arr, p[1] + 1, R); // 右边部分继续递归
}
}
public static int[] partition(int[] arr, int L, int R) {
int less = L - 1; // less 是小于区域的
int more = R; // more是 大于区域的
while (L < more) { //循环条件,只要左边界<右边界,循环下去
if (arr[L] < arr[R]) {
swap(arr, ++less, L++);
} else if (arr[L] > arr[R]) {
swap(arr, --more, L);
} else {
L++;
}
}
swap(arr, more, R); //边界代码一开始没有参与,最后要归位
return new int[] { less + 1, more }; //返回一个数组
}
public static void swap(int[] arr, int i, int j) {
int tmp = arr[i];
arr[i] = arr[j];
arr[j] = tmp;
}
public static void main(String[] args) {
int[] arr = { 0, 1, -94, 65, 888 };
System.out.println(java.util.Arrays.toString(arr));
quicksort(arr);
System.out.println(java.util.Arrays.toString(arr));
}
}