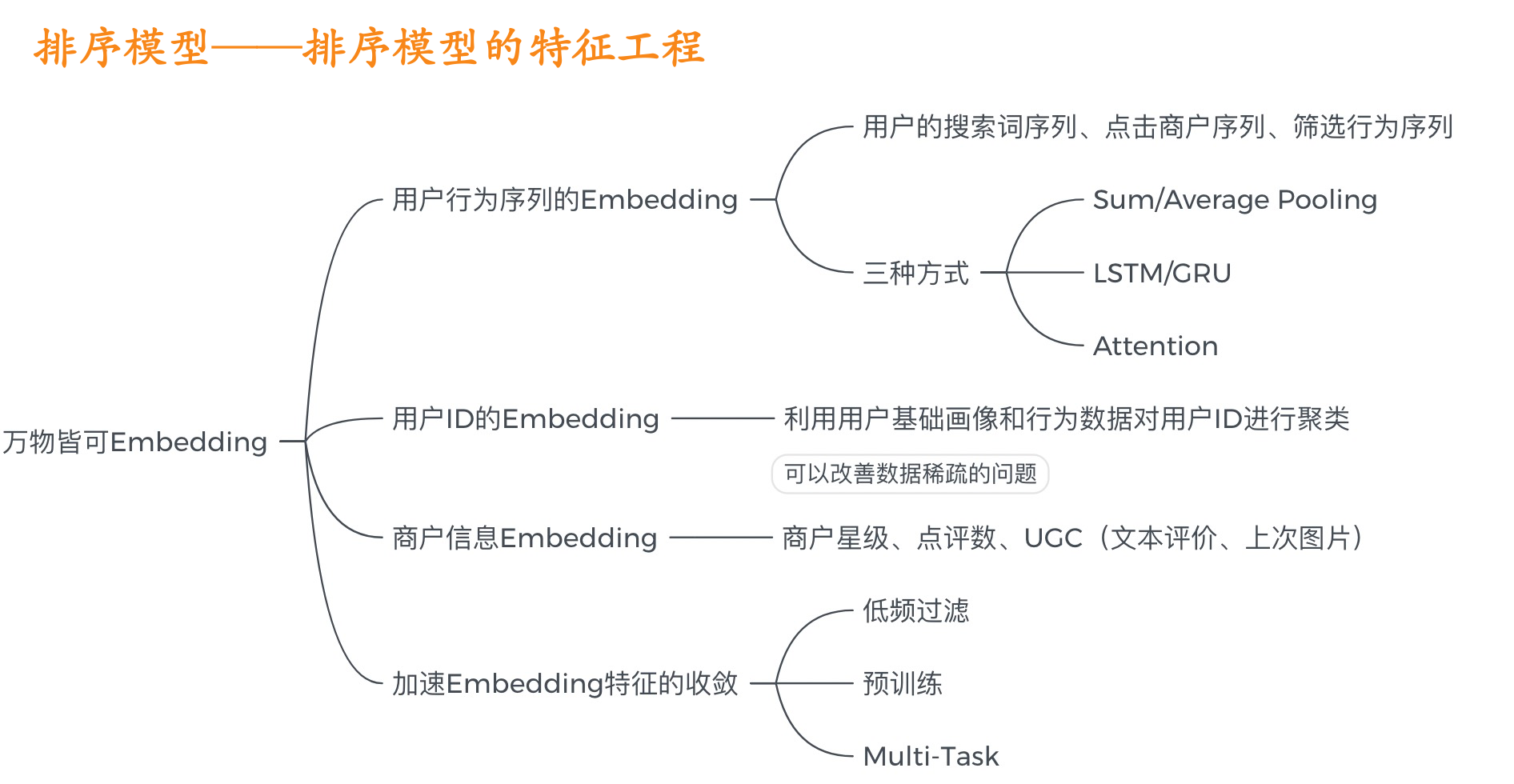
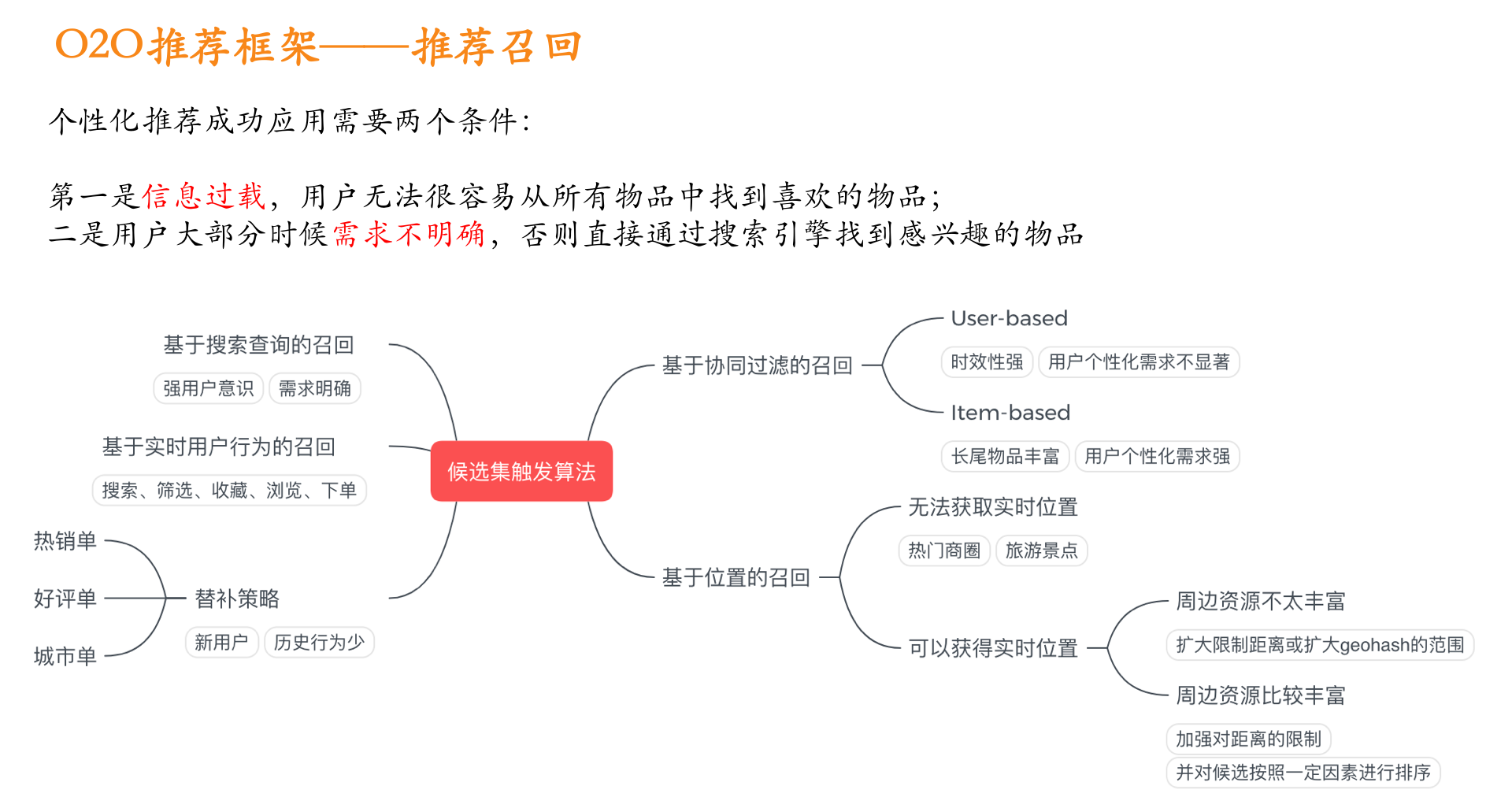
1、原理

Deep&Cross Network模型我们下面将简称DCN模型：

一个DCN模型从嵌入和堆积层开始，接着是一个交叉网络和一个与之平行的深度网络，之后是最后的组合层，它结合了两个网络的输出。完整的网络模型如图：

嵌入和堆叠层
我们考虑具有离散和连续特征的输入数据。在网络规模推荐系统中，如CTR预测，输入主要是分类特征，如“country=usa”。这些特征通常是编码为独热向量如“[ 0,1,0 ]”；然而，这往往导致过度的高维特征空间大的词汇。

为了减少维数，我们采用嵌入过程将这些离散特征转换成实数值的稠密向量（通常称为嵌入向量）：

然后，我们将嵌入向量与连续特征向量叠加起来形成一个向量：

拼接起来的向量X0将作为我们Cross Network和Deep Network的输入

Cross Network
交叉网络的核心思想是以有效的方式应用显式特征交叉。交叉网络由交叉层组成，每个层具有以下公式：

一个交叉层的可视化如图所示:

可以看到，交叉网络的特殊结构使交叉特征的程度随着层深度的增加而增大。多项式的最高程度（就输入X0而言）为L层交叉网络L + 1。如果用Lc表示交叉层数，d表示输入维度。然后，参数的数量参与跨网络参数为：d * Lc * 2 (w和b)

交叉网络的少数参数限制了模型容量。为了捕捉高度非线性的相互作用，模型并行地引入了一个深度网络。

Deep Network

深度网络就是一个全连接的前馈神经网络，每个深度层具有如下公式：

Combination Layer

链接层将两个并行网络的输出连接起来，经过一层全链接层得到输出：

如果采用的是对数损失函数，那么损失函数形式如下：

总结
DCN能够有效地捕获有限度的有效特征的相互作用，学会高度非线性的相互作用，不需要人工特征工程或遍历搜索，并具有较低的计算成本。
论文的主要贡献包括：

1）提出了一种新的交叉网络，在每个层上明确地应用特征交叉，有效地学习有界度的预测交叉特征，并且不需要手工特征工程或穷举搜索。
2）跨网络简单而有效。通过设计，各层的多项式级数最高，并由层深度决定。网络由所有的交叉项组成，它们的系数各不相同。
3）跨网络内存高效，易于实现。
4）实验结果表明，交叉网络（DCN）在LogLoss上与DNN相比少了近一个量级的参数量。

这个是从论文中翻译过来的，哈哈。

2、实现解析

本文的代码根据之前DeepFM的代码进行改进，我们只介绍模型的实现部分，其他数据处理的细节大家可以参考我的github上的代码：
https://github.com/princewen/tensorflow_practice/tree/master/Basic-DCN-Demo

数据下载地址：https://www.kaggle.com/c/porto-seguro-safe-driver-prediction

不去下载也没关系，我在github上保留了几千行的数据用作模型测试。

模型输入

模型的输入主要有下面几个部分：

self.feat_index = tf.placeholder(tf.int32,                                 shape=[None,None],                                 name='feat_index')self.feat_value = tf.placeholder(tf.float32,                               shape=[None,None],                               name='feat_value')self.numeric_value = tf.placeholder(tf.float32,[None,None],name='num_value')self.label = tf.placeholder(tf.float32,shape=[None,1],name='label')self.dropout_keep_deep = tf.placeholder(tf.float32,shape=[None],name='dropout_deep_deep')

可以看到，这里与DeepFM相比，一个明显的变化是将离散特征和连续特征分开，连续特征不在转换成embedding进行输入，所以我们的输入共有五部分。
feat_index是离散特征的一个序号，主要用于通过embedding_lookup选择我们的embedding。feat_value是对应离散特征的特征值。numeric_value是我们的连续特征值。label是实际值。还定义了两个dropout来防止过拟合。

权重构建

权重主要包含四部分，embedding层的权重，cross network中的权重，deep network中的权重以及最后链接层的权重，我们使用一个字典来表示：

def _initialize_weights(self):weights = dict()#embeddingsweights['feature_embeddings'] = tf.Variable(    tf.random_normal([self.cate_feature_size,self.embedding_size],0.0,0.01),    name='feature_embeddings')weights['feature_bias'] = tf.Variable(tf.random_normal([self.cate_feature_size,1],0.0,1.0),name='feature_bias')#deep layersnum_layer = len(self.deep_layers)glorot = np.sqrt(2.0/(self.total_size + self.deep_layers[0]))weights['deep_layer_0'] = tf.Variable(    np.random.normal(loc=0,scale=glorot,size=(self.total_size,self.deep_layers[0])),dtype=np.float32)weights['deep_bias_0'] = tf.Variable(    np.random.normal(loc=0,scale=glorot,size=(1,self.deep_layers[0])),dtype=np.float32)for i in range(1,num_layer):    glorot = np.sqrt(2.0 / (self.deep_layers[i - 1] + self.deep_layers[i]))    weights["deep_layer_%d" % i] = tf.Variable(        np.random.normal(loc=0, scale=glorot, size=(self.deep_layers[i - 1], self.deep_layers[i])),        dtype=np.float32)  # layers[i-1] * layers[i]    weights["deep_bias_%d" % i] = tf.Variable(        np.random.normal(loc=0, scale=glorot, size=(1, self.deep_layers[i])),        dtype=np.float32)  # 1 * layer[i]for i in range(self.cross_layer_num):    weights["cross_layer_%d" % i] = tf.Variable(        np.random.normal(loc=0, scale=glorot, size=(self.total_size,1)),        dtype=np.float32)    weights["cross_bias_%d" % i] = tf.Variable(        np.random.normal(loc=0, scale=glorot, size=(self.total_size,1)),        dtype=np.float32)  # 1 * layer[i]# final concat projection layerinput_size = self.total_size + self.deep_layers[-1]glorot = np.sqrt(2.0/(input_size + 1))weights['concat_projection'] = tf.Variable(np.random.normal(loc=0,scale=glorot,size=(input_size,1)),dtype=np.float32)weights['concat_bias'] = tf.Variable(tf.constant(0.01),dtype=np.float32)return weights

计算网络输入
这一块我们要计算两个并行网络的输入X0，我们需要将离散特征转换成embedding，同时拼接上连续特征：

# modelself.embeddings = tf.nn.embedding_lookup(self.weights['feature_embeddings'],self.feat_index) # N * F * Kfeat_value = tf.reshape(self.feat_value,shape=[-1,self.field_size,1])self.embeddings = tf.multiply(self.embeddings,feat_value)self.x0 = tf.concat([self.numeric_value,                     tf.reshape(self.embeddings,shape=[-1,self.field_size * self.embedding_size])]                    ,axis=1)

Cross Network
根据论文中的计算公式，一步步计算得到cross network的输出：

# cross_partself._x0 = tf.reshape(self.x0, (-1, self.total_size, 1))x_l = self._x0for l in range(self.cross_layer_num):    x_l = tf.tensordot(tf.matmul(self._x0, x_l, transpose_b=True),                        self.weights["cross_layer_%d" % l],1) + self.weights["cross_bias_%d" % l] + x_lself.cross_network_out = tf.reshape(x_l, (-1, self.total_size))

Deep Network
这一块就是一个多层全链接神经网络：

self.y_deep = tf.nn.dropout(self.x0,self.dropout_keep_deep[0])for i in range(0,len(self.deep_layers)):    self.y_deep = tf.add(tf.matmul(self.y_deep,self.weights["deep_layer_%d" %i]), self.weights["deep_bias_%d"%i])    self.y_deep = self.deep_layers_activation(self.y_deep)    self.y_deep = tf.nn.dropout(self.y_deep,self.dropout_keep_deep[i+1])

Combination Layer
最后将两个网络的输出拼接起来，经过一层全链接得到最终的输出：

# concat_partconcat_input = tf.concat([self.cross_network_out, self.y_deep], axis=1)self.out = tf.add(tf.matmul(concat_input,self.weights['concat_projection']),self.weights['concat_bias'])

定义损失
这里我们可以选择logloss或者mse，并加上L2正则项：

# lossif self.loss_type == "logloss":    self.out = tf.nn.sigmoid(self.out)    self.loss = tf.losses.log_loss(self.label, self.out)elif self.loss_type == "mse":    self.loss = tf.nn.l2_loss(tf.subtract(self.label, self.out))# l2 regularization on weightsif self.l2_reg > 0:    self.loss += tf.contrib.layers.l2_regularizer(        self.l2_reg)(self.weights["concat_projection"])    for i in range(len(self.deep_layers)):        self.loss += tf.contrib.layers.l2_regularizer(            self.l2_reg)(self.weights["deep_layer_%d" % i])    for i in range(self.cross_layer_num):        self.loss += tf.contrib.layers.l2_regularizer(            self.l2_reg)(self.weights["cross_layer_%d" % i])

剩下的代码就不介绍啦！

好啦，本文只是提供一个引子，有关DCN的知识大家可以更多的进行学习呦。