[Java] 计蒜客---苹果数 (dfs序)

一、内容

二、思路

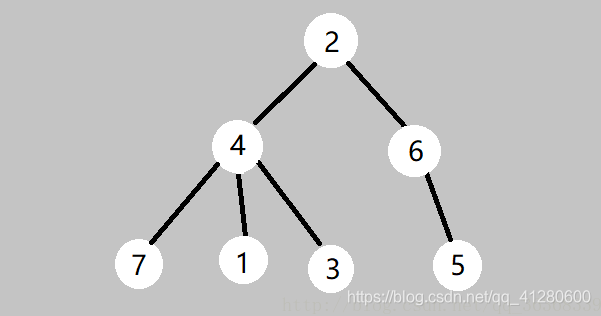
• 用dfs序将树形结构转换为线性结构，然后用线段树或树状数据进行维护。

• 当用dfs遍历这棵树的时候，进入到这个点是有一个进入时间in，递归完成后有一个退出时间out,所以这个点和它子树所在的区间就是【in[u], out[u]】(u就是这个点)。
  

  	static int[] in = new int[N + 5]; // in[j] 代表节点j子树的左端点，也就是节点所在端点
  	static int[] ot = new int[N + 5];// ot[j] 代表节点子树以哪个右断点
  	static int time;
  
  	// 建立dfs序
  	static void dfs(int u) {
  		in[u] = ++time; //进入的时间
  		for (int j = head[u]; j != -1; j = e[j].next) {
  			int v = e[j].v;
  			dfs(v);
  		}
  		// 出去的时间 递归结束
  		ot[u] = time;
  	}
  

• 获得了以u为根节点的区间，就转化成了求这个区间里面有多少个苹果。

• 更新： 用一个vis数组记录这个点上是否有苹果，若有苹果就以当前节点所在区间进行-1，若没有苹果进行+1。

三、代码

import java.io.*;
import java.math.*;
import java.util.*;

public class I_苹果树 {
	static int N = 1000000;
	static boolean[] vis = new boolean[N + 5];
	static E[] e = new E[N + 5];
	static int len, n, m;
	static int[] head = new int[N + 5];
	static int[] c = new int[N + 5];
	static PrintWriter out = new PrintWriter(System.out);
	static Reader cin = new Reader();

	static void add(int u, int v) {
		e[len] = new E(v, head[u]);
		head[u] = len++;
	}

	public static void main(String[] args) {
		Arrays.fill(head, -1);
		n = cin.nextInt();
		m = cin.nextInt();
		int u, v;
		for (int i = 1; i < n; i++) {
			u = cin.nextInt();
			v = cin.nextInt();
			add(u, v);
		}
		dfs(1);
		// 建立区间数
		for (int i = 1; i <= n; i++) {
			update(i, 1); // 每个区间都有一个苹果
		}
		String x;
		int y;
		for (int i = 1; i <= m; i++) {
			x = cin.next();
			y = cin.nextInt();
			if (x.equals("C")) {
				if (vis[y]) {
					// 表示没有苹果
					update(in[y], 1);
					vis[y] = false;
				} else {
					// 有苹果 摘掉
					vis[y] = true;
					update(in[y], -1);
				}
			} else {
				// 查询 [in[y], ot[y]] 区间和
				out.println(getNum(ot[y]) - getNum(in[y] - 1));
			}
		}
		out.close();
	}

	static int[] in = new int[N + 5]; // in[j] 代表节点j子树的左端点，也就是节点所在端点
	static int[] ot = new int[N + 5];// ot[j] 代表节点子树以哪个右断点
	static int time;

	// 建立dfs序
	static void dfs(int u) {
		in[u] = ++time;
		for (int j = head[u]; j != -1; j = e[j].next) {
			int v = e[j].v;
			dfs(v);
		}
		// 出去的时间
		ot[u] = time;
	}

	static void update(int x, int v) {
		for (int i = x; i <= n; i += i & (-i)) {
			c[i] += v;
		}
	}

	static int getNum(int x) {
		int ans = 0;
		for (int i = x; i > 0; i -= i & (-i)) {
			ans += c[i];
		}
		return ans;
	}
}

class E {
	int v, next;

	public E(int v, int next) {
		this.v = v;
		this.next = next;
	}
}

class Reader {
	BufferedReader buf;
	StringTokenizer tok;

	Reader() {
		buf = new BufferedReader(new InputStreamReader(System.in));
	}

	boolean hasNext() {
		while (tok == null || !tok.hasMoreElements()) {
			try {
				tok = new StringTokenizer(buf.readLine());
			} catch (Exception e) {
				return false;
			}
		}
		return true;
	}

	String next() {
		if (hasNext())
			return tok.nextToken();
		return null;
	}

	int nextInt() {
		return Integer.parseInt(next());
	}

	long nextLong() {
		return Long.parseLong(next());
	}

	double nextDouble() {
		return Double.parseDouble(next());
	}

	BigInteger nextBigInteger() {
		return new BigInteger(next());
	}

	BigDecimal nextBigDecimal() {
		return new BigDecimal(next());
	}
}

来源：https://blog.csdn.net/qq_41280600/article/details/100079666