一,二分图的定义
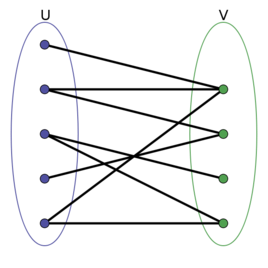
首先,二分图是一个图,这个图的特殊点在于这个图的点可以分成两个集合,并且这个图只在
两个集合间有连边,二分图内部没有连边。
二分图又称作二部图,是图论中的一种特殊模型。 设G=(V,E)是一个无向图,如果顶点V可分割为两个互不相交的子集(A,B)
并且图中的每条边(i,j)所关联的两个顶点i和j分别属于这两个不同的顶点集(i in A,j in B),则称图G为一个二分图。——百度百科
二,二分图的性质
二分图内部不存在奇环(就是边数为奇数的环),可以作为二分图的判定方法。
三,二分图的判定
一般我们采用染色法,给当前顶点染成一种颜色,给另一个顶点染成不同的颜色,如果某一步时条件冲突
就证明当前不是一个二分图,如果全部染色完成没有冲突就证明是一个二分图。
1 #include<cstdio>
2 #include<iostream>
3 #include<cstring>
4 #include<algorithm>
5
6 using namespace std;
7
8 struct node
9 {
10 int ed,nxt;
11 };
12 node edge[2333];
13 int n,m,first[2333],cnt;
14 int color[2333];
15 bool flag;
16
17 inline void add_edge(int s,int e)
18 {
19 cnt++;
20 edge[cnt].ed=e;
21 edge[cnt].nxt=first[s];
22 first[s]=cnt;
23 return;
24 }
25
26 inline void pd(int pos,int c)
27 {
28 color[pos]=c;
29 for(int i=first[pos];i;i=edge[i].nxt)
30 {
31 int e=edge[i].ed;
32 if(color[pos]==color[e]) {flag=false;return;}
33 else if(color[e]==0) pd(e,-c);
34 }
35 }
36
37 int main()
38 {
39 scanf("%d%d",&n,&m);
40 for(int i=1;i<=m;i++)
41 {
42 int s,e;
43 scanf("%d%d",&s,&e);
44 add_edge(s,e);
45 add_edge(e,s);
46 }
47 flag=true;
48 memset(color,0,sizeof(color));
49 for(int i=1;i<=n;i++)
50 {
51 if(!color[i]) pd(i,1);
52 if(!flag)
53 {
54 printf("NO");
55 return 0;
56 }
57 }
58 printf("YES");
59 return 0;
60 }