\(Description\)
给定\(n\)个点,\(m\)条边的无向图(无自环),可以从图中删除一条边,问删除哪些边可以使图变成一个二分图。
\(Input\)
第\(1\)行包含两个整数\(n,m\),分别表示点数和边数。
第\(2~m+1\)行每行两个数\(x,y\),表示有一条边连接点\(x,y\)。
\(Output\)
第一行两个整数,表示能删除的边的个数。
接下来一行按照从小到大的顺序输出能删除的边的编号。
\(Sample Input\)
4 4
1 2
1 3
2 4
3 4
\(Sample Output\)
4
1 2 3 4
\(Hint\)
\(10\%\)的数据,\(n,m<=10\)
\(40\%\)的数据,\(n,m<=1000\)
\(70\%\)的数据,\(n,m<=100000\)
\(100\%\)的数据,\(n,m<=2000000\)
思路
我们看到题目,发现跟判断是否为二分图有关
我们知道,可以通过判断是否存在奇环来判断是否为二分图,而这个判断可以通过\(col\)染色来维护,如果相邻两个节点颜色相同,就是奇环
我们需要删掉一条边使得新图是二分图,就要使所有奇环被破坏,即删除的这条边为所有奇环的共边
于是,我们设\(tot\)为奇环的总个数,设一个数组\(num[u]\),表示经过节点\(u\)的奇环个数,判断\(num[u]=tot\)
但是,我们来看看下面这种情况:
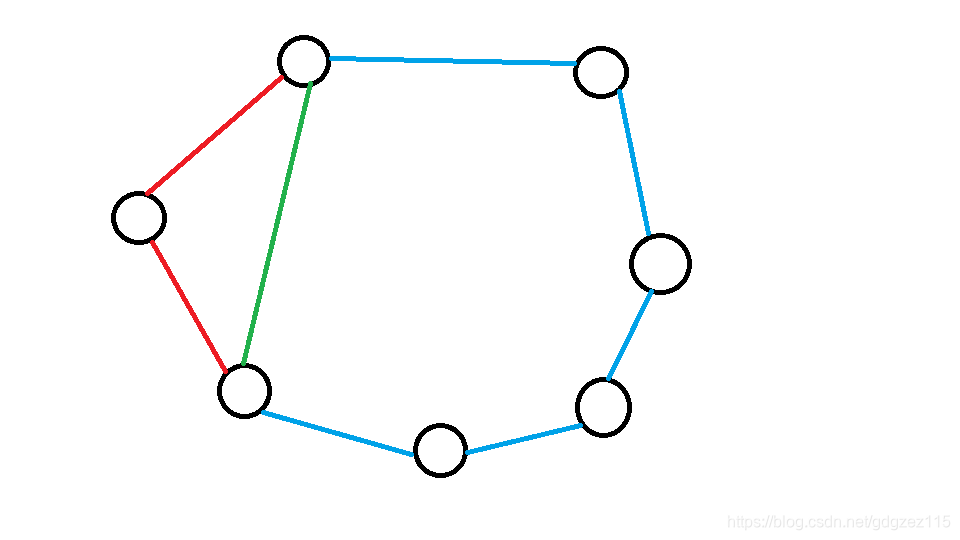
红色边表示奇环的边,蓝色的边表示偶环的边,绿色的边表示两个环的共边
我们可以发现,如果去掉绿的边,则两个环会形成一个新的环,但点数为\(7\),是个奇环!
我们可以得到结论,一个奇环和一个偶环共边,去掉共边,形成的新环是奇环!
于是,我们还要判断一下这个边是不是偶环上的边
代码:
#include<bits/stdc++.h>
using namespace std;
const int N=2000010;
int n,m;
int to[N<<1];
int nxt[N<<1];
int head[N];
int id[N];
int cnt=0;
bool db[N];
int ans[N];
int anstot=0;
int col[N];
int tot=0;
int num[N];
int st[N];
int dfn[N];
bool vis[N];
bool used[N];
int topp=0,ind=0;
void add(int u,int v,int idx)
{
to[++cnt]=v;
nxt[cnt]=head[u];
head[u]=cnt;
id[cnt]=idx;
}
void dfs(int u,int fa)
{
dfn[u]=++ind;
for(int i=head[u];i;i=nxt[i])
{
int v=to[i];
if(dfn[to[i]]>dfn[u]||v==fa)continue;
if(col[v]!=-1)
{
if(col[v]==col[u])//是奇环
{
tot++;
num[id[i]]++;
for(int j=topp;j>0&&to[st[j]]!=v;j--)num[id[st[j]]]++;//奇环更新num
}
else
{
for(int j=topp;j>0&&to[st[j]]!=v;j--)db[id[st[j]]]=1;//偶环打标记
}
}
else
{
col[v]=col[u]^1;//染色
st[++topp]=i;//加入stack
dfs(v,u);
st[topp--]=0;//弹出
}
}
}
void work(int u)
{
vis[u]=1;
for(int i=head[u];i;i=nxt[i])
{
int v=to[i];
if(!used[id[i]]&&((!db[id[i]]&&tot==num[id[i]])||!tot))//used表示是否被统计进答案中
//不是偶环并且是所有奇环的共边或者没有奇环
{
ans[++anstot]=id[i];
used[id[i]]=1;
}
if(!vis[v])work(v);//防止重复访问
}
}
int main()
{
scanf("%d %d",&n,&m);
int a,b;
for(int i=1;i<=m;i++)
{
scanf("%d %d",&a,&b);
add(a,b,i);add(b,a,i);
}
memset(col,-1,sizeof(col));
for(int i=1;i<=n;i++)
{
if(col[i]==-1)
{
tot=0;
col[i]=0;
dfs(i,-1);
work(i);
}
}
sort(ans+1,ans+anstot+1);
printf("%d\n",anstot);
for(int i=1;i<=anstot;i++)printf("%d ",ans[i]);
return 0;
}