洛谷P4525 【模板】自适应辛普森法1与2

洛谷P4525 【模板】自适应辛普森法1

　与P4526【模板】自适应辛普森法2

P4525洛谷传送门

P4525题目描述

计算积分

结果保留至小数点后6位。

数据保证计算过程中分母不为0且积分能够收敛。

输入格式

一行，包含6个实数a,b,c,d,L,R

输出格式

一行，积分值，保留至小数点后6位。

输入输出样例

输入 #1复制

1 2 3 4 5 6

输出 #1复制

2.732937

说明/提示

a,b,c,d∈[-10,10]

-100≤L<R≤100 且 R-L≥1

Solution

今天下午我也不知道为什么要去听这种课，但是又不想在最后几天留下遗憾，所以就听了一些东西，来做（作）做（作）题（死）吧。没想到在几番调试后居然AC了！！！

辛普森公式

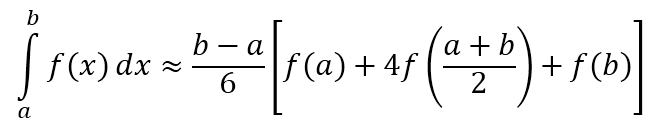
非常优美而又好记！

只有3个系数！

而且，这个东西在计算不超过4次的函数时是非常精准的！

比较适合在于被积函数的原函数不好找的情况下使用！

而且，可以套上递归的模型，使得答案更加准确！

原理

对一段区间进行递归二分，再套用Simpson公式拟合。当整段区间的拟合结果等于（十分接近于）二分区间的两个结果之和时，就是找到了答案。

Code

定义好变量和精度

#include<iostream>  #include<cstdio>  #include<cmath>  #define IL inline  #define re register  using namespace std;  const double eps=1e-12;  double a,b,c,d,L,R;

计算函数f

IL double f(double x)  {      return (c*x+d)/(a*x+b);  }

套用辛普森公式！

IL double simpson(double l,double r)  {      return (r-l)*(f(l)+4*f((l+r)/2.0)+f(r))/6;  }

套用带精度的递归！

double integral(double l,double r)  {      double mid=(l+r)/2,ans=simpson(l,r);      if(fabs(ans-simpson(l,mid)-simpson(mid,r))<eps) return (ans+simpson(l,mid)+simpson(mid,r))/2;      return integral(l,mid)+integral(mid,r);  }

把eps设的再小一点也没又关系哟！再不行，可以考虑使用long double！

主函数部分

int main()  {      cin>>a>>b>>c>>d>>L>>R;      printf("%.6lf",integral(L,R));      return 0;  }

黄字部分：为了使结果更精准，可以将这段区间二分和不二分的答案求加权平均值！

Attention

注意输出六位小数！

递归函数就不要写inline了！不然更容易爆栈！

Simpson公式很好记，考虑背下来？

End

看看下一篇？

洛谷P4526 【模板】自适应辛普森法2

来源：https://www.cnblogs.com/send-off-a-friend/p/11406213.html