一文读懂Python实现张量运算

量子化学计算中除了有大量的线性代数矩阵运算，也有一些张量计算。这些常见的张量计算出现在Fock算符构建、DIIS以及能量对坐标的一、二阶导数上。除此之外张量运算知识也用在Machine Learning以及一些特定的量化计算方法上。张量运算逐渐成为了必备的知识。

现在很多量化计算算法会在Python的生态中快速实现，本文也着重讲Python对张量计算的快速实现。

1. 张量运算的Einstein notation，与numpy实现

在量子化学编程的语义下，我们不必过多的讨论张量是什么的问题，张量就是一个多维数组。例如在Python中：

A = np.random.rand(3,2,5)
B = np.random.rand(3,2,5,6)

‍‍A是一个3×2×5的三维数组(三维张量)，B是一个3×2×5×6的四维数组(四维张量)。接下来我们要对A、B进行运算得到C，C矩阵元定义如下：

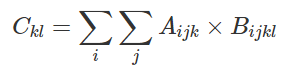
‍‍Einstein notation约定，对于上述求和公式，我们可以省略掉 ∑，即

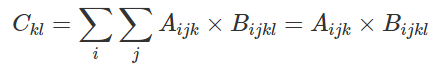
当我们想把Einstein notation复原为正常的式子，需要找到重复的下标，这些下标是出现在 $\sum$ 加和符号下面的‍‍，在A_ijk×B_ijkl中， $i j$ $i j$ 出现了两次，则它们应该是相加。

numpy 提供了一个函数处理张量运算，它基于的正是Einstein notation。函数叫einsum， $C_{k l} = A_{i j k} \times B_{i j k l}$ 这种Einstein notation 可以通过如下方法实现：

只提取下标， $k l = i j k, i j k l$ $k l = i j k, i j k l$
写成字符串，等号变成 →，计算结果数组下标放在右侧，'ijk , ijkl → kl'
写到einsum函数中，被乘函数依序排开。

上述求和，通过如下代码实现,

A = np.random.rand(3,2,5)
B = np.random.rand(3,2,5,6)
C = np.einsum('ijk , ijkl -> kl',A,B)

2. 常见的例子

矩阵的迹

我们有方阵 A，现在想求它的迹tr(A)。

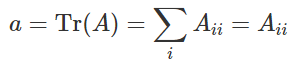
注意，此时求和结果是个数字(零维张量)没有下标，我们要把箭头右侧留空。

A = np.random.rand(5,5)
a = np.einsum('ii -> ',A)
b = np.trace(A)
# a = b

此时np.einsum('ii → ',A) 与np.trace(A)等价。

矩阵乘法

矩阵乘法也可写为Einstein notation。例如我们有A、B两个矩阵，它们做矩阵乘法(matrix multiplication)得到C,

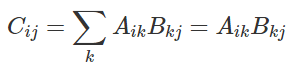
A = np.random.rand(5,6)
B = np.random.rand(6,8)
C = np.einsum('ik ,kj -> ij',A,B)
D = np.dot(A,B)
# C eq. D

此时np.einsum('ik ,kj → ij',A,B) 与np.dot(A,B)等价。

其他的例子，如叉积、Hadamard积、张量转置然后乘积等等都能用einsum方便计算。

3. 量子化学中的举例

在构造Fock算符中，我们会遇到如下运算，

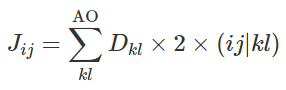
上式是Coulomb对Fock的贡献，它几乎无法转化为矩阵乘法运算，我们只好写循环嵌套，Fock算符的构造比较耗时。D_kl是密度矩阵的矩阵元， ( i j | k l ) 是双电子积分，它是一个四维数组的矩阵元。我们通过如下步骤把它写为einsum求和方式：

1. 写为Einstein Notation：J_ij=D_kl×2×(ij|kl)

2. 下标提取为字符串：'kl, ijkl → ij'

3. 写入函数：2*np.einsum('kl,ijkl → ij',D,I)

通常einsum函数是经过不断优化完善的，运算速度快，避免了我们写低效循环嵌套，并且使代码整洁，对于算法检验，非常合适。不过，我不敢保证einsum是否自动考虑了tensor symmetries, Sparse tensor。 ( i j | k l ) 的对称性大概率没法考虑。另外tensorFlow包里面有自己的einsum函数，可能会更深层次优化。效率问题，还请专业人士指正。

参考资料：

https://rockt.github.io/2018/04/30/einsum
https://en.wikipedia.org/wiki/Einstein_notation
https://docs.scipy.org/doc/numpy/reference/generated/numpy.einsum.html

本文分享自微信公众号 - 量子化学（quantumchemistry）。
如有侵权，请联系 support@oschina.cn 删除。
本文参与“OSC源创计划”，欢迎正在阅读的你也加入，一起分享。

来源：oschina

链接：https://my.oschina.net/u/4589508/blog/4431611

标签

量子

numpy

python