1. 技术文章
  2. 从0开始学算法--数学（4.1矩阵）

从0开始学算法--数学（4.1矩阵）

由 扶醉桌前 提交于 2020-11-03 02:27:48

1，概念

以下词条解释来自百度百科：代数，代数系统，线性代数，矩阵

代数

　　代数是研究数、数量、关系、结构与代数方程（组）的通用解法及其性质的数学分支。初等代数一般在中学时讲授，介绍代数的基本思想：研究当我们对数字作加法或乘法时会发生什么，以及了解变量的概念和如何建立多项式并找出它们的根。代数的研究对象不仅是数字，而是各种抽象化的结构。在其中我们只关心各种关系及其性质，而对于“数本身是什么”这样的问题并不关心。常见的代数结构类型有群、环、域、模、线性空间等。

代数系统

　　非空集合A和A上k个一元或二元运算f1，f2，…，fk组成的系统称为一个代数系统，简称代数，记作(A，f1，f2，…，fk)。由定义可知，一个代数系统需要满足下面3个条件：(1)有一个非空集合A；(2)有一些建立在集合A上的运算；(3)这些运算在集合A上是封闭的。有的书上对代数系统定义时不要求运算的封闭性，而是把具有封闭性的代数系统定义为一个新的概念-广群。

线性代数

　　线性代数是数学的一个分支，它的研究对象是向量，向量空间（或称线性空间），线性变换和有限维的线性方程组。向量空间是现代数学的一个重要课题；因而，线性代数被广泛地应用于抽象代数和泛函分析中；通过解析几何，线性代数得以被具体表示。线性代数的理论已被泛化为算子理论。由于科学研究中的非线性模型通常可以被近似为线性模型，使得线性代数被广泛地应用于自然科学和社会科学中。

矩阵

　　在数学中，矩阵（Matrix）是一个按照长方阵列排列的复数或实数集合 [1]  ，最早来自于方程组的系数及常数所构成的方阵。

2，矩阵的基本运算

矩阵类

矩阵的信息有行数列数和矩阵的内容

struct matrix{
    int n,m;
    long long a[N][M];
    matrix(){//    初始化2*2的单位矩阵
        n=m=2;
        for(int i=0;i<n;i++){
            for(int j=0;j<m;j++){
                a[i][j]=0;
            }
        }
        for(int i=0;i<n;i++){
            a[i][i]=1;
        }
    }
    void clear(){
        //memset(a,0,sizeof(a));
        for(int i=0;i<n;i++){
            for(int j=0;j<m;j++){
                a[i][j]=0;
            }
        }
    }
}

加和减

矩阵的加减运算要抱枕两个矩阵的行数和列数相同

matrix operator+(const matrix &b)const{
    matrix tmp;
    tmp.clear();
    for(int i=0;i<n;i++){
        for(int j=0;j<m;j++){
            tmp.a[i][j]=a[i][j]+b.a[i][j];
        }
    }
    return tmp;
}

乘法

设矩阵乘法的到的结果是矩阵S，则矩阵S的第i行第j个元素是被乘数的第i行元素乘以乘数的第j列元素的求和得到的，也就是说被乘数的列数和乘数的行数相等

matrix operator*(const matrix &b)const{
    matrix tmp;
    tmp.clear();
    for(int i=0;i<n;i++){
        for(int j=0;j<b.m;j++){
            for(int k=0;k<m;k++){
                tmp.a[i][j]=((a[i][k]*b.a[k][j])%mod+tmp.a[i][j])%mod;
            }
        }
    }
    return tmp;
}

因为乘法对矩阵有要求，所以矩阵乘法并不满足交换律，只满足结合律

除法

矩阵并没有除法运算，但是可以求逆，类似在初等数学中数的乘法逆元是他的倒数。矩阵的逆也满足这样的条件，1.矩阵S的逆的逆是矩阵S本身，2.除以矩阵S等于乘以矩阵S的逆

矩阵求逆代码：

vector<double> operator * (vector<double> a,double b){
    int n=a.size();
    vector<double> res(n,0);
    for(int i=0;i<n;i++){
        res[i]=a[i]*b;
    }
    return res;
}

vector<double> operator - (vector<double> a,vector<double> b){
    int n=a.size();
    vector<double> res(n,0);
    for(int i=0;i<n;i++){
        res[i]=a[i]-b[i];
    }
    return res;
}

void get_ni(vector<double>a[],vector<double>b[],int n){//b为初等变换所需要的单位矩阵
    for(int i=0;i<n;i++){
        b[i]=vector<double>(n,0);
    }
    for(int i=0;i<n;i++){//初始化单位矩阵
        b[i][i]=1;
    }
    for(int i=0;i<n;i++){//初等变换
        for(int j=i;j<n;j++){
            if(fabs(a[j][i])>0){
                swap(a[i],a[j]);
                swap(b[i],b[j]);
                break;
            }
        }
        b[i]=b[i]*(1.0/a[i][i]);
        a[i]=a[i]*(1.0/a[i][i]);
        for(int j=0;j<n;j++){
            if(j!=i&&fabs(a[j][i]>0)){
                b[j]=b[j]-b[i]*a[j][i];
                a[j]=a[j]-a[i]*a[j][i];
            }
        }i
    }
}

3.高斯消元

略。。。

4.常系数线性齐次递推

在求解斐波那契数列问题中，如果使用记忆化的技巧，在线性时间内就可以求解第n项斐波那契数是多少。

在矩阵中这个问题如何解决？？

如果可以构造如图所示的矩阵，那么连续给矩阵乘以n个这样的矩阵就可以得到fn。

 

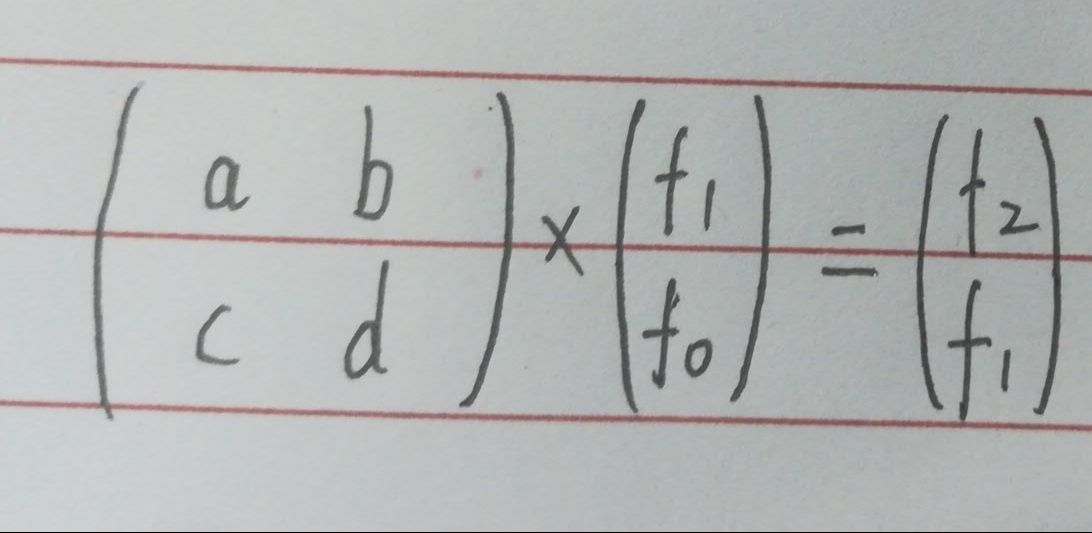
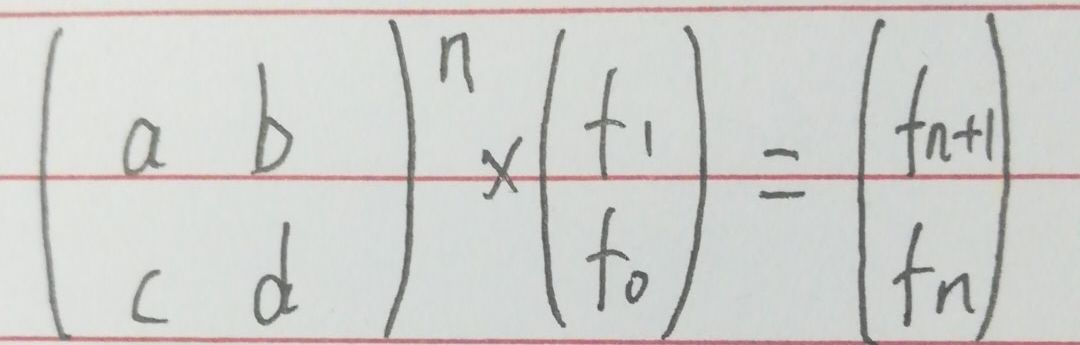
 又因为矩阵满足结合律，所以可以用快速幂的方式，除去矩阵乘法的时间复杂度，O（logn）就可以得到斐波那契数列的第n项。

对于常系数线性齐次递推得到如下结论：

 

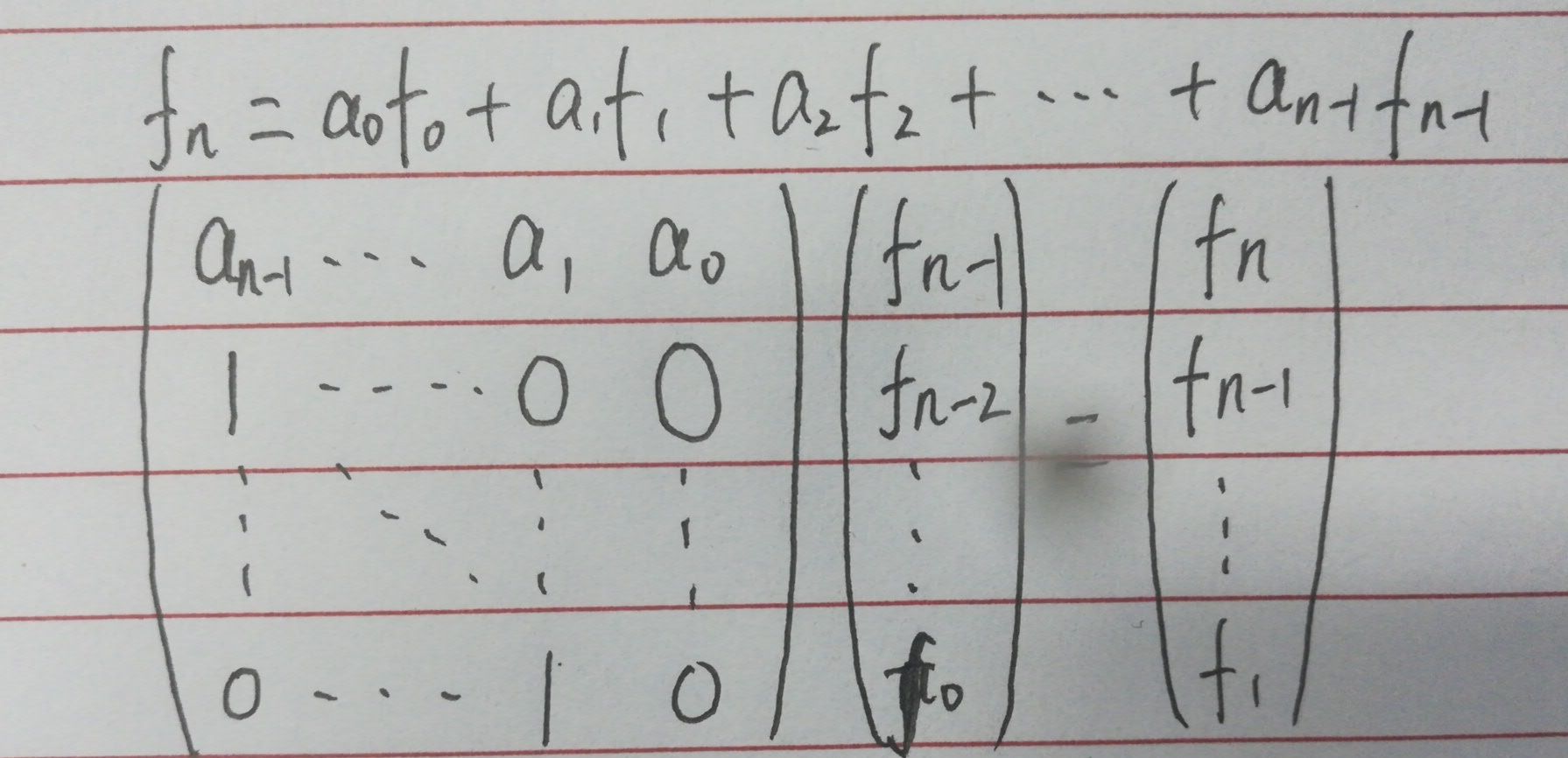
 代码：

const int N=10,M=10;
long long a[10];
long long f[10];

struct matrix{
    int n,m;
    long long a[N][M];
    matrix(){//    初始化2*2的单位矩阵
        n=m=2;
        for(int i=0;i<n;i++){
            for(int j=0;j<m;j++){
                a[i][j]=0;
            }
        }
        for(int i=0;i<n;i++){
            a[i][i]=1;
        }
    }
    void clear(){
        //memset(a,0,sizeof(a));
        for(int i=0;i<n;i++){
            for(int j=0;j<m;j++){
                a[i][j]=0;
            }
        }
    }
    matrix operator+(const matrix &b)const{
        matrix tmp;
        tmp.clear();
        for(int i=0;i<n;i++){
            for(int j=0;j<m;j++){
                tmp.a[i][j]=a[i][j]+b.a[i][j];
            }
        }
        return tmp;
    }
    matrix operator*(const matrix &b)const{
        matrix tmp;
        tmp.clear();
        for(int i=0;i<n;i++){
            for(int j=0;j<b.m;j++){
                for(int k=0;k<m;k++){
                    tmp.a[i][j]=((a[i][k]*b.a[k][j])+tmp.a[i][j]);
                }
            }
        }
        return tmp;
    }
};

matrix pow2(matrix A,int n){
    matrix B;
    while(n>0){
        if(n&1)B=B*A;
        A=A*A;
        n/=2;
    }
    return B;
}

long long solve(long long a[],long long f[],int n,int m){
    matrix A,B;
    A.clear();
    B.clear();
    A.n=B.n=n;
    A.m=n;
    B.m=1;
    for(int i=0;i<n-1;i++){
        A.a[i+1][i]=1;
    }
    for(int i=0;i<n;i++){
        B.a[i][0]=f[n-i-1];
        A.a[0][i]=a[n-i-1];
    }
    A=pow2(A,m);
    B=A*B;
    return B.a[n-1][0];
}

int main(){//求斐波那契数列第m项
    a[0]=1,a[1]=1;      //系数
    f[0]=0,f[1]=1;      //前n项
    int m;
    scanf("%d",&m);
    printf("%lld\n",solve(a,f,2,m));
    return 0;
}

一点心得：（走在路上啃馒头想到的（滑稽）

如果我们的递推式不仅仅是fn=an-1*fn-1+an-2*fn-2+………+a0*f0；这样简单的格式.而是fn=an-1*fn-1+an-2*fn-2+………+a0*f0+c；c是一个常数。那么可以构造如下的矩阵解决一个问题。

 

构造矩阵的方法或许没有多么巧妙，我却收获颇多。

1.矩阵乘法本身其实就在阐述一定的递推关系。

2.如果遇到下图所示矩阵，可分解为两个矩阵。

 

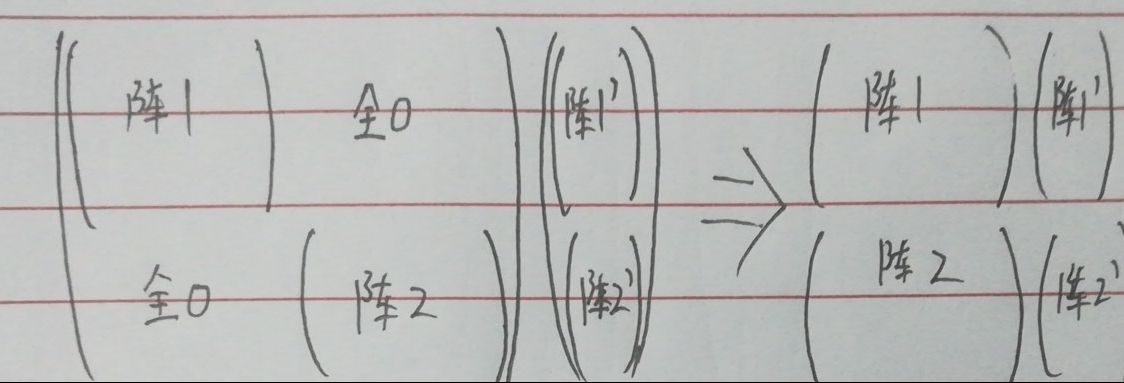
3.如果可以构造出f（n）=n的矩阵，则可以轻易得出fn=an-1*fn-1+an-2*fn-2+………+a0*f0+n的矩阵递推式

同理如果可以构造f（n）=an的矩阵，就可以轻易得出fn=an-1*fn-1+an-2*fn-2+………+a0*f0+an的矩阵递推式

结论：构造出的任意矩阵可以嵌套出一个新的递推式。

 例：

5.递推（第二弹）

例题：POJ3734 Blocks（自我感觉本题阐述了矩阵本身就代表着一定的递推关系）

题意：给出n个排成一列的方块，用红、蓝、绿、黄四种颜色给它们染色，要求出染成红色的方块个数和染成绿色的方块个数同时为偶数的染色方案的个数模10007的值为多少。

从左边开始考虑，染第i个格子的时候有三种情况：

1. 之前i-1个方块中，红色数和绿色数都是偶数，想要满足条件，就要染蓝色或黄色。

2. 之前i-1个方块中，红色数和绿数中有一个为奇数，想要满足条件就要染奇数个对应的颜色。

3. 之前i-1个方块中，红色的方块个数和绿色的方块个数均不是偶数，这时无法满足条件。

如果用a[]，b[]，c[]三个数组表示三种状态。

那么可以得到三个递推式

ai=2*ai-1+bi-1

bi=2*ai-1+2*bi-1+2*ci-1

ci=bi-1+2*ci-1

那么可以得到如下矩阵：

 

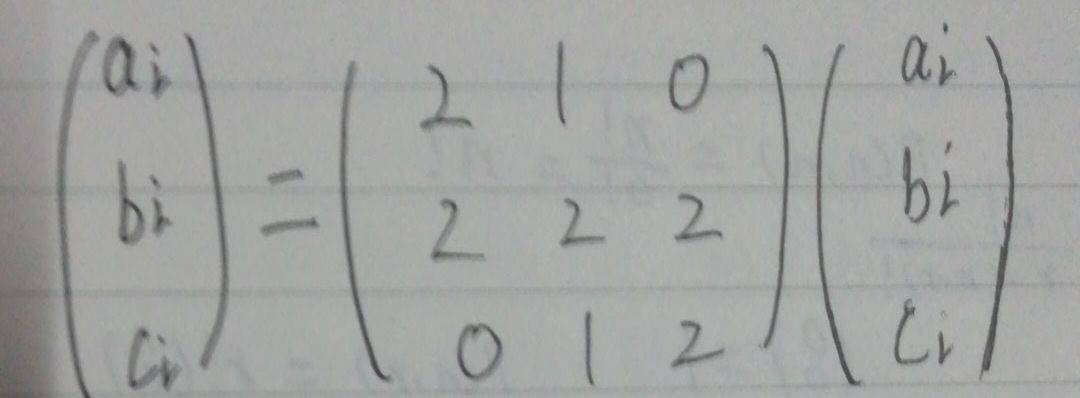
 矩阵快速幂求解即可得到答案.

代码：

#include <iostream>
#include <algorithm>
#include <cstdio>
#include <cstring>

using namespace std;

const int N=10,M=10;
long long a[10];
long long f[10];
const int mod=10007;


struct matrix{
    int n,m;
    long long a[N][M];
    matrix(){//    初始化2*2的单位矩阵
        n=m=3;
        for(int i=0;i<n;i++){
            for(int j=0;j<m;j++){
                a[i][j]=0;
            }
        }
        for(int i=0;i<n;i++){
            a[i][i]=1;
        }
    }
    void clear(){
        //memset(a,0,sizeof(a));
        for(int i=0;i<n;i++){
            for(int j=0;j<m;j++){
                a[i][j]=0;
            }
        }
    }
    matrix operator+(const matrix &b)const{
        matrix tmp;
        tmp.clear();
        for(int i=0;i<n;i++){
            for(int j=0;j<m;j++){
                tmp.a[i][j]=a[i][j]+b.a[i][j];
            }
        }
        return tmp;
    }
    matrix operator*(const matrix &b)const{
        matrix tmp;
        tmp.clear();
        for(int i=0;i<n;i++){
            for(int j=0;j<b.m;j++){
                for(int k=0;k<m;k++){
                    tmp.a[i][j]=((a[i][k]*b.a[k][j])%mod+tmp.a[i][j])%mod;
                }
            }
        }
        return tmp;
    }
};

matrix pow2(matrix A,int n){
    matrix B;
    while(n>0){
        if(n&1)B=B*A;
        A=A*A;
        n/=2;
    }
    return B;
}


long long solve(int n,int m){
    matrix A,B;
    A.clear();
    B.clear();
    A.n=B.n=n;
    A.m=n;
    B.m=1;
    A.a[0][0]=2,A.a[0][1]=1,A.a[0][2]=0;
    A.a[1][0]=A.a[1][1]=A.a[1][2]=2;
    A.a[2][0]=0,A.a[2][1]=1,A.a[2][2]=2;
    B.a[0][0]=1,B.a[0][1]=0,B.a[0][2]=0;
    A=pow2(A,m);
    B=A*B;
    return B.a[0][0];
}

int main(){

    int n;
    scanf("%d",&n);
    for(int i=0;i<n;i++){
        int m;
        scanf("%d",&m);
        printf("%d\n",solve(3,m));
    }
    return 0;
}

 

6.十进制快速幂

例：2019牛客暑期多校训练营（第五场）B题

 

 

 

 

 

 

 

 

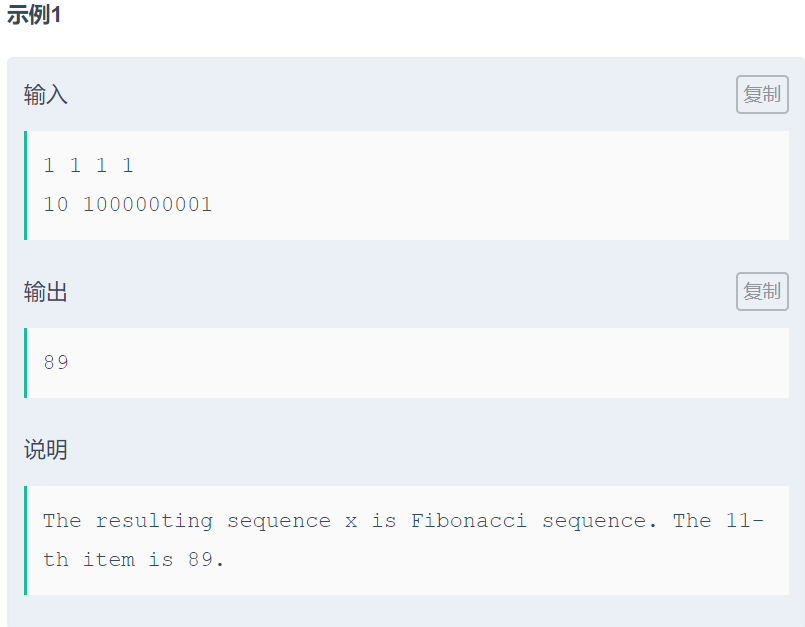
 代码：

#include<algorithm>
#include<iostream>
#include<cstdlib>
#include<fstream>
#include<cstring>
#include<bitset>
#include<cstdio>
#include<time.h>
#include<deque>
#include<queue>
#include<stack>
#include<cmath>
#include<map>
#include<set>
 
using namespace std;
 
long long mod;
const int N=2,M=2;
const int maxnn=1e6+10;
long long a[10];
long long b[10];
char t[maxnn];
 
struct matrix{
    long long a[N][M];
    matrix(){
        for(int i=0;i<2;i++){
            for(int j=0;j<2;j++){
                a[i][j]=0;
            }
        }
        for(int i=0;i<2;i++){
            a[i][i]=1;
        }
    }
    void clear(){
        for(int i=0;i<2;i++){
            for(int j=0;j<2;j++){
                a[i][j]=0;
            }
        }
    }
    matrix operator+(const matrix &b)const{
        matrix tmp;
        tmp.clear();
        for(int i=0;i<2;i++){
            for(int j=0;j<2;j++){
                tmp.a[i][j]=a[i][j]+b.a[i][j];
            }
        }
        return tmp;
    }
    matrix operator*(const matrix &b)const{
        matrix tmp;
        tmp.clear();
        for(int i=0;i<2;i++){
            for(int j=0;j<2;j++){
                for(int k=0;k<2;k++){
                    tmp.a[i][j]=((a[i][k]*b.a[k][j])%mod+tmp.a[i][j])%mod;
                }
            }
        }
        return tmp;
    }
};
 
matrix pow2(matrix A,int n){
    matrix B;
    while(n>0){
        if(n&1)B=B*A;
        A=A*A;
        n/=2;
    }
    return B;
}
 
int main(){
    for(int i=0;i<2;i++){
        scanf("%lld",&a[i]);
    }
    for(int i=1;i>=0;i--){
        scanf("%lld",&b[i]);
    }
    getchar();
    scanf("%s",t);
    getchar();
    scanf("%lld",&mod);
    matrix A;
    A.clear();
    A.a[1][0]=1;
    for(int i=0;i<2;i++){
        A.a[0][i]=b[2-i-1];
    }
    int len=strlen(t);
    matrix D;
    for(int i=len-1;i>=0;i--){
        int x=(t[i]-'0');
        D=D*pow2(A,x);
        A=pow2(A,10);
    }
    long long num=((D.a[1][0]*a[1])%mod+(D.a[1][1]*a[0])%mod)%mod;
    printf("%lld\n",num);
    return 0;
}

 7.补：

一：poj-3233

给定n*n的矩阵A和正整数k和m，求矩阵A的幂的和。S=A+A2+A3+…………+Ak。

输出S的各元素对mod取余后的答案。

n<30,k<109,m<104.

思路一：按线性求出所有A的x次方，加起来，时间复杂度为O（n3k）

思路二：

矩阵的也可以看成一个元素，可以把矩阵元素放在矩阵中加速这个过程。

令Sk=I+A+……+Ak-1（I是单位矩阵）

 

 

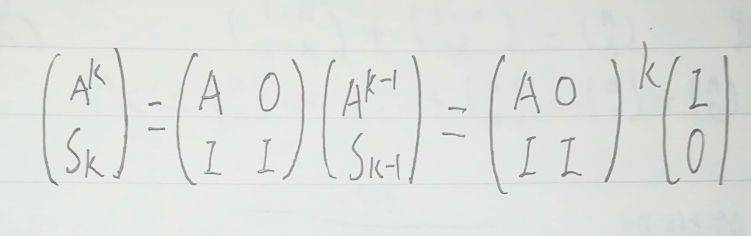
这样就可以在O（n3logk）的时间复杂度内解决问题。

 

标签
人工智能
cstring
易学教程内所有资源均来自网络或用户发布的内容，如有违反法律规定的内容欢迎反馈！
该文章没有解决你所遇到的问题?点击提问,说说你的问题,让更多的人一起探讨吧!