对抗方法过滤数据中的 Bias

标题： Adversarial Filters of Dataset Biases
来源：ICML 2020，Allen Institute for Artificial Intelligence
原文链接： https://arxiv.org/abs/2002.04108

Abstract

大型神经网络模型在语言和视觉基准测试上已经表现出人类的水平，然而在面对对抗性的或 out-of-distribution 样本时，模型的性能会大幅下降。由此引出一个问题：这些模型是否是通过过拟合虚假的数据集 bias 而学会了解决 dataset 而不是基础的 task。文中研究了一种最近提出的方法，AFLITE，它通过对抗过滤这样的数据偏差来减轻普遍高估的机器变现。作者还未 AFLITE 提供了一个理论性的理解，通过将其置于最优 bias 减少的广义框架中。文中提出了大量的支持证据，证明 AFLITE 广泛使用于减少可测量的数据集bias上，并且在过滤好的数据集上训练的模型对 out-of-distribution 的任务有更好的泛化能力。最终，过滤导致模型性能大幅下降（SNLI 从92%下降到62%），但人工的表现依旧很高。因此，本文的工作表明，经过过滤的数据集可以作为升级的 benchmarks，为鲁棒性泛化带来新的研究挑战。

Introduction

在很多受欢迎的AI 基准测试上，大规模神经网络已经达到了超人类的表现，例如图像识别（ImageNet）、自然语言推理（SNLI）以及QA（SQuAD）。然而，这些模型在 out-of-distribution 或对抗样本上的表现却下降得很快，这种现象说明最强的 AI 模型的高性能通常局限于特定的数据集，隐式地做出了一个 closed-world 的假设。相反，对一项任务真正的学习需要一个一般化或 open-world 的假设。阻碍泛化的主要障碍是现有的数据集中存在的虚假 bias —— 输入和输出之间的非预期相关性。这样的偏差或人工产物（artifacts）经常在数据收集或人工标注时被引入。数据集偏差不仅不可避免地会使模型产生偏差，而且会显著夸大模型的性能，导致对 AI 系统的真实能力进行高估。

近期的一些工作已经调查了特定于任务或数据的 bias，包括可视化问答中的语言 bias，ImageNet中的纹理 bias ，以及NLI中的假设依赖问题。这些二研究已经产生了领域特定的算法来解决发现的 bias。然而，这些研究大多遵循自定向下的框架，其中的 bias 消减方法基本上是由研究人员对特定类型的伪偏差的直觉和领域洞察力所引导的。虽然前景看好，但这些方法在根本上受到了算法设计者的人工识别和枚举不想要的bias的限制。

本文的工作研究了 AFLITE，一种选择性的自底向上的算法偏差减少方法。AFLITE 是最近提出的一种尽管很简洁但是能够系统地发现和过滤任何众包数据集的 bias 。AFLITE 采用了一种基于模型的方法，其目标是消除数据中虚假的人工产物（artifacts），这些人工产物超出了人类能够直观识别的范围，但被强大的模型所利用。下图说明了 AFLITE 如何减少 ImageNet 中目标分类的数据集中的bias：

左边为过滤后保留的，右边为滤去的；从热力图可以看到左边的图互相之间的有较大的差异，而右边的相似度很高；经过过滤的例子为图像分类提供了一个更加准确的基准；

文中首次对 AFLITE 进性了理论认识和全面的实证研究。更准确地说，有如下四个贡献：

首先，作者将 AFLITE 用于最优化偏差消减框架中，并证明了 AFLITE 提供了 AFOPT 的使用逼近，AFOPT 是在改框架下理想但是难以计算的偏差消减方法；
其次，作者提出了AFLITE 原文中缺乏的一套广泛的实验，来证明 AFLITE 是否真的移除了数据中那些原始假设的虚假偏差；作者的baseline和分析使用了合成的数据集（更易于控制）和真实数据集；后者包括了NLP和视觉任务：SNLI、MultiNLI数据集用于自然语言推理，QNLI 用于问答，ImageNet 用于目标识别；
三，作者证明了，与在原始有偏差数据集上训练的模型相比，在 AFLITE 过滤后的数据集上训练的模型可以更好地泛化到OOD样本上。这些发现表明，数据集中的虚假偏差人为的是基准测试变得容易，因为模型学会了过度依赖这些偏差，而不是学习更多可迁移的特征，从而损害其OOD 泛化能力；
最后，作者证明了 AFLITE 过滤使得那些被广泛应用的 AI 基准变得更具挑战性；实验观察到即使是最先进的模型，它的变现在所有基准上其域内性能都有显著的下降。例如，最好的模型在 SNLI-AFLITE 上只达到了 63% 的准确率，大约下降了 30%。这些发现尤其令人惊讶，因为 AFLITE 保持了相同的寻来你测试分布，同时保留了一个相当大的训练集。

总之，AFLITE 过滤后的数据集可以作为升级的基准，为模型的鲁棒性泛化提出了新的研究挑战。

AFLITE

在大型数据集数据分布的头部有丰富的数据，其性能有更高的优先级，而数据量少的尾部则有折扣。AFLITE 试图最小化模型利用分布头部偏差的能力，同时保留尾部固有的复杂性。这一节提供了一个正式的框架来研究这种偏差消减技术，揭示 AFLITE 可以看作是最佳偏差消减目标的一种逼近。

Formalization 令 $\Phi$ 表示在数据集 $\mathcal{D}=(X,Y)$ 定义的任何特征表示，AFLITE 寻求一个子集 $S\subset \mathcal{D},\ |S|\ge n$ 能最大限度地适应所揭示的特征；换句话说，对任意同分布的训练集的分割，学习如何最好地利用训练实例上的特征 $\Phi$ 应该不能帮助模型泛化到留存的测试集上。

令 $\mathcal{M}$ 表示一系列能在 $\mathcal{D} = (X,Y)$ 的子集上使用特征 $\Phi (X)$ 训练的分类模型（例如逻辑回归、支持向量机或特殊的神经网络结构）。定义关于模型 $\mathcal{M}$ ， $\Phi$ 的表征偏差为 $\mathcal{R}(\Phi,S,\mathcal{M})$ ，作为 $\mathcal{M}$ 中的模型所能达到的可能的最佳样本外分类精度。给定一个目标最小化缩减的数据集大小，目标是找到一个大小最少为的子集 $S\subset \mathcal{D}$ ：

$\mathop{argmin}_\limits{S\subset \mathcal{D},|S|\ge n}\ \mathcal{R}(\Phi,S,\mathcal{M})\\$

上式对应的是最佳的 bias 消减，被称为 AFOPT，本文中用 $\mathcal{R}(\Phi,S,\mathcal{M})$ 表示期望的分类精度。令 $q:2^S\to[0,1]$ 表示 S 的子集 T=(X^T,Y^T) 的概率分布。接下来以概率 q(T) 随机选择，在 $S \verb|\| T$ 上训练分类器 $M_T\in \mathcal{M}$ ，并在上测试分类器 $f_{M_T}(\Phi(X^T),Y^T)$ 的准确率。上的准确率本身是一个随机变量，因为训练集 $S\verb|\|T$ 是随机采样的。这里将分类准确率的期望值定义为表征偏差：

$\mathcal{R}(\Phi,S,\mathcal{M})\triangleq \mathbb{E}_{T\sim q}[f_{M_T}(\Phi(X^T),Y^T)]\\$

然而，上式中的期望的计算涉及到指数级数量的的不同选择的总和，而且只计算了单个变得非常棘手。为了绕开这个挑战，我们将 $\mathcal{R}(\Phi,S,\mathcal{M})$ 重构为对实例 $i\in S$ 所有的表示偏差的总贡献。重要的是，这种求和只有 |S| 项，计算更有效。作者将其称之为的 可预测的分数 p(i) ，代表了：平均而言，在随机选择的不包含的训练集 $S\verb|\|T$ 上训练的模型 $\mathcal{M}$ 通过特征 $\Phi(x_i)$ 预测得到的。具有高可预测性得分的实例是不可取的，因为可以利用他们的特征来自信地正确预测此类实例。

对于每个 $i\in S$ ，这里将选择一个包含的子集的边缘概率定义为 $q(i)\triangleq\sum_{T\owns i}q(T)$ ，比率 $\frac{q(T)}{q(i)}$ 是在包含了的条件下的概率。令 $f_{M_T}(\Phi(x_i),y_i)$ 为 M_T 在上的分类准确率，然后，我们从 p(i) 的角度将式(2) 写为：

$\begin{align*} &\sum_{T\subset S}q(T)\cdot \frac{1}{|T|}\sum_{i\in T}f_{M_T}(\Phi(x_i),y_i)\\ &=\sum_{T\subset S}\sum_{i\in T}q(T)\cdot\frac{f_{M_T}(\Phi(x_i),y_i)}{|T|}\\ &=\sum_{i\in S}\sum_{T\subset S \\T\owns i}q(T)\cdot\frac{f_{M_T}(\Phi(x_i),y_i)}{|T|}\\ &=\sum_{i\in S}q(i)\sum_{T\subset S \\T\owns i}\frac{q(T)}{q(i)}\frac{f_{M_T}(\Phi(x_i),y_i)}{|T|}\\ &=\sum_{i\in S}q(i)\mathbb{E}_{T\subset S,T\owns i}\bigg[\frac{f_{M_T}(\Phi(x_i),y_i)}{|T|}\bigg]\\ &=\sum_{i\in S}p(i) \end{align*}\\$

其中 p(i) 为：

$p(i)\triangleq q(i)\cdot \mathbb{E}_{T\subset S,T\owns i}\bigg[\frac{f_{M_T}(\Phi(x_i),y_i)}{|T|}\bigg]\\$

尽管重构工作支持任意非零的概率分布是在所有固定大小的 $T\subset S$ 采样上的均匀分布。这使得 |T| 和 q(i) 都是一个固定常量，特别地， $q(i)=\begin{pmatrix}|S|-1\\|T|-1\end{pmatrix}/\begin{pmatrix}|S|\\|T|\end{pmatrix}=\frac{|T|}{|S|}$ ，这产生了一种简化的概率分数 $\widetilde p(i)$ 和一个将重构的式(2) 因式分解后的结果：

$\widetilde p(i)\triangleq \frac{1}{|S|}\mathbb{E}_{T\subset S,T\owns i}[{f_{M_T}(\Phi(x_i),y_i)}]\\ \widetilde p(i)\triangleq \frac{1}{|S|}\mathbb{E}_{T\subset S,T\owns i}[{f_{M_T}(\Phi(x_i),y_i)}]\\$

尽管这种重构减少了式(2) 中指数级的求和，使之成为线性和，但是由于 $S=\mathcal{D}$ 开始，不断迭代，通过给定当前的计算出可预测性分数最高的实例 $\widetilde p(i)$ 并将其滤去。AFLITE 采用了一种贪婪切片方法，也就是说，它识别出个可预测分数最高的实例，将它们从中移除，并且重复这个过程 $\lfloor \frac{|\mathcal{D}|-n}{k}\rfloor$ 次。这个过程可以看成是对 AFOPT 的可计算的实用的近似。附录中，对比了三种启发式方法。所有的情况下，都以一个固定的训练集大小 $|S\verb|\|T|=t$ 。此外，因为通常需要一个更大的过滤好的集合，因此当每个的可预测分数都低于一个预先设置好的 early stopping 阈值 $\tau \in [0,1]$ 时，我们可以提前结束这个迭代的过程（尽管 |S|>n ）。

再以我的理解归纳一下上述的过程：首先我们要知道最根本的目标是找到 $\mathop{argmin}_\limits{S\subset \mathcal{D},|S|\ge n}\ \mathcal{R}(\Phi,S,\mathcal{M})$ ，其中的 $\mathcal{R}$ 是表征 bias，我们需要找到一个 D 的子集，其表征 bias 最小，而 R 的计算需要 S 中以二项分布抽取出子集 $T\subset S$ ，让模型 M 在 S\T 上训练，在 T上测试，计算准确率的期望，这又是一个指数量级的计算。而AFLITE可以算是对这种方法的一种启发式近似，将计算复杂度降低。

Implementation

上图中的算法提供了 AFLITE 的实现。

实际使用中，为了效率， $\Phi(X)$ 是提前计算好的，为了获得 $\Phi(X)$ ，我们需要在低数据的情况下根据学习曲线在一小部分数据上训练第一个 ”warm-up“ 模型，在接下来的实验中将不再使用这些数据，并且，这部分数据大小对应于 AFLITE 的训练大小 t 。、的大小可根据可用的计算预算来决定。

在每个过滤阶段，在 m 个不同的随机划分的数据上训练模型，并收集它们在对应的测试集上的预测结果。对于每个实例，计算它的可预测性得分，及其标签被正确预测的次数与预测的总次数之比。

Synthetic Data Experiments

作者在合成数据上进行了实验评估 AFLITE 能否成功从数据集中移除有可以相关性的数据。作者合成了一个由二维数据点组成的数据集，排列成同心圆，在四个不同的分离层次上，如下图所示：

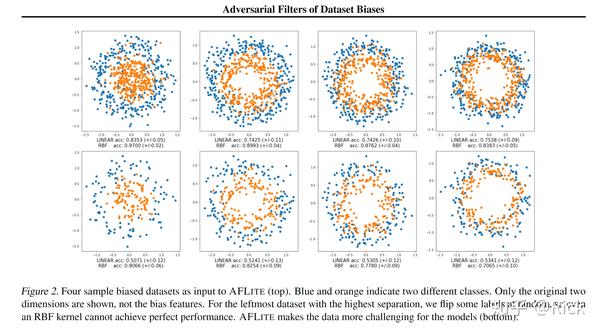
颜色标签代表了数据点所在的圆形区域，显然，一个线性函数并不足以分离这两个类，它需要一个更复杂的分线性模型，例如采用RBF核的SVM。为了模拟数据中的可疑相关性，作者添加了从两个不同的高斯分布中采样的特定类别的人工构造特征(biases)，这些特征只被添加到每个类中75%的数据中，而对于其余的数据，则插入随机特征(噪声)。bias 特征使得任务通过线性函数可解。此外，对于分离程度最大的第一个数据集(图中最左边的)，作者翻转了一些有偏差的样本的标签，使得数据甚至对 RBF 稍微有些不利。两种模型都可以清楚地利用偏差，并在没有偏差的baseline上证明改进的性能。与预期的一样，在应用 AFLITE 后，有偏样本的数量就会大大减少，这使得线性模型的任务再次变得困难，但对于非线性模型依然是可以解决的。

NLP 实验

SNLI数据集中每个实例都由前提-假设句子对组成，任务包括预测假设是否与前提相关联、是否与前提相矛盾或中性。实验使用 RoBERTa-large 作为特征提取器 $\Phi$ ，在原始数据随机采样10%的数据上进行训练。构建三个数据集：原始数据集，过滤后的数据集 $D(\phi_{RoBERTa})$ ，大小与前者相同但是是随机采样的数据集 $D_{182k}$ 。

Out-of-distribution Generalization

如第1节所述，大规模架构常常通过过拟合数据中输入和输出之间的非预期相关性来解决数据集，而不是去学习解决任务，这种依赖会对更一般化的 OOD 样本造成伤害。之前的一些工作中发现在 SNLI 中存在某些注释的人为产物（artifacts）的存在（例如词汇相关性），这使得当前大多数方法在这个任务上变得很容易。这促使开发出了几个可以仔细地控制之前所说的 artifacts的存在的OOD 测试集。文中的实验在四个这样的数据集上进行了测试：HANS、NLI Diagnostic、Stress tests、Adversarial NLI。考虑到这些基准的收集独立于最初的SNLI任务，因此SNLI中的 bias 不太可能继续存在。下表为在三个数据集上实验的结果，模型在SNLI上预训练，然后直接在目标数据集上进行零样本测试：

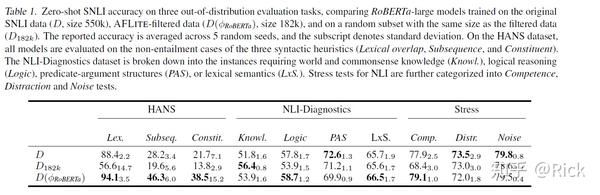
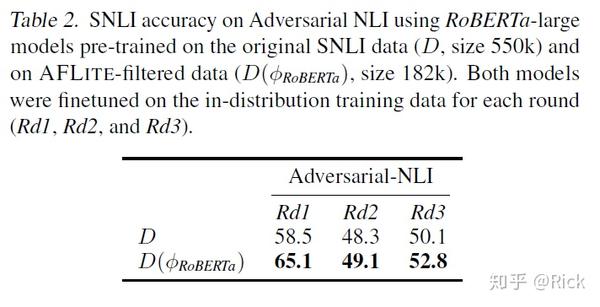
表2中的测试允许评估模型在目标数据上进行fine-tune。

In-distribution Benchmark Re-estimation

此外 AFLITE 还提供了对多个任务上的基准表现更准确的评估。这里简单调低 early-stop 的阈值，滤去更多的有偏置的样本，剩下 92K个训练样本；

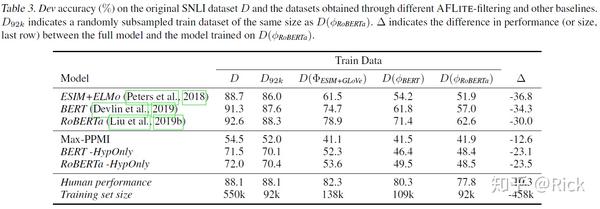
第一个基线使用给定实例中的单词和目标标签之间的点互信息(Point-wise Mutual Information, PMI) 作为其唯一特征，因此它能捕捉到数据中存在的词关联bias的程度；HypOnly 代表只基于假设；

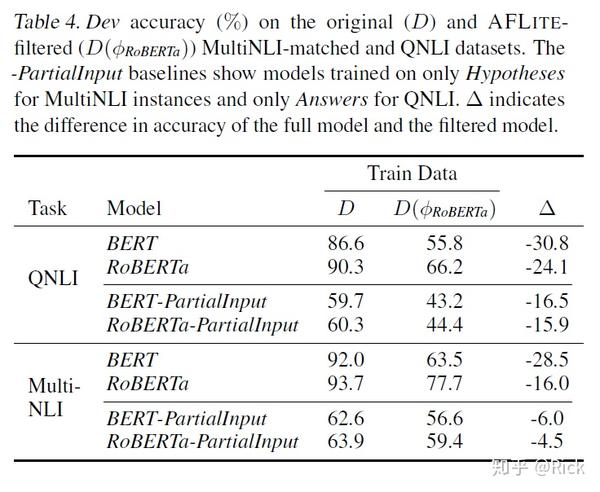
视觉实验

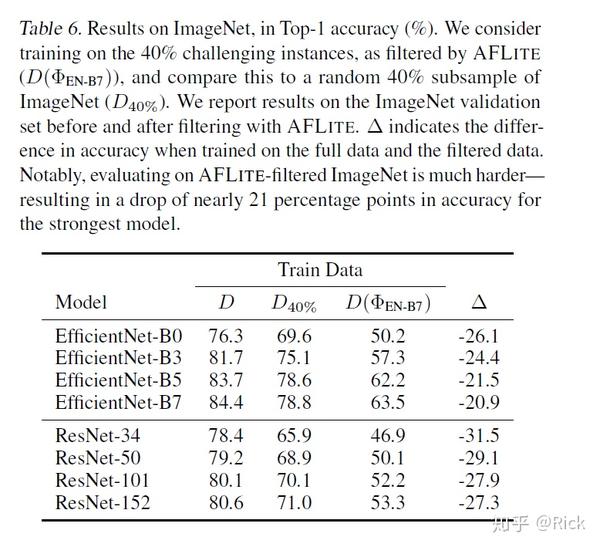
Related Work

Adversarial Filtering 对抗过滤算法与AFLITE很相关，区别主要是两点：1) 用处更广泛（不需要过渡生成数据实例）；2）明显更轻量（每次迭代不需要重新训练模型）；各种 AF 算法的变体被用于创建其它数据集，通过迭代扰动数据集样例，知道目标模型无法匹配结果数据集。这些方法虽然有效，但有三个主要缺陷：1）数据集监管者需要明确的设计一种策略来为给定的实例收集或生成扰动；2）这些方法存在分布bias的风险，鉴别器能够学会区分机器生成的和人类生成的实例；3）每一次迭代都要重新训练模型，计算量大。

AFLITE最初是今年的一篇论文中提出来用于生成 Winogrande数据集的。本文给出了更全面的实验、理论证明以及应用推广。

Data Selection for Debiased Representation 2019有一篇工作 REPAIR，通过数据重采样来移除表征bias，它的动机是学习数据集上的概率分布，这种分布有利于那些对于给定的表征来说很难的实例。对比于AFLITE，REPAIR的使用依赖于寻来你中的分类loss，而不是样本外的泛化准确率。RESOUND（2018）量化了数据集的表征bias，并通过对现有的 C 类数据集进行采样，用它们来装配一个偏差更小的新的K类数据集；数据蒸馏（2018）：它的目的是合成少量的实例来逼近在原始数据上训练的模型；

Learning Objectives for Debiasing 另一个相关的方面是通过设计学习目标来移除数据表征中的bias；将不变风险最小化（Invariant Risk Minimization）作为促进学习跨环境稳定的数据表征的目标；Belinkov等人(2019)提出了一种对抗去除技术，鼓励模型学习不带假设偏差的表征；He等人(2019)提出了 DRiFt，一种去偏算法，该算法首先使用已知的有偏特征学习一个有偏模型，然后训练一个符合有偏模型残差的去偏模型。类似地，Clark等人(2019)提出学习仅使用偏置特征的朴素分类器，与包含更一般特征的其他分类器一起用于集成。Elazar & Goldberg(2018)的研究表明，对抗训练有效地缓解了人口统计学信息泄漏，但在处理文本数据时并不能完全消除人口统计学信息泄漏。

Discussions

这篇文章对AFLITE算法进行了一个论证，针对AFLITE算法，是否可以有一个改进，使之能用于对无监督数据的遴选？文中的方法在debias问题上没能显式找出bias的存在，仅是自动滤去一些可能存在可以相关性的数据，有没有更针对性的方法能去偏但不用滤去数据，甚至可以显式找出这些bias？如文中所述，这个方法为深度学习中很多任务提出了新的benchmark，是否可以 follow 这项工作应用到NLP其它领域中，ACL2020上有一篇引用了这篇文章的论文（Adversarial NLI: A New Benchmark for Natural Language Understanding https://arxiv.org/pdf/1910.14599.pdf，是否可以有一些启发？

来源：oschina

链接：https://my.oschina.net/u/4256940/blog/4656910

标签

人工智能

自然语言处理

神经网络

Benchmark

过拟合