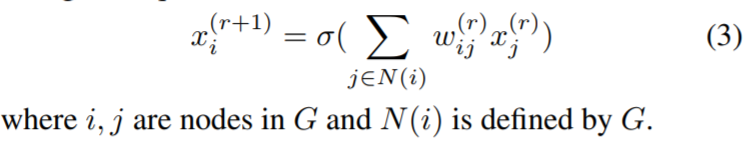Paper:《Graph Neural Networks: A Review of Methods and Applications》翻译与解读
目录
《Graph Neural Networks: A Review of Methods and Applications》翻译与解读
2. Neural Networks as Relational Graphs
2.1. Message Exchange over Graphs
2.2. Fixed-width MLPs as Relational Graphs
2.3. General Neural Networks as Relational Graphs
3. Exploring Relational Graphs
3.1. Selection of Graph Measures
3.2. Design of Graph Generators
3.3. Controlling Computational Budget
4.2. Exploration with Relational Graphs
5.1. A Sweet Spot for Top Neural Networks
5.2. Neural Network Performance as a Smooth Function over Graph Measures
5.3. Consistency across Architectures
5.4. Quickly Identifying a Sweet Spot
5.5. Network Science and Neuroscience Connections
《Graph Neural Networks: A Review of Methods and Applications》翻译与解读

原论文地址:
https://arxiv.org/pdf/2007.06559.pdf
https://arxiv.org/abs/2007.06559
| Comments: | ICML 2020 [Submitted on 13 Jul 2020] |
| Subjects: | Machine Learning (cs.LG); Computer Vision and Pattern Recognition (cs.CV); Social and Information Networks (cs.SI); Machine Learning (stat.ML) |
| Cite as: | arXiv:2007.06559 [cs.LG] (or arXiv:2007.06559v1 [cs.LG] for this version) |
Abstract
| Neural networks are often represented as graphs of connections between neurons. However, despite their wide use, there is currently little understanding of the relationship between the graph structure of the neural network and its predictive performance. Here we systematically investigate how does the graph structure of neural networks affect their predictive performance. To this end, we develop a novel graph-based representation of neural networks called relational graph, where layers of neural network computation correspond to rounds of message exchange along the graph structure. Using this representation we show that: (1) a "sweet spot" of relational graphs leads to neural networks with significantly improved predictive performance; (2) neural network's performance is approximately a smooth function of the clustering coefficient and average path length of its relational graph; (3) our findings are consistent across many different tasks and datasets; (4) the sweet spot can be identified efficiently; (5) top-performing neural networks have graph structure surprisingly similar to those of real biological neural networks. Our work opens new directions for the design of neural architectures and the understanding on neural networks in general. | 神经网络通常用神经元之间的连接图来表示。然而,尽管它们被广泛使用,目前人们对神经网络的图结构与其预测性能之间的关系知之甚少。在这里,我们系统地研究如何图结构的神经网络影响其预测性能。为此,我们开发了一种新的基于图的神经网络表示,称为关系图,其中神经网络计算的层对应于沿着图结构的消息交换轮数。利用这种表示法,我们证明:
|
1. Introduction
| Deep neural networks consist of neurons organized into layers and connections between them. Architecture of a neural network can be captured by its “computational graph” where neurons are represented as nodes and directed edges link neurons in different layers. Such graphical representation demonstrates how the network passes and transforms the information from its input neurons, through hidden layers all the way to the output neurons (McClelland et al., 1986). While it has been widely observed that performance of neural networks depends on their architecture (LeCun et al., 1998; Krizhevsky et al., 2012; Simonyan & Zisserman, 2015; Szegedy et al., 2015; He et al., 2016), there is currently little systematic understanding on the relation between a neural network’s accuracy and its underlying graph structure. This is especially important for the neural architecture search, which today exhaustively searches over all possible connectivity patterns (Ying et al., 2019). From this perspective, several open questions arise:
Establishing such a relation is both scientifically and practically important because it would have direct consequences on designing more efficient and more accurate architectures. It would also inform the design of new hardware architectures that execute neural networks. Understanding the graph structures that underlie neural networks would also advance the science of deep learning. However, establishing the relation between network architecture and its accuracy is nontrivial, because it is unclear how to map a neural network to a graph (and vice versa). The natural choice would be to use computational graph representation but it has many limitations: (1) lack of generality: Computational graphs are constrained by the allowed graph properties, e.g., these graphs have to be directed and acyclic (DAGs), bipartite at the layer level, and single-in-single-out at the network level (Xie et al., 2019). This limits the use of the rich tools developed for general graphs. (2) Disconnection with biology/neuroscience: Biological neural networks have a much richer and less templatized structure (Fornito et al., 2013). There are information exchanges, rather than just single-directional flows, in the brain networks (Stringer et al., 2018). Such biological or neurological models cannot be simply represented by directed acyclic graphs. |
深层神经网络由神经元组成,这些神经元被组织成层,并在层与层之间建立联系。神经网络的结构可以通过它的“计算图”来捕获,其中神经元被表示为节点,有向边连接不同层次的神经元。这样的图形表示演示了网络如何传递和转换来自输入神经元的信息,通过隐藏层一直到输出神经元(McClelland et al., 1986)。虽然已广泛观察到神经网络的性能取决于其结构(LeCun et al., 1998;Krizhevsky等,2012;Simonyan & Zisserman, 2015;Szegedy等,2015;对于神经网络的精度与其底层图结构之间的关系,目前尚无系统的认识。这对于神经结构搜索来说尤为重要,如今,神经结构搜索遍寻所有可能的连通性模式(Ying等人,2019)。从这个角度来看,几个开放的问题出现了:
建立这样的关系在科学上和实践上都很重要,因为它将直接影响到设计更高效、更精确的架构。它还将指导执行神经网络的新硬件架构的设计。理解神经网络的图形结构也将推进深度学习科学。 然而,建立网络架构与其准确度之间的关系并非无关紧要,因为还不清楚如何将神经网络映射到图(反之亦然)。自然选择是使用计算图表示,但它有很多限制:(1)缺乏普遍性:计算图被限制允许图形属性,例如,这些图表必须指导和无环(无进取心的人),在层级别由两部分构成的,single-in-single-out在网络层(谢et al ., 2019)。这限制了为一般图形开发的丰富工具的使用。(2)与生物学/神经科学的分离:生物神经网络具有更丰富的、更少圣殿化的结构(Fornito et al., 2013)。大脑网络中存在着信息交换,而不仅仅是单向流动(Stringer et al., 2018)。这样的生物或神经模型不能简单地用有向无环图来表示。 |
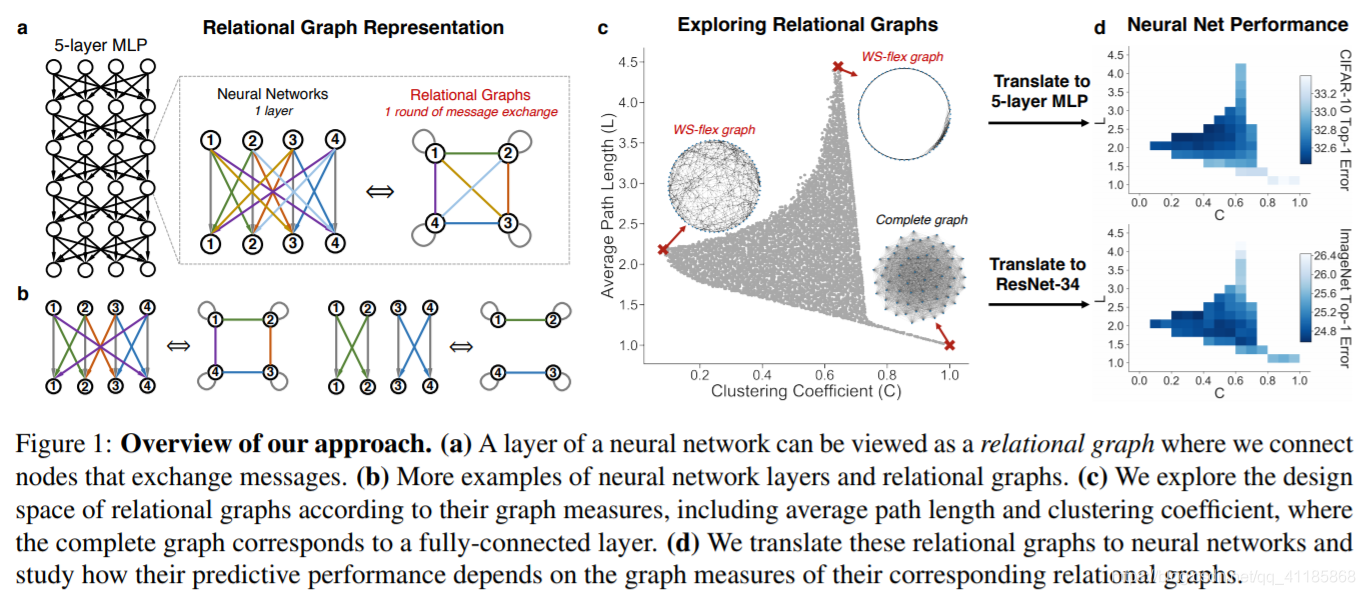
| Here we systematically study the relationship between the graph structure of a neural network and its predictive performance. We develop a new way of representing a neural network as a graph, which we call relational graph. Our key insight is to focus on message exchange, rather than just on directed data flow. As a simple example, for a fixedwidth fully-connected layer, we can represent one input channel and one output channel together as a single node, and an edge in the relational graph represents the message exchange between the two nodes (Figure 1(a)). Under this formulation, using appropriate message exchange definition, we show that the relational graph can represent many types of neural network layers (a fully-connected layer, a convolutional layer, etc.), while getting rid of many constraints of computational graphs (such as directed, acyclic, bipartite, single-in-single-out). One neural network layer corresponds to one round of message exchange over a relational graph, and to obtain deep networks, we perform message exchange over the same graph for several rounds. Our new representation enables us to build neural networks that are richer and more diverse and analyze them using well-established tools of network science (Barabasi & Psfai ´ , 2016). We then design a graph generator named WS-flex that allows us to systematically explore the design space of neural networks (i.e., relation graphs). Based on the insights from neuroscience, we characterize neural networks by the clustering coefficient and average path length of their relational graphs (Figure 1(c)). Furthermore, our framework is flexible and general, as we can translate relational graphs into diverse neural architectures, including Multilayer Perceptrons (MLPs), Convolutional Neural Networks (CNNs), ResNets, etc. with controlled computational budgets (Figure 1(d)). |
本文系统地研究了神经网络的图结构与其预测性能之间的关系。我们提出了一种将神经网络表示为图的新方法,即关系图。我们的重点是关注消息交换,而不仅仅是定向数据流。作为一个简单的例子,对于固定宽度的全连接层,我们可以将一个输入通道和一个输出通道一起表示为单个节点,关系图中的一条边表示两个节点之间的消息交换(图1(a))。在此公式下,利用适当的消息交换定义,我们表明关系图可以表示多种类型的神经网络层(全连通层、卷积层等),同时摆脱了计算图的许多约束(如有向、无环、二部图、单入单出)。一个神经网络层对应于在关系图上进行一轮消息交换,为了获得深度网络,我们在同一图上进行几轮消息交换。我们的新表示使我们能够构建更加丰富和多样化的神经网络,并使用成熟的网络科学工具对其进行分析(Barabasi & Psfai, 2016)。 然后我们设计了一个名为WS-flex的图形生成器,它允许我们系统地探索神经网络的设计空间。关系图)。基于神经科学的见解,我们通过聚类系数和关系图的平均路径长度来描述神经网络(图1(c))。此外,我们的框架是灵活和通用的,因为我们可以将关系图转换为不同的神经结构,包括多层感知器(MLPs)、卷积神经网络(CNNs)、ResNets等,并控制计算预算(图1(d))。 |
| Using standard image classification datasets CIFAR-10 and ImageNet, we conduct a systematic study on how the architecture of neural networks affects their predictive performance. We make several important empirical observations:
Our results have implications for designing neural network architectures, advancing the science of deep learning and improving our understanding of neural networks in general. |
使用标准图像分类数据集CIFAR-10和ImageNet,我们对神经网络的结构如何影响其预测性能进行了系统研究。我们做了几个重要的经验观察:
|
|
Figure 1: Overview of our approach. (a) A layer of a neural network can be viewed as a relational graph where we connect nodes that exchange messages. (b) More examples of neural network layers and relational graphs. (c) We explore the design space of relational graphs according to their graph measures, including average path length and clustering coefficient, where the complete graph corresponds to a fully-connected layer. (d) We translate these relational graphs to neural networks and study how their predictive performance depends on the graph measures of their corresponding relational graphs. 图1:我们方法的概述。(a)神经网络的一层可以看作是一个关系图,在这里我们连接交换消息的节点。(b)神经网络层和关系图的更多例子。(c)我们根据关系图的图度量来探索关系图的设计空间,包括平均路径长度和聚类系数,其中完全图对应一个全连通层。我们将这些关系图转换为神经网络,并研究它们的预测性能如何取决于对应关系图的图度量。 |
2. Neural Networks as Relational Graphs
| To explore the graph structure of neural networks, we first introduce the concept of our relational graph representation and its instantiations. We demonstrate how our representation can capture diverse neural network architectures under a unified framework. Using the language of graph in the context of deep learning helps bring the two worlds together and establish a foundation for our study. | 为了探讨神经网络的图结构,我们首先介绍关系图表示的概念及其实例。我们将演示如何在统一框架下捕获不同的神经网络架构。在深度学习的背景下使用graph语言有助于将这两个世界结合起来,为我们的研究奠定基础。 |
2.1. Message Exchange over Graphs
| We start by revisiting the definition of a neural network from the graph perspective. We define a graph G = (V, E) by its node set V = {v1, ..., vn} and edge set E ⊆ {(vi , vj )|vi , vj ∈ V}. We assume each node v has a node feature scalar/vector xv.
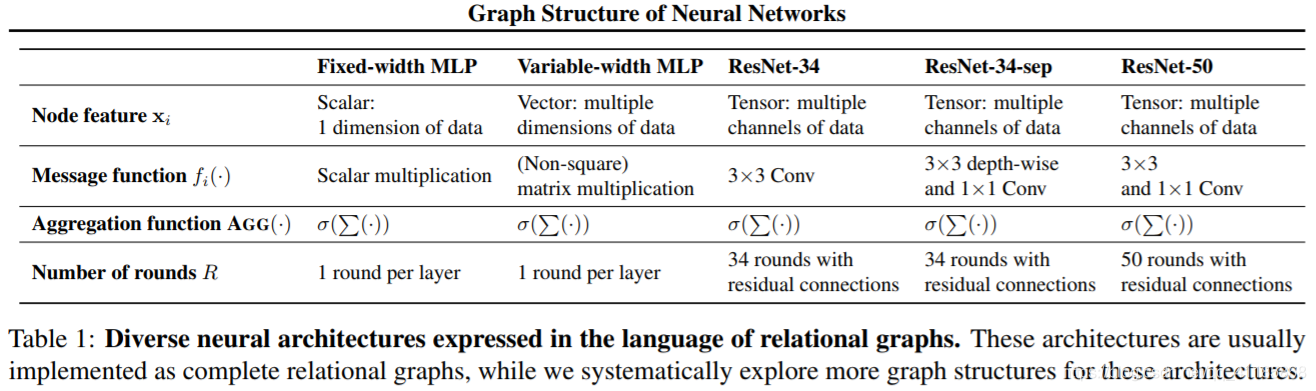
Table 1: Diverse neural architectures expressed in the language of relational graphs. These architectures are usually implemented as complete relational graphs, while we systematically explore more graph structures for these architectures. 表1:用关系图语言表示的各种神经结构。这些架构通常被实现为完整的关系图,而我们系统地为这些架构探索更多的图结构。
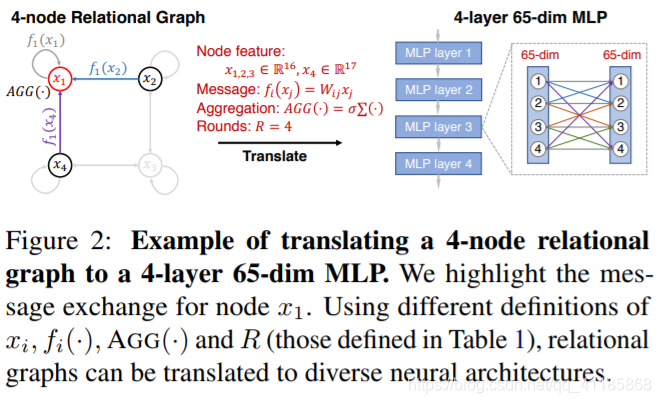
Figure 2: Example of translating a 4-node relational graph to a 4-layer 65-dim MLP. We highlight the message exchange for node x1. Using different definitions of xi , fi(·), AGG(·) and R (those defined in Table 1), relational graphs can be translated to diverse neural architectures. 图2:将4节点关系图转换为4层65-dim MLP的示例。我们将重点介绍节点x1的消息交换。使用xi、fi(·)、AGG(·)和R(表1中定义的)的不同定义,关系图可以转换为不同的神经结构。 |
|
| We call graph G a relational graph, when it is associated with message exchanges between neurons. Specifically, a message exchange is defined by a message function, whose input is a node’s feature and output is a message, and an aggregation function, whose input is a set of messages and output is the updated node feature. At each round of message exchange, each node sends messages to its neighbors, and aggregates incoming messages from its neighbors. Each message is transformed at each edge through a message function f(·), then they are aggregated at each node via an aggregation function AGG(·). Suppose we conduct R rounds of message exchange, then the r-th round of message exchange for a node v can be described as
Equation 1 provides a general definition for message exchange. In the remainder of this section, we discuss how this general message exchange definition can be instantiated as different neural architectures. We summarize the different instantiations in Table 1, and provide a concrete example of instantiating a 4-layer 65-dim MLP in Figure 2. |
我们称图G为关系图,当它与神经元之间的信息交换有关时。具体来说,消息交换由消息函数和聚合函数定义,前者的输入是节点的特性,输出是消息,后者的输入是一组消息,输出是更新后的节点特性。在每一轮消息交换中,每个节点向它的邻居发送消息,并聚合从它的邻居传入的消息。每个消息通过消息函数f(·)在每个边进行转换,然后通过聚合函数AGG(·)在每个节点进行聚合。假设我们进行了R轮的消息交换,那么节点v的第R轮消息交换可以描述为 公式1提供了消息交换的一般定义。在本节的其余部分中,我们将讨论如何将这个通用消息交换定义实例化为不同的神经结构。我们在表1中总结了不同的实例,并在图2中提供了实例化4层65-dim MLP的具体示例。 |
2.2. Fixed-width MLPs as Relational Graphs
| A Multilayer Perceptron (MLP) consists of layers of computation units (neurons), where each neuron performs a weighted sum over scalar inputs and outputs, followed by some non-linearity. Suppose the r-th layer of an MLP takes x (r) as input and x (r+1) as output, then a neuron computes:
|
一个多层感知器(MLP)由多层计算单元(神经元)组成,其中每个神经元执行标量输入和输出的加权和,然后是一些非线性。假设MLP的第r层以x (r)为输入,x (r+1)为输出,则有一个神经元计算: |
| The above discussion reveals that a fixed-width MLP can be viewed as a complete relational graph with a special message exchange function. Therefore, a fixed-width MLP is a special case under a much more general model family, where the message function, aggregation function, and most importantly, the relation graph structure can vary. This insight allows us to generalize fixed-width MLPs from using complete relational graph to any general relational graph G. Based on the general definition of message exchange in Equation 1, we have:
|
上面的讨论表明,可以将固定宽度的MLP视为具有特殊消息交换功能的完整关系图。因此,固定宽度的MLP是更为通用的模型系列中的一种特殊情况,其中消息函数、聚合函数以及最重要的关系图结构可能会发生变化。 这使得我们可以将固定宽度MLPs从使用完全关系图推广到任何一般关系图g。根据公式1中消息交换的一般定义,我们有: |
2.3. General Neural Networks as Relational Graphs
| The graph viewpoint in Equation 3 lays the foundation of representing fixed-width MLPs as relational graphs. In this section, we discuss how we can further generalize relational graphs to general neural networks. Variable-width MLPs as relational graphs. An important design consideration for general neural networks is that layer width often varies through out the network. For example, in CNNs, a common practice is to double the layer width (number of feature channels) after spatial down-sampling.
|
式3中的图点为将定宽MLPs表示为关系图奠定了基础。在这一节中,我们将讨论如何进一步将关系图推广到一般的神经网络。 可变宽度MLPs作为关系图。对于一般的神经网络,一个重要的设计考虑是网络的层宽经常是不同的。例如,在CNNs中,常用的做法是在空间下采样后将层宽(特征通道数)增加一倍。 |
| Note that under this definition, the maximum number of nodes of a relational graph is bounded by the width of the narrowest layer in the corresponding neural network (since the feature dimension for each node must be at least 1).
|
注意,在这个定义下,关系图的最大节点数以对应神经网络中最窄层的宽度为界(因为每个节点的特征维数必须至少为1)。 |
| Modern neural architectures as relational graphs. Finally, we generalize relational graphs to represent modern neural architectures with more sophisticated designs. For example, to represent a ResNet (He et al., 2016), we keep the residual connections between layers unchanged. To represent neural networks with bottleneck transform (He et al., 2016), a relational graph alternatively applies message exchange with 3×3 and 1×1 convolution; similarly, in the efficient computing setup, the widely used separable convolution (Howard et al., 2017; Chollet, 2017) can be viewed as alternatively applying message exchange with 3×3 depth-wise convolution and 1×1 convolution. Overall, relational graphs provide a general representation for neural networks. With proper definitions of node features and message exchange, relational graphs can represent diverse neural architectures, as is summarized in Table 1. |
作为关系图的现代神经结构。最后,我们推广了关系图,用更复杂的设计来表示现代神经结构。例如,为了表示ResNet (He et al., 2016),我们保持层之间的剩余连接不变。为了用瓶颈变换表示神经网络(He et al., 2016),关系图交替应用3×3和1×1卷积的消息交换;同样,在高效的计算设置中,广泛使用的可分离卷积(Howard et al., 2017;Chollet, 2017)可以看作是3×3深度卷积和1×1卷积交替应用消息交换。 总的来说,关系图提供了神经网络的一般表示。通过正确定义节点特性和消息交换,关系图可以表示不同的神经结构,如表1所示。 |
3. Exploring Relational Graphs
| In this section, we describe in detail how we design and explore the space of relational graphs defined in Section 2, in order to study the relationship between the graph structure of neural networks and their predictive performance. Three main components are needed to make progress: (1) graph measures that characterize graph structural properties, (2) graph generators that can generate diverse graphs, and (3) a way to control the computational budget, so that the differences in performance of different neural networks are due to their diverse relational graph structures. |
3.1. Selection of Graph Measures
| Given the complex nature of graph structure, graph measures are often used to characterize graphs. In this paper, we focus on one global graph measure, average path length, and one local graph measure, clustering coefficient. Notably, these two measures are widely used in network science (Watts & Strogatz, 1998) and neuroscience (Sporns, 2003; Bassett & Bullmore, 2006). Specifically, average path length measures the average shortest path distance between any pair of nodes; clustering coefficient measures the proportion of edges between the nodes within a given node’s neighborhood, divided by the number of edges that could possibly exist between them, averaged over all the nodes. There are other graph measures that can be used for analysis, which are included in the Appendix. |
3.2. Design of Graph Generators
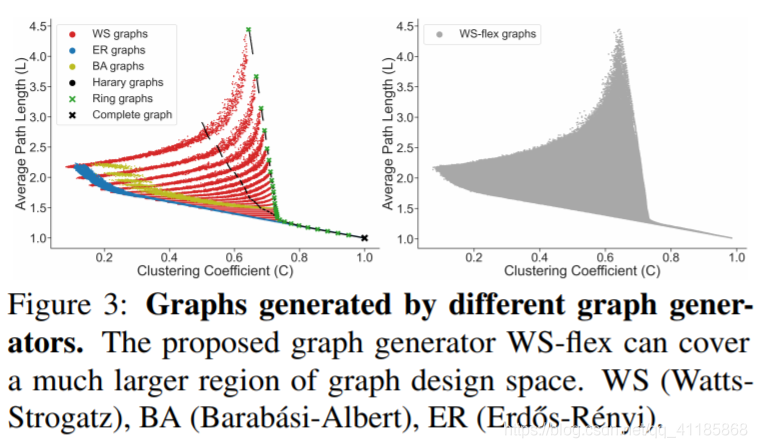
| Given selected graph measures, we aim to generate diverse graphs that can cover a large span of graph measures, using a graph generator. However, such a goal requires careful generator designs: classic graph generators can only generate a limited class of graphs, while recent learning-based graph generators are designed to imitate given exemplar graphs (Kipf & Welling, 2017; Li et al., 2018b; You et al., 2018a;b; 2019a). Limitations of existing graph generators. To illustrate the limitation of existing graph generators, we investigate the following classic graph generators: (1) Erdos-R ˝ enyi ´ (ER) model that can sample graphs with given node and edge number uniformly at random (Erdos & R ˝ enyi ´ , 1960); (2) Watts-Strogatz (WS) model that can generate graphs with small-world properties (Watts & Strogatz, 1998); (3) Barabasi-Albert (BA) model that can generate scale-free ´ graphs (Albert & Barabasi ´ , 2002); (4) Harary model that can generate graphs with maximum connectivity (Harary, 1962); (5) regular ring lattice graphs (ring graphs); (6) complete graphs. For all types of graph generators, we control the number of nodes to be 64, enumerate all possible discrete parameters and grid search over all continuous parameters of the graph generator. We generate 30 random graphs with different random seeds under each parameter setting. In total, we generate 486,000 WS graphs, 53,000 ER graphs, 8,000 BA graphs, 1,800 Harary graphs, 54 ring graphs and 1 complete graph (more details provided in the Appendix). In Figure 3, we can observe that graphs generated by those classic graph generators have a limited span in the space of average path length and clustering coefficient. |
|
| WS-flex graph generator. Here we propose the WS-flex graph generator that can generate graphs with a wide coverage of graph measures; notably, WS-flex graphs almost encompass all the graphs generated by classic random generators mentioned above, as is shown in Figure 3. WSflex generator generalizes WS model by relaxing the constraint that all the nodes have the same degree before random rewiring. Specifically, WS-flex generator is parametrized by node n, average degree k and rewiring probability p. The number of edges is determined as e = bn ∗ k/2c. Specifically, WS-flex generator first creates a ring graph where each node connects to be/nc neighboring nodes; then the generator randomly picks e mod n nodes and connects each node to one closest neighboring node; finally, all the edges are randomly rewired with probability p. We use WS-flex generator to smoothly sample within the space of clustering coefficient and average path length, then sub-sample 3942 graphs for our experiments, as is shown in Figure 1(c). |
3.3. Controlling Computational Budget
| To compare the neural networks translated by these diverse graphs, it is important to ensure that all networks have approximately the same complexity, so that the differences in performance are due to their relational graph structures. We use FLOPS (# of multiply-adds) as the metric. We first compute the FLOPS of our baseline network instantiations (i.e. complete relational graph), and use them as the reference complexity in each experiment. As described in Section 2.3, a relational graph structure can be instantiated as a neural network with variable width, by partitioning dimensions or channels into disjoint set of node features. Therefore, we can conveniently adjust the width of a neural network to match the reference complexity (within 0.5% of baseline FLOPS) without changing the relational graph structures. We provide more details in the Appendix.
|
4. Experimental Setup
| Considering the large number of candidate graphs (3942 in total) that we want to explore, we first investigate graph structure of MLPs on the CIFAR-10 dataset (Krizhevsky, 2009) which has 50K training images and 10K validation images. We then further study the larger and more complex task of ImageNet classification (Russakovsky et al., 2015), which consists of 1K image classes, 1.28M training images and 50K validation images. |
4.1. Base Architectures
| For CIFAR-10 experiments, We use a 5-layer MLP with 512 hidden units as the baseline architecture. The input of the MLP is a 3072-d flattened vector of the (32×32×3) image, the output is a 10-d prediction. Each MLP layer has a ReLU non-linearity and a BatchNorm layer (Ioffe & Szegedy, 2015). We train the model for 200 epochs with batch size 128, using cosine learning rate schedule (Loshchilov & Hutter, 2016) with an initial learning rate of 0.1 (annealed to 0, no restarting). We train all MLP models with 5 different random seeds and report the averaged results. | |
| For ImageNet experiments, we use three ResNet-family architectures, including (1) ResNet-34, which only consists of basic blocks of 3×3 convolutions (He et al., 2016); (2) ResNet-34-sep, a variant where we replace all 3×3 dense convolutions in ResNet-34 with 3×3 separable convolutions (Chollet, 2017); (3) ResNet-50, which consists of bottleneck blocks (He et al., 2016) of 1×1, 3×3, 1×1 convolutions. Additionally, we use EfficientNet-B0 architecture (Tan & Le, 2019) that achieves good performance in the small computation regime. Finally, we use a simple 8- layer CNN with 3×3 convolutions. The model has 3 stages with [64, 128, 256] hidden units. Stride-2 convolutions are used for down-sampling. The stem and head layers are the same as a ResNet. We train all the ImageNet models for 100 epochs using cosine learning rate schedule with initial learning rate of 0.1. Batch size is 256 for ResNetfamily models and 512 for EfficientNet-B0. We train all ImageNet models with 3 random seeds and report the averaged performance. All the baseline architectures have a complete relational graph structure. The reference computational complexity is 2.89e6 FLOPS for MLP, 3.66e9 FLOPS for ResNet-34, 0.55e9 FLOPS for ResNet-34-sep, 4.09e9 FLOPS for ResNet-50, 0.39e9 FLOPS for EffcientNet-B0, and 0.17e9 FLOPS for 8-layer CNN. Training an MLP model roughly takes 5 minutes on a NVIDIA Tesla V100 GPU, and training a ResNet model on ImageNet roughly takes a day on 8 Tesla V100 GPUs with data parallelism. We provide more details in Appendix. | |
|
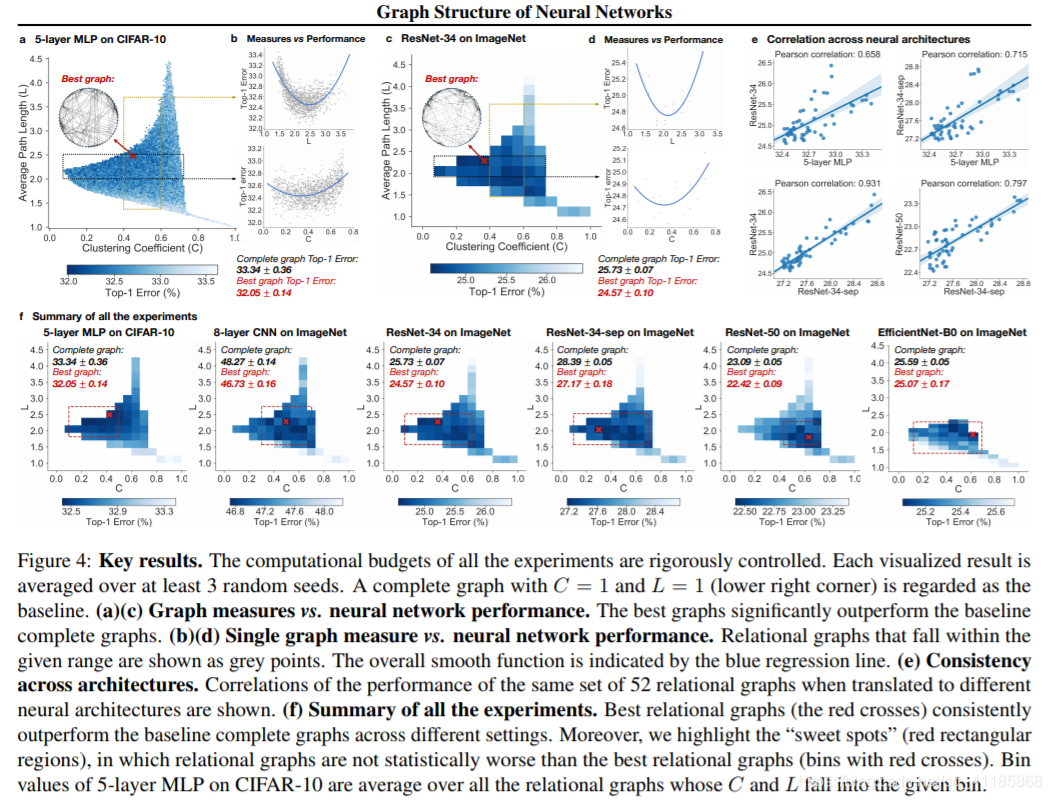
Figure 4: Key results. The computational budgets of all the experiments are rigorously controlled. Each visualized result is averaged over at least 3 random seeds. A complete graph with C = 1 and L = 1 (lower right corner) is regarded as the baseline. (a)(c) Graph measures vs. neural network performance. The best graphs significantly outperform the baseline complete graphs. (b)(d) Single graph measure vs. neural network performance. Relational graphs that fall within the given range are shown as grey points. The overall smooth function is indicated by the blue regression line. (e) Consistency across architectures. Correlations of the performance of the same set of 52 relational graphs when translated to different neural architectures are shown. (f) Summary of all the experiments. Best relational graphs (the red crosses) consistently outperform the baseline complete graphs across different settings. Moreover, we highlight the “sweet spots” (red rectangular regions), in which relational graphs are not statistically worse than the best relational graphs (bins with red crosses). Bin values of 5-layer MLP on CIFAR-10 are average over all the relational graphs whose C and L fall into the given bin |
4.2. Exploration with Relational Graphs
| For all the architectures, we instantiate each sampled relational graph as a neural network, using the corresponding definitions outlined in Table 1. Specifically, we replace all the dense layers (linear layers, 3×3 and 1×1 convolution layers) with their relational graph counterparts. We leave the input and output layer unchanged and keep all the other designs (such as down-sampling, skip-connections, etc.) intact. We then match the reference computational complexity for all the models, as discussed in Section 3.3. |
|
| For CIFAR-10 MLP experiments, we study 3942 sampled relational graphs of 64 nodes as described in Section 3.2. For ImageNet experiments, due to high computational cost, we sub-sample 52 graphs uniformly from the 3942 graphs. Since EfficientNet-B0 is a small model with a layer that has only 16 channels, we can not reuse the 64-node graphs sampled for other setups. We re-sample 48 relational graphs with 16 nodes following the same procedure in Section 3. |
5. Results
| In this section, we summarize the results of our experiments and discuss our key findings. We collect top-1 errors for all the sampled relational graphs on different tasks and architectures, and also record the graph measures (average path length L and clustering coefficient C) for each sampled graph. We present these results as heat maps of graph measures vs. predictive performance (Figure 4(a)(c)(f)). |
5.1. A Sweet Spot for Top Neural Networks
| Overall, the heat maps of graph measures vs. predictive performance (Figure 4(f)) show that there exist graph structures that can outperform the complete graph (the pixel on bottom right) baselines. The best performing relational graph can outperform the complete graph baseline by 1.4% top-1 error on CIFAR-10, and 0.5% to 1.2% for models on ImageNet. Notably, we discover that top-performing graphs tend to cluster into a sweet spot in the space defined by C and L (red rectangles in Figure 4(f)). We follow these steps to identify a sweet spot: (1) we downsample and aggregate the 3942 graphs in Figure 4(a) into a coarse resolution of 52 bins, where each bin records the performance of graphs that fall into the bin; (2) we identify the bin with best average performance (red cross in Figure 4(f)); (3) we conduct onetailed t-test over each bin against the best-performing bin, and record the bins that are not significantly worse than the best-performing bin (p-value 0.05 as threshold). The minimum area rectangle that covers these bins is visualized as a sweet spot. For 5-layer MLP on CIFAR-10, the sweet spot is C ∈ [0.10, 0.50], L ∈ [1.82, 2.75]. |
5.2. Neural Network Performance as a Smooth Function over Graph Measures
| In Figure 4(f), we observe that neural network’s predictive performance is approximately a smooth function of the clustering coefficient and average path length of its relational graph. Keeping one graph measure fixed in a small range (C ∈ [0.4, 0.6], L ∈ [2, 2.5]), we visualize network performances against the other measure (shown in Figure 4(b)(d)). We use second degree polynomial regression to visualize the overall trend. We observe that both clustering coefficient and average path length are indicative of neural network performance, demonstrating a smooth U-shape correlation |
5.3. Consistency across Architectures
|
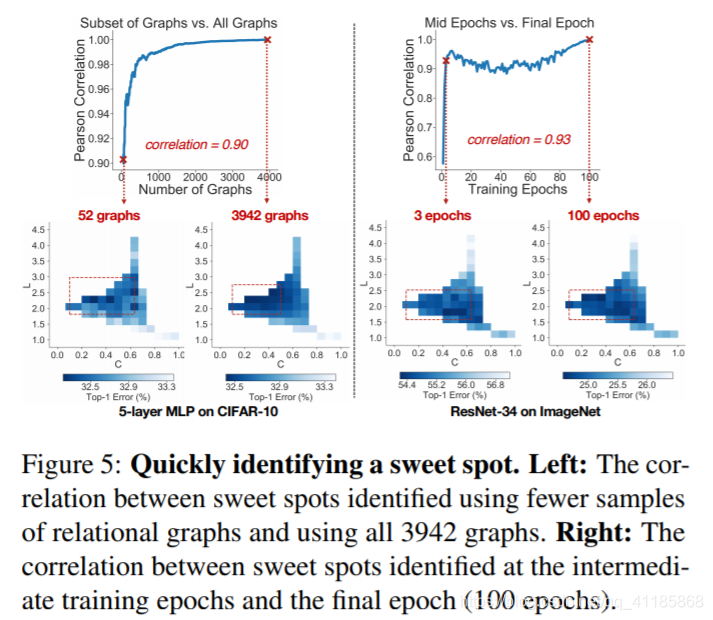
Figure 5: Quickly identifying a sweet spot. Left: The correlation between sweet spots identified using fewer samples of relational graphs and using all 3942 graphs. Right: The correlation between sweet spots identified at the intermediate training epochs and the final epoch (100 epochs). |
|
| Given that relational graph defines a shared design space across various neural architectures, we observe that relational graphs with certain graph measures may consistently perform well regardless of how they are instantiated. Qualitative consistency. We visually observe in Figure 4(f) that the sweet spots are roughly consistent across different architectures. Specifically, if we take the union of the sweet spots across architectures, we have C ∈ [0.43, 0.50], L ∈ [1.82, 2.28] which is the consistent sweet spot across architectures. Moreover, the U-shape trends between graph measures and corresponding neural network performance, shown in Figure 4(b)(d), are also visually consistent. Quantitative consistency. To further quantify this consistency across tasks and architectures, we select the 52 bins in the heat map in Figure 4(f), where the bin value indicates the average performance of relational graphs whose graph measures fall into the bin range. We plot the correlation of the 52 bin values across different pairs of tasks, shown in Figure 4(e). We observe that the performance of relational graphs with certain graph measures correlates across different tasks and architectures. For example, even though a ResNet-34 has much higher complexity than a 5-layer MLP, and ImageNet is a much more challenging dataset than CIFAR-10, a fixed set relational graphs would perform similarly in both settings, indicated by a Pearson correlation of 0.658 (p-value < 10−8 ). |
5.4. Quickly Identifying a Sweet Spot
| Training thousands of relational graphs until convergence might be computationally prohibitive. Therefore, we quantitatively show that a sweet spot can be identified with much less computational cost, e.g., by sampling fewer graphs and training for fewer epochs. How many graphs are needed? Using the 5-layer MLP on CIFAR-10 as an example, we consider the heat map over 52 bins in Figure 4(f) which is computed using 3942 graph samples. We investigate if a similar heat map can be produced with much fewer graph samples. Specifically, we sub-sample the graphs in each bin while making sure each bin has at least one graph. We then compute the correlation between the 52 bin values computed using all 3942 graphs and using sub-sampled fewer graphs, as is shown in Figure 5 (left). We can see that bin values computed using only 52 samples have a high 0.90 Pearson correlation with the bin values computed using full 3942 graph samples. This finding suggests that, in practice, much fewer graphs are needed to conduct a similar analysis. |
|
 |
5.5. Network Science and Neuroscience Connections
| Network science. The average path length that we measure characterizes how well information is exchanged across the network (Latora & Marchiori, 2001), which aligns with our definition of relational graph that consists of rounds of message exchange. Therefore, the U-shape correlation in Figure 4(b)(d) might indicate a trade-off between message exchange efficiency (Sengupta et al., 2013) and capability of learning distributed representations (Hinton, 1984). Neuroscience. The best-performing relational graph that we discover surprisingly resembles biological neural networks, as is shown in Table 2 and Figure 6. The similarities are in two-fold: (1) the graph measures (L and C) of top artificial neural networks are highly similar to biological neural networks; (2) with the relational graph representation, we can translate biological neural networks to 5-layer MLPs, and found that these networks also outperform the baseline complete graphs. While our findings are preliminary, our approach opens up new possibilities for interdisciplinary research in network science, neuroscience and deep learning. |
6. Related Work
| Neural network connectivity. The design of neural network connectivity patterns has been focused on computational graphs at different granularity: the macro structures, i.e. connectivity across layers (LeCun et al., 1998; Krizhevsky et al., 2012; Simonyan & Zisserman, 2015; Szegedy et al., 2015; He et al., 2016; Huang et al., 2017; Tan & Le, 2019), and the micro structures, i.e. connectivity within a layer (LeCun et al., 1998; Xie et al., 2017; Zhang et al., 2018; Howard et al., 2017; Dao et al., 2019; Alizadeh et al., 2019). Our current exploration focuses on the latter, but the same methodology can be extended to the macro space. Deep Expander Networks (Prabhu et al., 2018) adopt expander graphs to generate bipartite structures. RandWire (Xie et al., 2019) generates macro structures using existing graph generators. However, the statistical relationships between graph structure measures and network predictive performances were not explored in those works. Another related work is Cross-channel Communication Networks (Yang et al., 2019) which aims to encourage the neuron communication through message passing, where only a complete graph structure is considered. | |
| Neural architecture search. Efforts on learning the connectivity patterns at micro (Ahmed & Torresani, 2018; Wortsman et al., 2019; Yang et al., 2018), or macro (Zoph & Le, 2017; Zoph et al., 2018) level mostly focus on improving learning/search algorithms (Liu et al., 2018; Pham et al., 2018; Real et al., 2019; Liu et al., 2019). NAS-Bench101 (Ying et al., 2019) defines a graph search space by enumerating DAGs with constrained sizes (≤ 7 nodes, cf. 64-node graphs in our work). Our work points to a new path: instead of exhaustively searching over all the possible connectivity patterns, certain graph generators and graph measures could define a smooth space where the search cost could be significantly reduced. |
7. Discussions
| Hierarchical graph structure of neural networks. As the first step in this direction, our work focuses on graph structures at the layer level. Neural networks are intrinsically hierarchical graphs (from connectivity of neurons to that of layers, blocks, and networks) which constitute a more complex design space than what is considered in this paper. Extensive exploration in that space will be computationally prohibitive, but we expect our methodology and findings to generalize. Efficient implementation. Our current implementation uses standard CUDA kernels thus relies on weight masking, which leads to worse wall-clock time performance compared with baseline complete graphs. However, the practical adoption of our discoveries is not far-fetched. Complementary to our work, there are ongoing efforts such as block-sparse kernels (Gray et al., 2017) and fast sparse ConvNets (Elsen et al., 2019) which could close the gap between theoretical FLOPS and real-world gains. Our work might also inform the design of new hardware architectures, e.g., biologicallyinspired ones with spike patterns (Pei et al., 2019). |
|
| Prior vs. Learning. We currently utilize the relational graph representation as a structural prior, i.e., we hard-wire the graph structure on neural networks throughout training. It has been shown that deep ReLU neural networks can automatically learn sparse representations (Glorot et al., 2011). A further question arises: without imposing graph priors, does any graph structure emerge from training a (fully-connected) neural network?
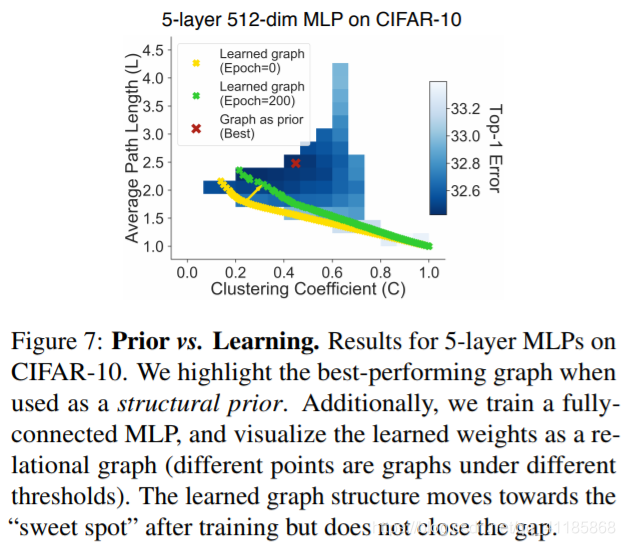
Figure 7: Prior vs. Learning. Results for 5-layer MLPs on CIFAR-10. We highlight the best-performing graph when used as a structural prior. Additionally, we train a fullyconnected MLP, and visualize the learned weights as a relational graph (different points are graphs under different thresholds). The learned graph structure moves towards the “sweet spot” after training but does not close the gap. |
|
| As a preliminary exploration, we “reverse-engineer” a trained neural network and study the emerged relational graph structure. Specifically, we train a fully-connected 5-layer MLP on CIFAR-10 (the same setup as in previous experiments). We then try to infer the underlying relational graph structure of the network via the following steps: (1) to get nodes in a relational graph, we stack the weights from all the hidden layers and group them into 64 nodes, following the procedure described in Section 2.2; (2) to get undirected edges, the weights are summed by their transposes; (3) we compute the Frobenius norm of the weights as the edge value; (4) we get a sparse graph structure by binarizing edge values with a certain threshold. We show the extracted graphs under different thresholds in Figure 7. As expected, the extracted graphs at initialization follow the patterns of E-R graphs (Figure 3(left)), since weight matrices are randomly i.i.d. initialized. Interestingly, after training to convergence, the extracted graphs are no longer E-R random graphs and move towards the sweet spot region we found in Section 5. Note that there is still a gap between these learned graphs and the best-performing graph imposed as a structural prior, which might explain why a fully-connected MLP has inferior performance. In our experiments, we also find that there are a few special cases where learning the graph structure can be superior (i.e., when the task is simple and the network capacity is abundant). We provide more discussions in the Appendix. Overall, these results further demonstrate that studying the graph structure of a neural network is crucial for understanding its predictive performance. |
|
| Unified view of Graph Neural Networks (GNNs) and general neural architectures. The way we define neural networks as a message exchange function over graphs is partly inspired by GNNs (Kipf & Welling, 2017; Hamilton et al., 2017; Velickovi ˇ c et al. ´ , 2018). Under the relational graph representation, we point out that GNNs are a special class of general neural architectures where: (1) graph structure is regarded as the input instead of part of the neural architecture; consequently, (2) message functions are shared across all the edges to respect the invariance properties of the input graph. Concretely, recall how we define general neural networks as relational graphs:
Therefore, our work offers a unified view of GNNs and general neural architecture design, which we hope can bridge the two communities and inspire new innovations. On one hand, successful techniques in general neural architectures can be naturally introduced to the design of GNNs, such as separable convolution (Howard et al., 2017), group normalization (Wu & He, 2018) and Squeeze-and-Excitation block (Hu et al., 2018); on the other hand, novel GNN architectures (You et al., 2019b; Chen et al., 2019) beyond the commonly used paradigm (i.e., Equation 6) may inspire more advanced neural architecture designs. |
8. Conclusion
| In sum, we propose a new perspective of using relational graph representation for analyzing and understanding neural networks. Our work suggests a new transition from studying conventional computation architecture to studying graph structure of neural networks. We show that well-established graph techniques and methodologies offered in other science disciplines (network science, neuroscience, etc.) could contribute to understanding and designing deep neural networks. We believe this could be a fruitful avenue of future research that tackles more complex situations. |
Acknowledgments
| This work is done during Jiaxuan You’s internship at Facebook AI Research. Jure Leskovec is a Chan Zuckerberg Biohub investigator. The authors thank Alexander Kirillov, Ross Girshick, Jonathan Gomes Selman, Pan Li for their helpful discussions. |
来源:oschina
链接:https://my.oschina.net/u/4350591/blog/4406296