详解斜率优化
斜率优化的话前几个月学过一次,然后感觉会了,结果今天遇到个题,比赛时花了1h硬敲没怼出来,然后又去看了看人家的讲解,加上自己疯狂yy,才发现(原来很水嘛)上次只是略懂皮毛。这是开通博客园的第一篇博客,记录一下斜率优化,顺便为自己以后复习做准备。
前置芝士:
dp(废话)
单调队列
初二数学(起码知道笛卡尔坐标系和一次函数吧QWQ)
一定的数形结合能力
那么我们开始吧。
引例(这里推出今天怼了好久没搞出来的水题)
我们需要将一个文件复制到n个服务器上,这些服务器的编号为S1, S2, …, Sn。
首先,我们可以选择一些服务器,直接把文件复制到它们中;将文件复制到服务器Si上,需要花费ci > 0的置放费用。对于没有直接被复制文件的服务器Si来说,它依次向后检查Si+1, Si+2, …直到找到一台服务器Sj:Sj中的文件是通过直接复制得到的,于是Si从Sj处间接复制得到该文件,这种复制方式的读取费用是j – i(注意j>i)。另外,Sn中的文件必须是通过直接复制得到的,因为它不可能间接的通过别的服务器进行复制。我们设计一种复制方案,即对每一台服务器确定它是通过直接还是间接的方式进行复制(Sn只能通过直接方式),最终使每一台服务器都得到文件,且总花费最小。
60% n<=1000
100% n<=1000000
额,说了一大坨,大概意思就是说每个点要不花费c[i]直接复制,要不找到后面最近的是直接花费的j,然后花费j-i来复制。
然后方程是十分显然的,我们设f[i]表示1到i这些点,i花费c[i]直接复制时的最小费用,然后答案就是f[n]了
方程就是:
f[i]=a[i]+min{f[j]+(i-j)*(i-j-1)/2}(0<=j<i)
口糊一下就是我们枚举上一个直接复制的点j,然后j+1到i-1的点全都往i间接复制,这个显然的等差数列嘛。
好了,到这里成功的拿到了60分的好成绩QWQ
那么都到这了是吧,当然要继续下去喽,拆个柿子:
f[i]=a[i]+min{f[j]+(i^2+j^2-2ij-i+j)/2}
然后发现中间有个ij?完了,妈妈我不会了
显然的,这个玩意我们没有什么数据结构能维护,单调队列也很无能为力。
好了,到这里你肯定以为我就要推举出斜率优化了对不对?
那么事实上,我们先考虑下面的问题(好像无关紧要)
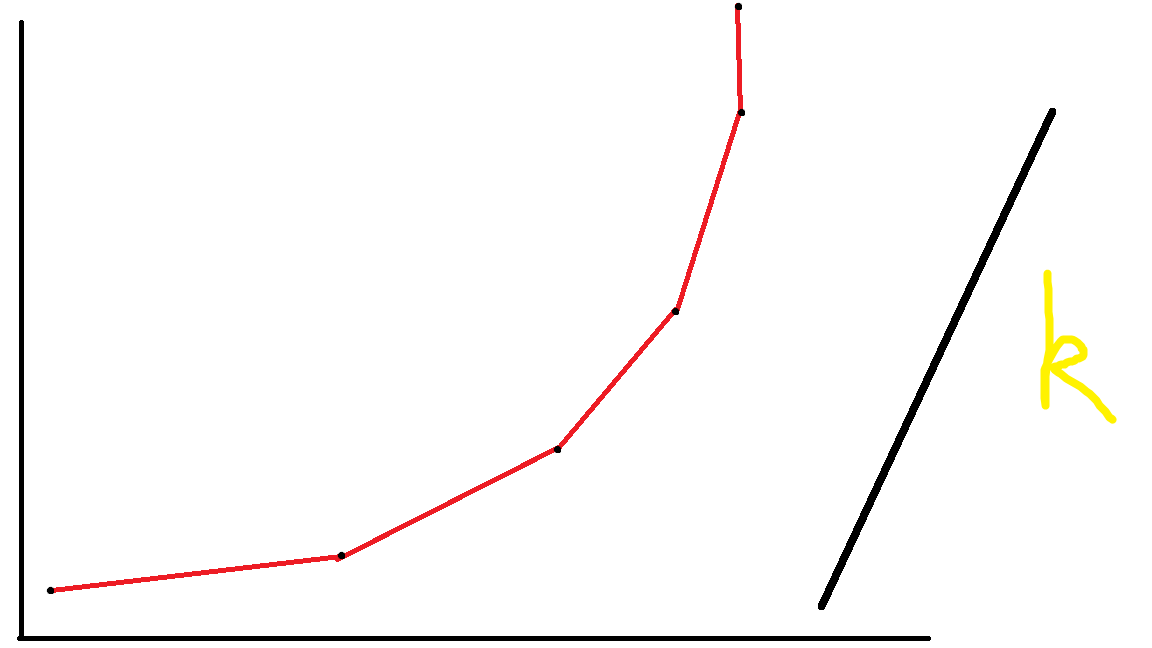
看的出来在坐标系上有许多个点(我们已知它们的坐标),它们的相邻两个之间的斜率是单调递增的(显然)然后我们有一个直线,其中k是它的斜率,问这个直线不断向左平移最先碰到哪个点。
那么同这个图我们看出第4个点是最先碰到的。为什么呢,发现第4个点与它前一个点的斜率小于k,与它后一个点的斜率大于k。然后这是巧合吗?显然不是。
至于证明,诶呀其实我也不太清楚,但是yy一下感觉总是对的,对吧QWQ
那么实现的话就更显然了,判断一下当前点与下一个点的斜率是否大于k,不是就下一个,是的话就是这个点啦。
然后再来一个
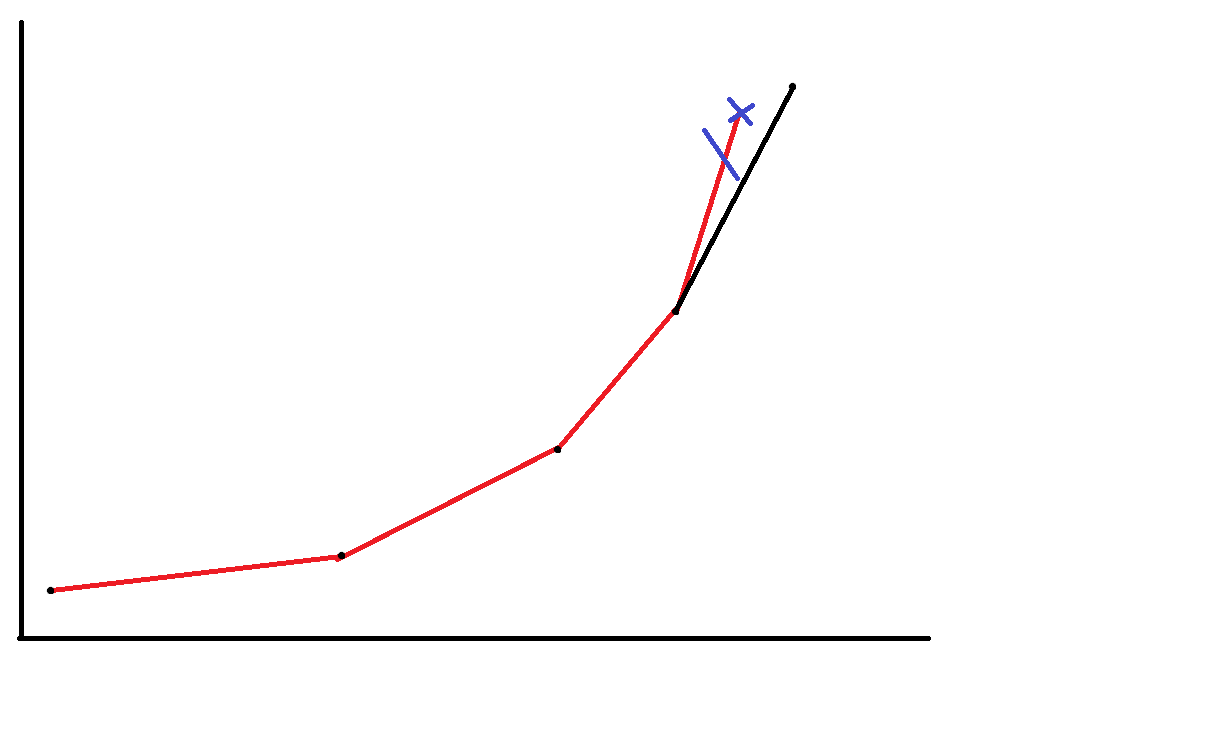
那么这一次我们要新加一个点,并且需要保持斜率单调递增(实际上这是个下凸包)那么怎么办呢?
就删点喽,我们从结尾开始,判断结尾与新加进来点的斜率是否小于结尾上个点与结尾的斜率,如果是,那么就把结尾删掉,然后一直删到大于等于。
好了,到了这里实际上已经讲述了斜率优化中去头去尾的操作(就是上面两个东东啊)
先说一嘴,斜率优化本质上还是用单调队列维护,只不过维护的条件是斜率之间比较,然后上面两个问题分别抽象了删头与删尾的过程(也就是维护单调队列的过程)
所以说zjy到这里好像你还是什么都没讲嘛(逃
实际上斜率优化就是把每个枚举的点转换成上面的坐标系中的点,然后对于维护就是上面两个问题(又是一句废话)
那么转换是说转换就转换的吗?
我们想想坐标系上的点需要什么?当然是横纵坐标啦!
于是乎,我们先来看看每个点的横纵坐标是啥。
f[i]=a[i]+min{f[j]+(i-j)*(i-j-1)/2}(0<=j<i)
dp是上面那玩意
然后:
f[i]=a[i]+min{f[j]+(i^2+j^2-2ij-i+j)/2}
我们把只关于i的移到另一边,min先去掉:
f[i]-a[i]-(i^2+i)/2=f[j]+(j^2+j-2ij)/2
额,好像还是看不出啥,把这个只关于i的去掉,然后只关于j的移到左边试试(额,实际上大家都知道柿子就是这么推的,但还是要有点气氛,有点感觉对吧,假装只是试试)
-f[j]-(j^2-j)/2=-2ij/2
负号不好看,取反:
f[j]-(j^2-j)/2=ij
二顺便除一下。
然后这个东西是个啥嘞?
回忆一下斜率表达式:kx=y
发现左边就如y一样,右边如kx一样
那么将计就计,我们设y=f[j]-(j^2-j)/2
那x呢?
我们发现i这个玩意十分的毒瘤(要不是因为它也不至于单调队列都无能为力)所以x就选j吧
那么k就是i喽。
然后通过上面的柿子,我们已经知道了每个点的坐标了吧,是不是就可以转换成上面两个问题呢?可能大家这个时候还是有点迷,但是没关系,我们先看看码吧。
#include<cstdio>
#include<cstring>
#include<iostream>
using namespace std;
int n,q[1000007];
long long a[1000007],f[1000007];
double xl(int i,int j){//这个函数是返回斜率滴,返回i与j两个点之间的斜率,由于i与j的横纵坐标都有了,所以就可以求啦。
return ((double)f[i]+(double)i*i/2+(double)i/2-((double)f[j]+(double)j*j/2+(double)j/2))/(i-j);//额这里无脑double了,然后/(i-j)之前一大坨就是纵坐标的差,(i-j)是横坐标的差,相除就是斜率
}
int main(){
scanf("%d",&n);
for(int i=1;i<=n;i++)
scanf("%d",&a[i]);
int h=1,t=1;//头与尾
q[1]=0;//0入队for(int i=1;i<=n;i++){
while(h<t&&xl(q[h],q[h+1])<=i) h++;//当我们还有点可以删的时候,并且此时第一个点与第二个点的斜率<=i,那么就删。
//首先为什么<=i呢,因为上面我们已经设k=i了啊,换句话说i就是斜率啊。上面的过程就是在原有的点中,找斜率为i的直线的最先遇到的点,而这个点也就是最优决策点。
//另外再说一下为什么斜率小于(等于时删不删其实无所谓的,因为该删时就一起删,不删时也就选一个)就直接删掉,由于i(也就是斜率)是不断递增的,所以这个点的斜率都小于i了,也必然小于后面的点的斜率。
f[i]
=f[q[h]]+a[i]+(i-q[h])*(i-q[h]-1)/2;//这时从队首转移就行啦
while(h<t&&xl(q[t-1],q[t])>=xl(q[t],i)) t--;//这个就是第二个操作了,由于这个时候f求出来了,那么i这个点的横纵坐标就都有了(j,f[j]-(j^2-j)/2),然后做第二个问题就ok啦
q[++t]=i; //i记得加入哦
}
printf("%lld\n", f[n]);
}
通过这个题似乎可以发现什么
其实所有的斜率优化都是一个套路,首先我们通过dp方程转移得到x,y,k(斜率)
其中k的用途就是来做第一个问题的,就是那个直线不断逼近。
然后x,y是我们得到坐标,由于这个坐标中有些奇奇怪怪的东西(实际上这个坐标就是奇奇怪怪,不对,斜率优化本身就很奇怪)如f数组,也就是我们的方程数组,所以当f[i]没求出来时,i的坐标我们也不知道,但是这个时候我们也不需要用,坐标是我们用来做第二个操作的。
所以对于以前的点,它只有坐标有用了,它的斜率只有在求它的时候才有用(为什么我一直强调这个呢,因为以前我就是不知道这个斜率是干嘛的,所以没搞懂)
大概流程如下:
1.设出动态转移方程
2.通过方程求得坐标以及斜率
3.for循环
4.对于点i,求i的斜率去逼近队列里的点,得到第一个符合条件的
5.此刻通过队首转移f[i]
6.得知f[i](也许还有其他东西,但是反正我们都知道了),也就是i的坐标得知了,然后把i插入队列里,若不满足凸包(单调性)就删队尾,一直删到满足,把i加入队尾。
注意事项:
1.对于不同的题目,不同的方程,其坐标以及斜率是不一样的(显然),如本题就是i,其他题也许就是2i之类的。
2.对于每道题,我们要考虑其斜率的单调性如何,是单调递增还是单调递减,如本题就是递增。若是递减的话,对于删头尾的操作也有些不同。
好了,那么大概问题都说清楚了,但是还有个问题,就是说这个坐标以及斜率到底该怎么求呢???
这里就不推式子了,说一下规律(若有错误,欢迎指正)
1.在方程中,只关于i的或者什么都不关于的我们选择无视,因为这相当于常量,几何意义上属于截距。
2.然后剩下的只有跟j有关和与j和i都有关了。
3.把只与j有关移项
4.这时就发现与j有关的在一边(一坨加减法),与ij有关的(单项式,只有乘)
5.然后只与j有关的是纵坐标,与ij有关的中,i一类为斜率,j一类为横坐标,关于系数尽量归为斜率部分。
哦,还有一个忘说了,斜率有可能为负数,这时就求两点之间的斜率就需要反过来了(若还不理解就自行yy)
关于单调性
斜率优化其实也是单调性的思想,只不过单调的是斜率,对于每个题我们也要判断其斜率是否呈单调性(如一个大一个小一个又大就不合法)若不是的话就只能另寻良机了(我也不知道是什么啊QAQ)
关于时间复杂度
1到n遍历O(n),每个节点入队一次出队一次又是O(n),所以总复杂度就是O(n)+O(n)=O(n)(大家都知道啦)
来源:oschina
链接:https://my.oschina.net/u/4312036/blog/4496467