8-7 偏差方差平衡



用学生的姓名来预测成绩,就会偏差很大,特征不对


knn对数据很敏感,一旦离它近的数据不合理或有问题则结果就不对,高度于依赖于样本数据

knn当使用所有样本时,即就是看哪个多就是哪个,则偏差最大,方差最小

机器学习的主要挑战,来自于方差,这是从算法的角度来说。
但对问题本身而言就不一定了,因为问题可能就很复杂,我们对其理解很肤浅。

方差可能就是学习了数据样本的噪音导致的
深度学习数据规模要足够多才可能有好的效果
8-8 模型泛化与岭回归08-Model-Regularization-and-Ridge-Regression

多项式回归过拟合的情况,有一些系数会很大,模型正则化就是限制其不要太大
很显然一些参数超级大

要考虑theta也尽可能的小,不需要theta0,它是截距,决定线的高低
限制theta的大小
alpha是新超参数,表示theta占的比重,如alpha为零则没有theta,如果为无穷大,则theta尽量小才能使目标尽可能小
这种方法又称为岭回归


from sklearn.pipeline import Pipeline
from sklearn.preprocessing import PolynomialFeatures
from sklearn.preprocessing import StandardScaler
from sklearn.linear_model import LinearRegression
def PolynomialRegression(degree):
return Pipeline([
("poly", PolynomialFeatures(degree=degree)),
("std_scaler", StandardScaler()),
("lin_reg", LinearRegression())
])
from sklearn.model_selection import train_test_split
np.random.seed(666)
X_train, X_test, y_train, y_test = train_test_split(X, y)
from sklearn.metrics import mean_squared_error
poly_reg = PolynomialRegression(degree=20)
poly_reg.fit(X_train, y_train)
y_poly_predict = poly_reg.predict(X_test)
mean_squared_error(y_test, y_poly_predict)
X_plot = np.linspace(-3, 3, 100).reshape(100, 1)
y_plot = poly_reg.predict(X_plot)
plt.scatter(x, y)
plt.plot(X_plot[:,0], y_plot, color='r')
plt.axis([-3, 3, 0, 6])
plt.show()
把训练的模型当成参数
def plot_model(model):
X_plot = np.linspace(-3, 3, 100).reshape(100, 1)
y_plot = model.predict(X_plot)
plt.scatter(x, y)
plt.plot(X_plot[:,0], y_plot, color='r')
plt.axis([-3, 3, 0, 6])
plt.show()
plot_model(poly_reg)使用岭回归

from sklearn.linear_model import Ridge
def RidgeRegression(degree, alpha):
return Pipeline([
("poly", PolynomialFeatures(degree=degree)),
("std_scaler", StandardScaler()),
("ridge_reg", Ridge(alpha=alpha))
])ridge1_reg = RidgeRegression(20, 0.0001)
ridge1_reg.fit(X_train, y_train)
y1_predict = ridge1_reg.predict(X_test)
mean_squared_error(y_test, y1_predict)
比之前的mse小的很多



8-9 LASSO


绝对值比ridge小平方的和要大,写程序初值可以小一点




from sklearn.linear_model import Lasso
def LassoRegression(degree, alpha):
return Pipeline([
("poly", PolynomialFeatures(degree=degree)),
("std_scaler", StandardScaler()),
("lasso_reg", Lasso(alpha=alpha))
])
lasso1_reg = LassoRegression(20, 0.01)
lasso1_reg.fit(X_train, y_train)
y1_predict = lasso1_reg.predict(X_test)
mean_squared_error(y_test, y1_predict)
比较Ridge和LASSO
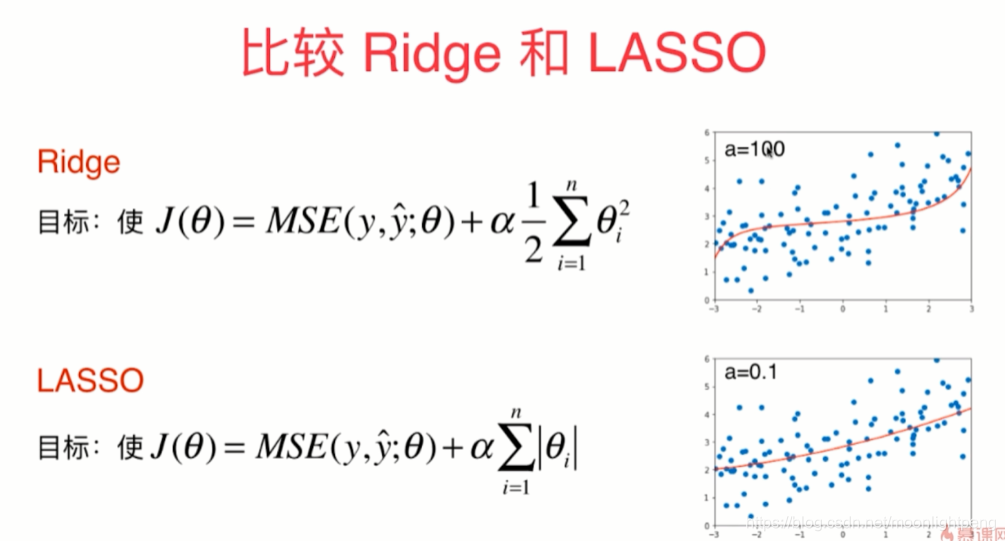
LASSO更倾向于直线,Ridge更倾向于曲线,
LASSO对应的theta有的为零,Selection Operator对应的特征无用

有时会把theta表示的有用的特征为零

导数为如上
在趋向于零的过程中每一步theta还有值,只是比较小,岭回归曲线向爬山

LASSO只能是直线
8-10 L1,L2和弹性网络


L1和L2正则

L2正则项或L2范数

L0正则
L0让非零theta的个数尽量小,实际很少用L0

离散
L1可以大量theta为零选择特征
弹性网 Elastic Net

结合L1和L2正则项,引入超参数r
实际上先使用ridge,其计算比较精准
如果参数太多,不具备特征选择的功能 让有些参数设为零
这时用弹性网,结合两者的优点精准和能特征选择
因为LASSO急于将有的参数化为零,这过程可能会产生错误
模型泛化,考试的练习题,在真正的考试中那些没见过的题效果好
来源:oschina
链接:https://my.oschina.net/u/4362740/blog/4306278