算法疑难(c++实现)---2、矩阵乘法

一、总结

一句话总结：

矩阵阵法就是按照矩阵相乘的规律，一步步来做的，也就是拿矩阵a的每一行乘以矩阵b的每一列，并且把矩阵a的每一行里面的每一个元素都和矩阵b里面每一列的每一个元素都一一相乘

Matrix multiply(Matrix a,Matrix b){
    Matrix ans;
    ans.row=a.row;
    ans.column=b.column;
    //遍历矩阵a的每一行
    for(int i=1;i<=a.row;i++){
        //遍历矩阵b的每一列
        for(int j=1;j<=b.column;j++){
            //把矩阵a的每一行里面的每一个元素都和矩阵b里面每一列的每一个元素都一一相乘
            for(int k=1;k<=a.column;k++){
                ans.v[i][j]+=a.v[i][k]*b.v[k][j];
            }
        }
    }
    return ans;
}

二、矩阵乘法

博客对应课程的视频位置：2、矩阵乘法
https://www.fanrenyi.com/video/30/281

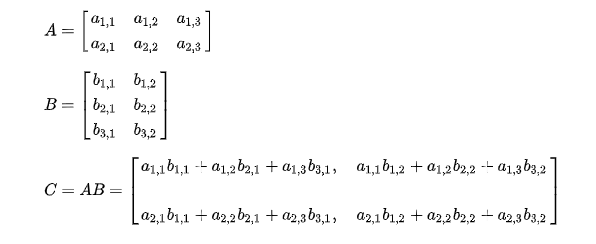
 1 /*
 2 
 3 矩阵的乘法在算法中有很多应用，
 4 比如直接考矩阵的乘法，比如用矩阵优化递推表达式等等
 5 
 6 
 7 矩阵a*矩阵b 要满足矩阵a的列等于矩阵b的行
 8 最后乘出来的矩阵的行为矩阵a的行
 9 列为矩阵b的列
10 
11 总结：
12 矩阵阵法就是按照矩阵相乘的规律，一步步来做的
13 也就是拿矩阵a的每一行乘以矩阵b的每一列，
14 并且把矩阵a的每一行里面的每一个元素都和矩阵b里面每一列的每一个元素都一一相乘
15 
16 
17 矩阵a
18 1 2 3 
19 4 5 6
20 
21 矩阵b
22 1 2
23 3 4
24 5 6
25 
26 
27 1*1+2*3+3*5
28 
29 */
30 
31 #include <iostream>
32 #include <cstring>
33 using namespace std;
34 
35 struct Matrix{
36     int row,column;
37     int v[5][5];
38     Matrix(){
39         memset(v,0,sizeof(v));
40     }
41 };
42 
43 Matrix multiply(Matrix a,Matrix b){
44     Matrix ans;
45     ans.row=a.row;
46     ans.column=b.column;
47     //遍历矩阵a的每一行
48     for(int i=1;i<=a.row;i++){
49         //遍历矩阵b的每一列
50         for(int j=1;j<=b.column;j++){
51             //把矩阵a的每一行里面的每一个元素都和矩阵b里面每一列的每一个元素都一一相乘
52             for(int k=1;k<=a.column;k++){
53                 ans.v[i][j]+=a.v[i][k]*b.v[k][j];
54             }
55         }
56     }
57     return ans;
58 }
59 
60 int main(){
61     Matrix a,b,ans;
62     a.row=2;a.column=3;
63     b.row=3;b.column=2;
64 
65     a.v[1][1]=1;a.v[1][2]=2;a.v[1][3]=3;
66     a.v[2][1]=4;a.v[2][2]=5;a.v[2][3]=6;
67 
68     b.v[1][1]=1;b.v[1][2]=2;
69     b.v[2][1]=3;b.v[2][2]=4;
70     b.v[3][1]=5;b.v[3][2]=6;
71 
72     ans=multiply(a,b);
73 
74     cout<<ans.v[1][1]<<endl;
75 
76     return 0;
77 }

来源：oschina

链接：https://my.oschina.net/u/4404863/blog/4306244

标签

c++

cstring