最小生成树 prim
问题引入:假设要在n个城市之间建立通信联络网,则连通n个城市需要n-1条路线,这是怎么样能在最节省经费的前提下建立这个通信网?
可以用联通网来表示n个城市,以及城市间的通信线路。其中顶点代表城市,边代表城市间线路,边的权值表示相应代价。n个顶点的联通网可以建立许多不同的生成树,其中要求的便是代价和最小的生成树。也称最小生成树。
构建生成树的算法多数利用了最小生成树的MST性质:
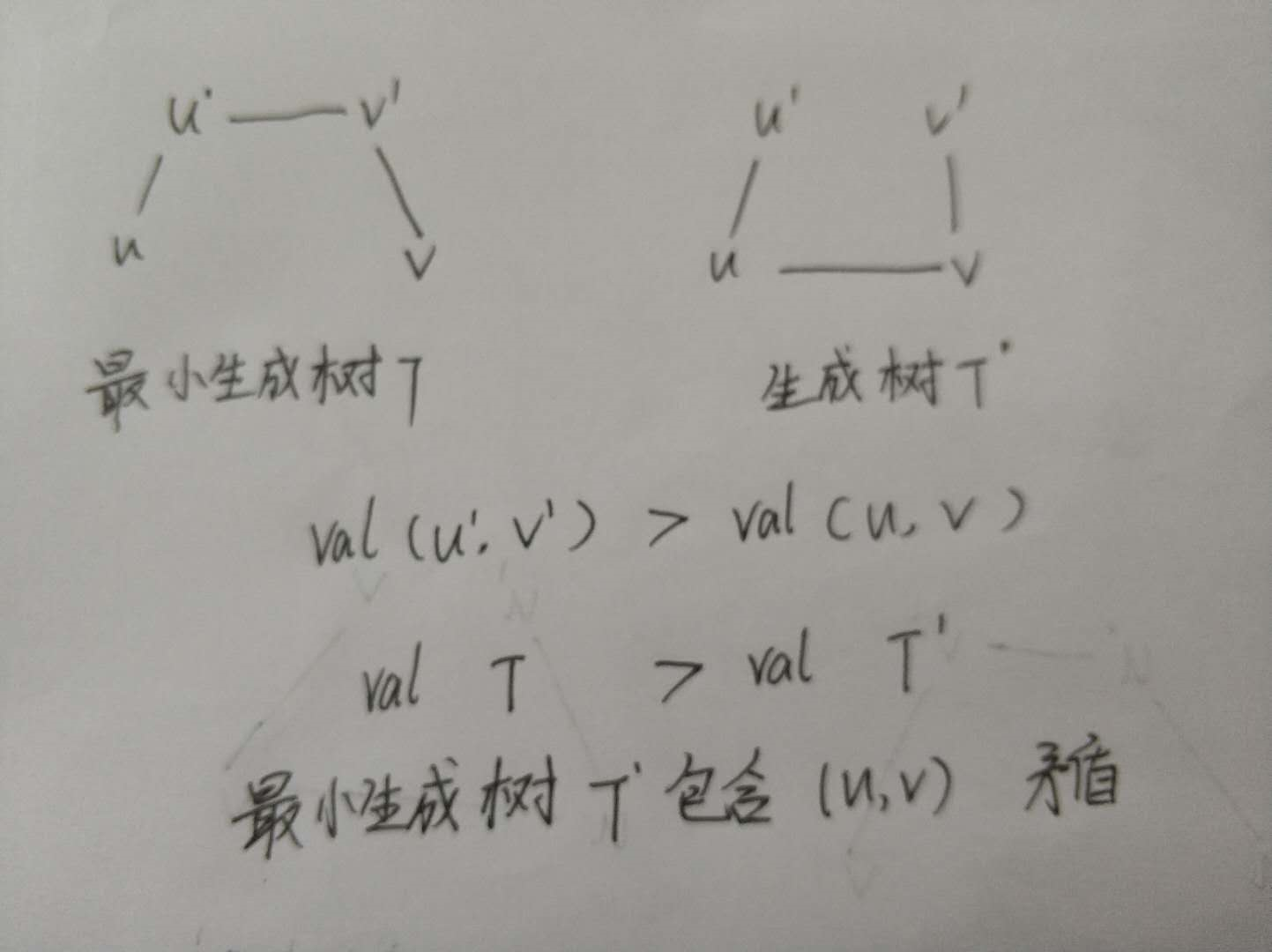
假设N=(V,E)是一个联通网,U是顶点集V的一个非空子集。若(u,v)是一条具有最小权值的边,其中u∈U,v∈V-U,则必定存在一颗包含边(u,v)的最小生成树
反证法:假设N的任何最小生成树都不包含(u,v),设T是联通网上的一颗最小生成树,当将边(u,v)加入T中,由生成树的定义,T中必定包含(u,v)的回路,由于T是生成树,则T上必存在另一条边(u`,v`),其中u`∈U,v`∈V-U,且u和u`之间,v和v`之间均有路径相通。删去边(u`,v`),便可消除上述回路,同时得到另一颗生成树T`,因为(u,v)的权值不高于(u`,v`),则T`的权值不高于T,T`是包含(u,v)的一颗最小生成树,由此和假设矛盾。
Prim算法
步骤:
假设存在N=(V,E)是联通网。
1、将N分成两个集合 S={u0} T={V-S} TE是N最小生成树边的集合
2、在所有的u∈S,v∈T的边(u,v)中找到一条权值最小的边(u0,v0)并入集合(u0,v0)并入集合TE,点v0并入S中
3、重复步骤2,直到S=V为止
此时TE中的必定有n-1条边,则T=(V,TE)是n的最小生成树
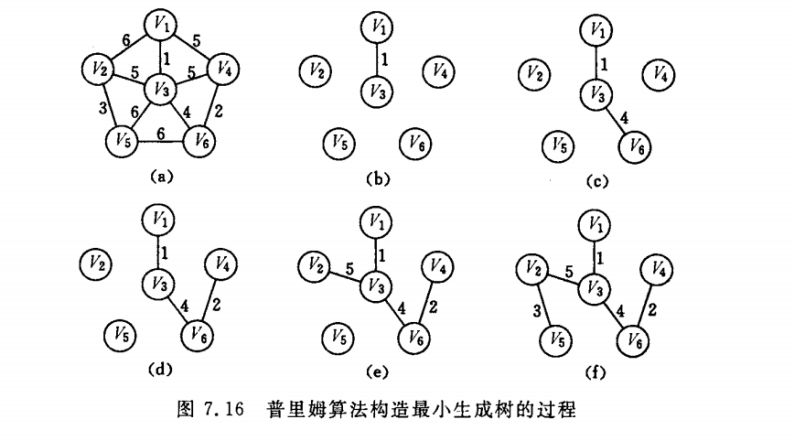
代码实现:以模板题为例(POJ - 1287 B - Networking)
//邻接矩阵存储图
#include<iostream>
#include<cstdio>
#include<cstring>
using namespace std;
const int MAX=60;
const int INF=0x3f3f3f3f;
int n,m,a,b,len;
int map[MAX][MAX]; //邻接矩阵存图
int dist[MAX]; //记录(u,v)的距离大小,其中u∈S, v∈T
bool vis[MAX]; //记录点是否已经在集合S中
int prim()
{
for(int i=1;i<=n;i++) //初始化
{
dist[i]=INF;
vis[i]=false;
}
dist[1]=0; //从点1开始生成最小生成树
int min,pos,ans=0;
for(int i=1;i<=n;i++)
{
min=INF;
for(int j=1;j<=n;j++) //找到(u,v)的最小值(u0,v0) 该边一定是最小生成树中的一条边
{
if(!vis[j]&&min>dist[j])
{
min=dist[j];
pos=j;
}
}
ans+=min; //加入生成树
vis[pos]=true; //将点 v0加入S集合中
for(int j=1;j<=n;j++)
{
if(!vis[j]&&dist[j]>map[pos][j]) //更新dist,看新集合S中是否存(u,v)更小的值,并取代
dist[j]=map[pos][j];
}
}
return ans;
}
int main()
{
while(1)
{
scanf("%d",&n); //顶点数
if(n==0)break;
scanf("%d",&m); //边数
for(int i=1;i<=n;i++) //初始化
for(int j=1;j<=n;j++)
map[i][j]=INF;
while(m--)
{
scanf("%d%d%d",&a,&b,&len);
if(map[a][b]>len)
map[a][b]=map[b][a]=len;
}
int ans=prim();
printf("%d\n",ans);
}
return 0;
}算法分析
算法中有两个循环,一个初始化循环,第二个循环包含两个内循环:1、在dist中寻找最小值 2、重新选择具有最小权值的边
prim算法的时间复杂度为O(n2),与图的边数无关,适用于求稠密图(点少边多)的最小生成树。
prim堆优化
根据上面的分析可以知道prim花费时间在dist中寻找边的最小值,和更新最小权值边,外层的n次是不可避免的,因为需要将n个点都加入最小生成数中。因此能够优化的地方
是寻找最小边的值。这里我们可以用一个优先队列(小根堆)来维护(u,v)抵达生成树边的值,每次取出队列最前且合法的边加到生成树中就可以,不合法的在过程中丢弃。
代码实现
#include<iostream>
#include<cstdio>
#include<cstring>
#include<queue>
using namespace std;
const int MAX=60;
const int MAXN=30000;
const int INF=0x3f3f3f3f;
int head[MAX],cnt=0;
int a,b,len,n,m;
int dist[MAX];
bool vis[MAX];
struct Edge{
int next,to,val;
}Edge[MAXN];
inline void add(int u,int v,int w)
{
Edge[cnt].to=v;
Edge[cnt].val=w;
Edge[cnt].next=head[u];
head[u]=cnt++;
}
struct node{
int pos,dist;
node(){}
node(int p,int d)
{
dist=d;pos=p;
}
bool operator < (const node &rhs)const //重载< 变成小根堆
{
return dist>rhs.dist;
}
};
int prim()
{
priority_queue<node>que;
memset(vis,false,sizeof(vis)); //初始化
for(int i=head[1];i!=-1;i=Edge[i].next) //将第一个点相连的边加入优先队列中
que.push(node(Edge[i].to,Edge[i].val));
vis[1]=true; //第一个点在集合S中
int num=n-1,ans=0;
while(num--)
{
node temp=que.top();que.pop(); //弹出小根堆第一个元素,这里第一个元素的dist最小
while(vis[temp.pos]) //但是并不一定可以用,若这个点已经在集合S中则不需要
{
temp=que.top();que.pop();
}
ans+=temp.dist; //将找到的边加入生成树中
vis[temp.pos]=true; //标记在S中的点(即加入生成树中的点)
for(int i=head[temp.pos];i!=-1;i=Edge[i].next) //更新距离
if(!vis[Edge[i].to])
que.push(node(Edge[i].to,Edge[i].val));
}
return ans;
}
int main()
{
while(1)
{
memset(head,-1,sizeof(head)),cnt=0; //初始化
scanf("%d",&n);
if(n==0)break;
scanf("%d",&m);
while(m--)
{
scanf("%d%d%d",&a,&b,&len);
add(a,b,len);
add(b,a,len);
}
int ans=prim();
printf("%d\n",ans);
}
return 0;
}
QAQ这道题看起来并没有快很多,反而慢了,自己也不太清楚,先占坑吧,
如有错误和不足欢迎指出,谢谢大家~
参考:
《数据结构 c语言版》严蔚敏
https://www.cnblogs.com/yspworld/p/4546098.html来源:oschina
链接:https://my.oschina.net/u/4337432/blog/3863360