1. 归一化(Normalization)
归一化 (Resaling) 一般是将数据映射到指定的范围,用于去除不同维度放入量纲以及量纲单位。常见的映射范围有 [ 0, -1 ] 和 [ -1, 1],最常见的归一化方法就是 Min-Max 归一化:
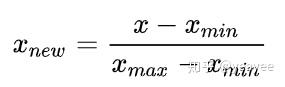
涉及距离度量、协方差计算时不能应用这种方法,因为这种线性等比例缩放无法消除量纲对方差、协方差的影响。
min_max_scaler = preprocessing.MinMaxScaler()
data_T_minmax = min_max_scaler.fit_transform(data.T)
data_minmax = data_T_minmax.T2. 标准化(Standardization)
最常见的标准化方法:Z-Score 标准化。
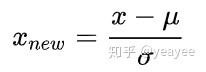
其中μ是样本均值,σ是样本数据的标准差。
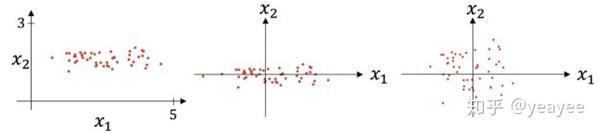
上图则是一个散点序列的标准化过程:原图 -> 减去均值 -> 除以标准差。
显而易见,变成了一个均值为 0 ,方差为 1 的分布,下图通过 Cost 函数让我们更好的理解标准化的作用。
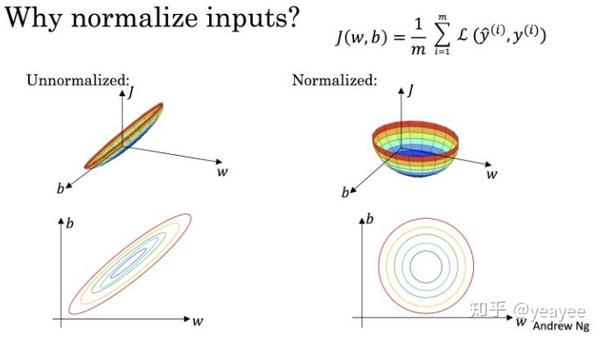
机器学习的目标无非就是不断优化损失函数,使其值最小。在上图中,J (w, b) 就是我们要优化的目标函数。
我们不难看出,标准化后可以更加容易地得出最优参数 w 和 b 以及计算出 J (w, b) 的最小值,从而达到加速收敛的效果。
注:上图来源于 Andrew Ng 的课程讲义
from sklearn import preprocessing
import pandas as pd
import numpy as np
mean=[4,3]
cov=[[2.0,5.],[1.,1.]]
x=np.random.multivariate_normal(mean,cov,7)
data=pd.DataFrame(x)
scaler = preprocessing.StandardScaler().fit(data.T) #对行做标准化处理
data_T_scale = scaler.transform(data.T)
data_scale = data_T_scale.transpose()3. 正则化(Regularization)
正则化主要用于避免过拟合的产生和减少网络误差。
正则化一般具有如下形式:
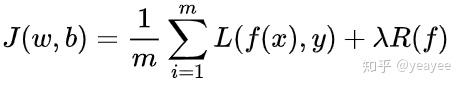
其中,第1项是经验风险,第2项是正则项,λ>=0 为调整两者之间关系的系数。
第1项是经验风险较小的模型可能较复杂(有多个非零参数),这时,第2项的模型度会较好。
常见的正则项有L1正则和L2正则,其中L2正则的控制过拟合的效果比L1正则的好。
正则化的作用是选择经验风险与模型复杂度同时较小的模型。
Lp范数:LpLp正则的L是指LpLp范数,其定义是:

在机器学习中,若使用了∣∣w∣∣p∣∣w∣∣p作为正则项,我们则说该机器学习引入了Lp正则项。
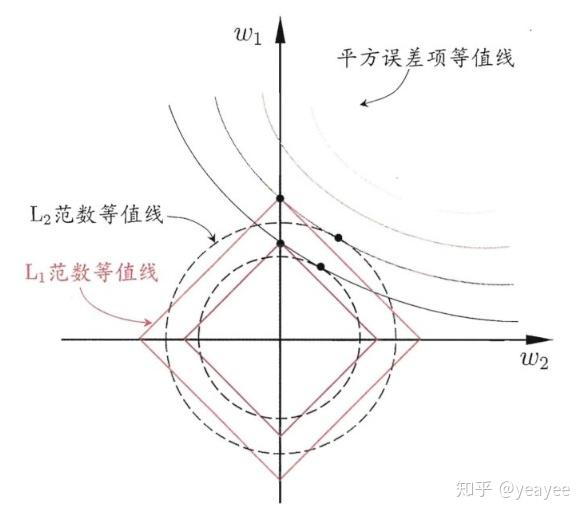
L1 正则 Lasso regularizer
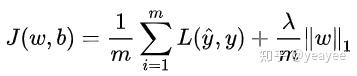
凸函数,不是处处可微
得到的是稀疏解(最优解常出现在顶点上,且顶点上的w只有很少的元素是非零的)
L2 正则 Ridge Regularizer / Weight Decay
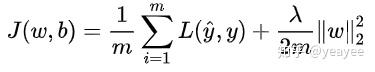
凸函数,处处可微;易于优化。
normalizer = preprocessing.Normalizer(copy=True, norm='l2').fit(data.T)
data_T_normalize=normalizer.transform(data.T) ————————————————
参考:
来源:oschina
链接:https://my.oschina.net/u/4391872/blog/4268889