八种常用排序算法（Java语言描述）

八种常用排序算法（Java语言描述）

TOC

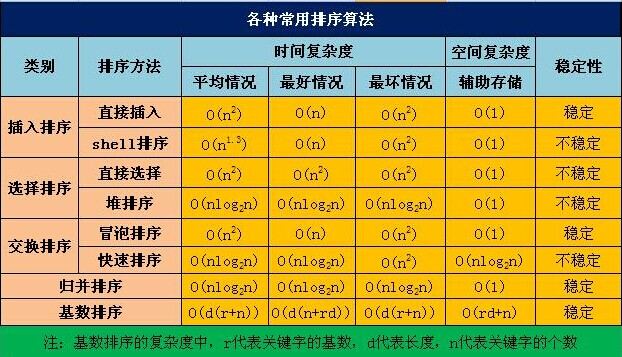
各种排序算法的时间、空间复杂度、稳定性对比分析

1、冒泡排序

冒泡排序（Bubble Sort），是一种计算机科学领域的较简单的排序算法。它重复地走访过要排序的数列，一次比较两个元素，如果他们的顺序错误就把他们交换过来。走访数列的工作是重复地进行直到没有再需要交换，也就是说该数列已经排序完成。这个算法的名字由来是因为越大的元素会经由交换慢慢“浮”到数列的顶端。

    /**
     * 冒泡排序
     * @param arr
     */
    public static void bubbleSort(int[] arr) {
        int temp;
        //比较总的轮数
        for (int i = 0; i < arr.length - 1; i++) {
            //每轮比较的次数
            for (int j = 0; j < arr.length - 1 - i; j++) {
                if (arr[j] > arr[j + 1]) {
                    temp = arr[j];
                    arr[j] = arr[j + 1];
                    arr[j + 1] = temp;
                }
            }
        }
    }

2、快速排序

快速排序（Quick Sort），又称划分交换排序，简称快排。它的基本思想：通过一趟排序将要排序的数据分割成独立的两部分，其中一部分的所有数据都比另一部分的所有数据小，然后再按照同样的方法对这两部分别进行快速排序，整个排序过程使用递归进行，最后整个数据都变成有序序列。

    /**
     * 快速排序
     * @param arr
     */
    public static void quickSort(int[] arr) {
        quickSortMain(arr, 0, arr.length - 1);
    }

    /**
     * 快排主方法
     * @param arr
     * @param start 头部指针起始位置
     * @param end 尾部指针起始位置
     */
    public static void quickSortMain(int[] arr,int start, int end) {
        //头部指针位置小于尾部指针位置进入递归
        if (start < end) {
            //定义标准元素
            int standard = arr[start];
            //定义始末指针
            int low = start;
            int high = end;
            //按照标准元素将原数组分成两部分
            while (low < high) {
                //先从尾部指针开始比较,比标准元素大,指针向前移动一位
                while (arr[high] >= standard && low < high) {
                    high--;
                }
                //若尾部指针的元素比标准数小,将该位置上的元素赋给头部指针位置
                arr[low] = arr[high];
                //头部指针判断,小于标准元素,指针向后移动一位
                while (arr[low] <= standard && low < high) {
                    low++;
                }
                //若头部指针比标准元素大,将其赋值给尾部指针位置
                arr[high] = arr[low];
            }
            //指针重合后,将标准元素赋值给重合位置
            arr[low] = standard;
            //将前后两组元素迭代再进行分组
            quickSortMain(arr,start,low);
            quickSortMain(arr,low + 1,end);
        }
    }

3、直接插入排序

插入排序（Insertion Sort）是一种简单直观的排序算法。它的工作原理是通过构建有序序列，对于未排序数据，在已排序序列中从后向前扫描，找到相应位置并插入。插入排序在实际上，通常采用in-place排序（即只需要O（1）的额外空间的排序），因此在从后向前扫描过程中，需要反复把已排序元素逐步向后挪位，为新元素提供插入空间。

    /**
     * 直接插入排序
     *
     * @param arr
     */
    public static void insertSort(int[] arr) {
        //遍历所有的数字
        for (int i = 1; i < arr.length; i++) {
            //如果当前的数字比前一个数字小
            if (arr[i] < arr[i - 1]) {
                //把当前遍历的数字存起来
                int temp = arr[i];
                int j;
                //遍历当前数字前面的所有数字
                for (j = i - 1; j >= 0 && temp < arr[j] ; j--) {
                    //把前一个数字赋值给后一个数字
                    arr[j + 1] = arr[j];
                }
                //把临时变量(外层for循环的当前元素)赋给不满足条件的后一个元素
                arr[j + 1] = temp;
            }
        }
    }

4、希尔排序

希尔排序（Shell Sort）是插入排序的一种，是直接排序算法的一种更高效的改进版本。希尔排序是非稳定的排序算法，它是把记录按下标的一定增量分组，对每组使用直接插入排序算法排序；随着增量逐步减少，每组包含的关键词越来越多，当增量减至1时，整个序列被分成一个有序序列。

    /**
     * 希尔排序
     *
     * @param arr
     */
    public static void shellSort(int[] arr) {
        //遍历所有的步长
        for (int d = arr.length / 2; d > 0; d /= 2) {
            for (int i = d; i < arr.length; i++) {
                //方法一(交换排序)
                /*for (int j = i - d; j >= 0; j-=d) {

                    if (arr[j] > arr[j + d]) {
                        int temp = arr[j];
                        arr[j] = arr[j + d];
                        arr[j + d] = temp;
                    }
                }*/
                //方法二(插入排序)
                int temp = arr[i];
                int j;
                for (j = i - d; j >= 0 && temp < arr[j]; j -= d) {
                    arr[j + d] = arr[j];
                }
                arr[j + d] = temp;
            }
        }
    }

5、简单选择排序

选择排序（Selection Sort）是一种简单直观的排序算法。它首先在未排序序列中找到最小（大）元素存放到排序序列的起始位置，然后再从剩余未排序元素中继续寻找最值元素，然后放到已排序序列的末尾。以此类推，直至所有元素均排序完毕。

    /**
     * 简单选择排序
     * @param arr
     */
    public static void selectSort(int[] arr) {
        int minIndex,temp;
        //遍历所有的数
        for (int i = 0; i < arr.length; i++) {
            minIndex = i;
            //将当前的数向后依次比较,并记录最小的数的下标
            for (int j = i + 1; j < arr.length; j++) {
                if (arr[minIndex] > arr[j]) {
                    minIndex = j;
                }
            }
            //如果当前的数和遍历后获取得最小下标的数不一样,交换
            if (i != minIndex) {
                temp = arr[minIndex];
                arr[minIndex] = arr[i];
                arr[i] = temp;
            }
        }
    }

6、堆排序

堆排序（Heapsort）是指利用堆这种数据结构所设计的一种排序算法。以升序为例，把数组转换成大顶堆，重复从大顶堆的根节点和最后一个节点交换，并移除最后一个节点，最后按取出顺序放入数组中（从数组最后一个位置放）。

    /**
     * 堆排序
     * @param arr
     */
    public static void heapSort(int[] arr) {
        //开始位置是最后一个非叶子节点,即最后一个节点的父节点
        int start = (arr.length-1)/2;
        //调整为大顶堆
        for (int i = start; i >= 0; i--) {
            maxHeap(arr,arr.length,i);
        }
        //先把数组中的第0个和堆中的最后一个数交换位置,再把前面的处理为大顶堆
        for (int i = arr.length - 1; i > 0; i--) {
            int temp = arr[0];
            arr[0] = arr[i];
            arr[i] = temp;
            maxHeap(arr,i,0);
        }
    }

    /**
     * 将完全二叉树处理为大顶堆
     * @param arr
     * @param size
     * @param index
     */
    public static void maxHeap(int[] arr, int size, int index) {
        //左子节点
        int leftNode = 2 * index + 1;
        //右子节点
        int rightNode = 2 * index + 2;
        int max = index;

        //和两个子节点分别对比,找出最大的节点
        if (leftNode < size && arr[leftNode] > arr[max]) {
            max = leftNode;
        }
        if (rightNode < size && arr[rightNode] > arr[max]) {
            max = rightNode;
        }
        //交换位置
        if (max != index) {
            int temp = arr[index];
            arr[index] = arr[max];
            arr[max] = temp;
            //交换位置后,可能会破坏之前排好的堆,所以,之前排好的堆需要重新调整
            maxHeap(arr, size, max);
        }
    }

7、归并排序

归并排序（Merge Sort），是创建在归并操作上的一种有效的排序算法。归并操作指的是将两个已经排好序的序列合并成一个序列的操作。

    /**
     * 归并（递归法）
     *
     * @param arr
     */
    public static void mergeSortMain(int[] arr,int low,int high) {
        //中间值
        int middle = (low + high)/2;
        //递归条件
        if (low < high) {
            //处理左边
            mergeSortMain(arr,low,middle);
            //处理右边
            mergeSortMain(arr,middle + 1,high);
            //并归
            merge(arr,low,middle,high);
        }
    }

    /**
     * @param arr
     * @param low 起始位置
     * @param middle 中间位置
     * @param high 末位置
     */
    public static void merge(int[] arr, int low, int middle, int high) {
        //用于存储并归后的临时数组
        int[] temp = new int[high - low + 1];
        //记录第一个数组中需要遍历的起始下标
        int i = low;
        //记录第二个数组中需要遍历的起始下标
        int j = middle + 1;
        //用于记录在临时数组中存放的下标
        int index = 0;
        //遍历比较两个数组中的数,取出小的数,放进临时数组中
        while (i <= middle && j <= high) {
            if (arr[i] <= arr[j]) {
                temp[index] = arr[i];
                i++;
            } else {
                temp[index] = arr[j];
                j++;
            }
            index++;
        }
        //处理多余的数据
        while (i <= middle) {
            temp[index] = arr[i];
            i++;
            index++;
        }
        while (j <= high) {
            temp[index] = arr[j];
            j++;
            index++;
        }
        //临时数组中的数据重新存入原数组
        for (int k = 0; k < temp.length; k++) {
            arr[low + k] = temp[k];
        }
    }

8、基数排序

基数排序（Radix Sort）是一种非比较型整数排序算法，其原理是将整数按位数切割成不同的数字，然后按每个位数分别比较。

    /**
     * 二维数组实现
     * @param arr
     */
    public static void radixSort(int[] arr) {
        //存储数组中最大的数字
        int max = Integer.MIN_VALUE;
        for (int i = 0; i < arr.length; i++) {
            if (arr[i] > max) {
                max = arr[i];
            }
        }
        //计算最大数字数几位数
        int maxLength = (max + "").length();
        //临时存储数据的数组
        int[][] temp = new int[10][arr.length];
        //记录在临时数组中数组对应的存放数量
        int[] counts = new int[10];
        //循环最大数字的长度次数
        for (int i = 0, j = 1; i < maxLength; i++, j *= 10) {
            //把每个数字分别计算余数
            for (int k = 0; k < arr.length; k++) {
                //计算
                int residue = arr[k] / j % 10;
                //将当前的数放进相应的数组中
                temp[residue][counts[residue]] = arr[k];
                //记录相应的数量
                counts[residue]++;
            }
            //取出数字
            int index = 0;
            for (int k = 0; k < counts.length; k++) {
                if (counts[k] != 0) {
                    for (int l = 0; l < counts[k]; l++) {
                        arr[index] = temp[k][l];
                        index ++;
                    }
                    //重置数量
                    counts[k] = 0;
                }
            }
        }

    }

    /**
     * 基数排序队列实现
     * @param arr
     */
    private static void radixQueueSort(int[] arr) {
        //存储数组中最大的数字
        int max = Integer.MIN_VALUE;
        for (int i = 0; i < arr.length; i++) {
            if (arr[i] > max) {
                max = arr[i];
            }
        }
        //计算最大数字数几位数
        int maxLength = (max + "").length();
        //临时存储数据的队列
        Queue<Integer>[] temp = new LinkedList[10];
        //初始化队列数组
        for (int i = 0; i < temp.length; i++) {
            temp[i] =  new LinkedList<>();
        }
        //循环最大数字的长度次数
        for (int i = 0, j = 1; i < maxLength; i++, j *= 10) {
            //把每个数字分别计算余数
            for (int k = 0; k < arr.length; k++) {
                //计算
                int residue = arr[k] / j % 10;
                //将当前的数放进相应的队列中
                temp[residue].add(new Integer(arr[k]));
            }
            //取出数字
            int index = 0;
            for (int k = 0; k < temp.length; k++) {
                while (!temp[k].isEmpty()) {
                    //删除并返回队列中第一个元素
                    arr[index] = temp[k].remove().intValue();
                    index++;
                }
            }
        }
    }

 

来源：oschina

链接：https://my.oschina.net/u/4264169/blog/4185820