1. 技术文章
  2. 可持久化线段树+主席树+动态主席树

可持久化线段树+主席树+动态主席树

由 北慕城南 提交于 2020-04-30 03:13:42

 

可持久化线段树

 

整体还是很容易理解的，网上的教程都挺不错，所以只简单介绍下

可持久化的原理在于，借用已经建过的线段树的一部分

比如，我们有一个数列$a=\{12,23,34,45,56,67,78,89\}$

而我们想要带修改的维护这个数列中$[L,R]$的区间和

建一颗正常的、维护$a_1$~$a_8$区间和的线段树就能解决了，这样就是不修改的情况

 

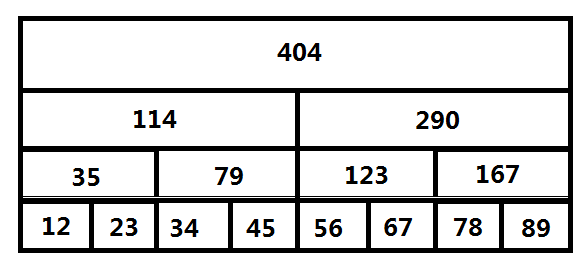
问题在于，如果想在这个的基础上维护历史版本，应当如何处理？

假设第一次修改，将$a_3$改为$90$

如果我们据此重新建立一颗线段树，可以发现，只有很少的节点跟初始的线段树有出入

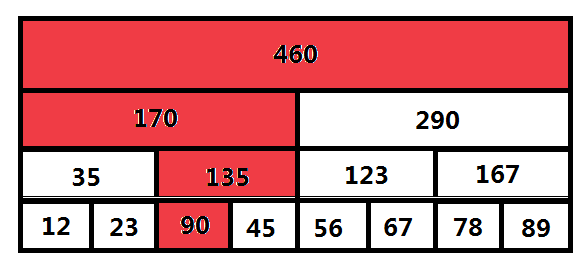
如果说的更加确切，有出入的节点为被修改点及其所有祖先

所以，我们建立一颗新的线段树，相当于向某个历史版本插入一条长度为logN的链

而对于这条链，每个节点的一个儿子一定指向一个没有出入的区间（即之前某个历史版本的节点）、另一个一定指向一个包含点修改的区间（新创建的节点），分开操作一下就行了

这样，$M$次操作时，整体的时空消耗是$O(N+MlogN)$

模板题：洛谷P3919

虽然是可持久化数组，但是稍微修改一下（把修改和查询换成区间）就是可持久化线段树了

（注释的是自己一开始犯的两个错误）

#include <cstdio>
#include <cstring>
#include <cmath>
#include <iostream>
using namespace std;

const int MAX=1000005;

int sz=1,cnt=0;

struct Node
{
    int val,l,r;
    Node()
    {
        val=l=r=0;
    }
}t[MAX*25];

int n,m;
int a[MAX];
int id[MAX];

void Build()
{
    id[1]=1;
    for(int i=1;i<sz;i++)
        t[i].l=(i<<1),t[i].r=(i<<1)+1;
    for(int i=1;i<=n;i++)
        t[i+sz-1].val=a[i];
    cnt=(sz<<1)-1;
}

inline void Modify(int k,int x,int l,int r,int y)
{
    if(l==r)
    {
        t[cnt].val=y;//#2: Mistake t[cnt] as t[k]
        return;
    }
    
    int mid=(l+r)>>1;
    if(x<=mid)
    {
        t[cnt].r=t[k].r;
        t[cnt].l=++cnt;
        Modify(t[k].l,x,l,mid,y);
    }
    else
    {
        t[cnt].l=t[k].l;
        t[cnt].r=++cnt;
        Modify(t[k].r,x,mid+1,r,y);
    }
}

inline int Query(int k,int x,int l,int r)
{
    if(l==r)
        return t[k].val;
    int mid=(l+r)>>1;
    return (x<=mid?Query(t[k].l,x,l,mid):Query(t[k].r,x,mid+1,r));
}

int main()
{
//    freopen("input.txt","r",stdin);
    scanf("%d%d",&n,&m);
    for(int i=1;i<=n;i++)
        scanf("%d",&a[i]);
    while(sz<n)
        sz<<=1;
    
    Build();
    id[0]=1;//#1: Missing initial situation
    
    for(int i=1;i<=m;i++)
    {
        int ver,op,x,y;
        scanf("%d%d",&ver,&op);
        id[i]=++cnt;
        
        if(op==1)
        {
            scanf("%d%d",&x,&y);
            Modify(id[ver],x,1,sz,y);
        }
        else
        {
            scanf("%d",&x);
            t[cnt]=t[id[ver]];
            printf("%d\n",Query(id[ver],x,1,sz));
        }
    }
    return 0;
}
View Code

 

 

重点还是真正的应用...比如

主席树

 

主席树又叫函数式线段树，可以解决的一种问题是 动态区间第$k$小

就是这道经典题：POJ 2104

网上有些博客在介绍的一开始讲的太本质了，导致反而有点难理解

***注意：线段树外的区间指的就是元素位置的区间，而线段树内的区间指的是元素离散化后的数值的区间***

我们先考虑，如何通过线段树，知道一个固定数列中第$k$小的数是多少【虽然这里的做法显得很笨，但是是主席树的简化版本】

我们可以将整个数列先离散化，然后对区间中的每一个数进行统计

例如：数列$a=\{10,20,30,20,50,10,60,40\}$，离散化后得到$b=\{1,2,3,2,5,1,6,4\}$

对于数列内每一个离散化后的数，我们建立一个基于数值的 区间和线段树 统计它的出现次数

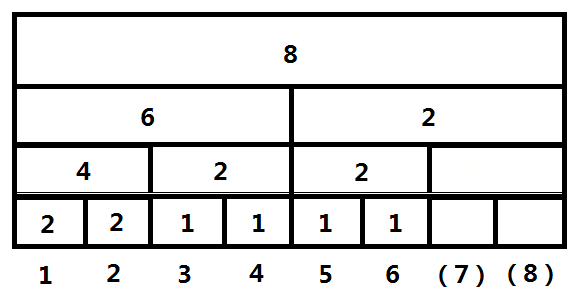
（$7$、$8$是用来占位的，可以无视）

这样，我们可以通过类似二分的思想找到第$k$小，而线段树的节点已经帮助我们将区间对半切分

假设我们想找区间第$7$小：

step 1: 区间$[1,4]$内的数一共出现了$6$次，所以我们可以直接进入另一区间$[5,8]$，并且找这个区间中的第$1$小

step 2: 区间$[5,6]$内的数一共出现了$2$次，所以$[5,8]$中的第$1$小一定也是$[5,6]$中的第$1$小

step 3: 区间$[5,5]$内的数一共出现了$1$次，所以$5$正是$[5,6]$中的第$1$小，即整个查询区间中的第$7$小

 

有了这样的铺垫，我们可以考虑引入可持久化的部分了

对于询问的某个区间$[L_i,R_i]$，我们就相当于在处理 只加入$L_i$到$R_i$的元素时候，像上面问题一样的区间第$k$小

所以为什么主席树叫做函数式线段树：我们可以通过前缀区间的相减来表示任意区间

用人话说，我们将离散化后的数列$b$的$n$个元素依次加入线段树中，进而产生$n+1$个历史版本（第$0$个历史版本是空线段树，其余依次为对$[1,1],[1,2],...,[1,n]$内元素的数值统计而成的线段树）

通过这个方法，我们就能表示区间$[L_i,R_i]$所产生的线段树了：对于每个节点，用第$R_i$版本的数值减去第$L_i-1$版本的数值（原理同用前缀和求区间和）

于是成功转化为了上面的问题

UPD：更新了一下代码

#include <cstdio>
#include <vector>
#include <cstring>
#include <algorithm>
using namespace std;

const int N=200005;

int root[N];

struct ChairmanTree
{
    int tot;
    int ls[N*20],rs[N*20],cnt[N*20];
    
    ChairmanTree()
    {
        tot=0;
        memset(root,0,sizeof(root));
        memset(ls,0,sizeof(ls));
        memset(rs,0,sizeof(rs));
        memset(cnt,0,sizeof(cnt));
    }
    
    void init()
    {
        memset(root,0,sizeof(root));
        for(int i=1;i<=tot;i++)
            ls[i]=rs[i]=cnt[i]=0;
        tot=0;
    }
    
    void pushup(int k)
    {
        cnt[k]=cnt[ls[k]]+cnt[rs[k]];
    }
    
    void add(int k,int x,int a,int b)
    {
        if(a==b)
        {
            cnt[++tot]=cnt[k]+1;
            return;
        }
        
        int cur=++tot,mid=(a+b)>>1;
        if(x<=mid)
        {
            ls[cur]=cur+1,rs[cur]=rs[k];
            add(ls[k],x,a,mid);
        }
        else
        {
            ls[cur]=ls[k],rs[cur]=cur+1;
            add(rs[k],x,mid+1,b);
        }
        pushup(cur);
    }
    
    //在第k个版本插入x 
    void insert(int k,int x,int a,int b)
    {
        root[k]=tot+1;
        add(root[k-1],x,a,b);
    }
    
    //在区间(l,r]中1~x的个数 
    //记得询问时l,r为root 
    int order(int l,int r,int x,int a,int b)
    {
        if(a==b)
            return cnt[r]-cnt[l];
        
        int mid=(a+b)>>1;
        if(x<=mid)
            return order(ls[l],ls[r],x,a,mid);
        else
            return cnt[ls[r]]-cnt[ls[l]]+order(rs[l],rs[r],x,mid+1,b);
    }
    
    //区间(l,r]中第k小的数（不存在返回-1） 
    //记得询问时l,r为root 
    int kth(int l,int r,int k,int a,int b)
    {
        if(k>cnt[r]-cnt[l])
            return -1;
        if(a==b)
            return a;
        
        int lp=cnt[ls[r]]-cnt[ls[l]],mid=(a+b)>>1;
        if(lp>=k)
            return kth(ls[l],ls[r],k,a,mid);
        else
            return kth(rs[l],rs[r],k-lp,mid+1,b);
    }
};

int n,m;
int a[N];
vector<int> v;

ChairmanTree t;

int main()
{
    scanf("%d%d",&n,&m);
    for(int i=1;i<=n;i++)
    {
        scanf("%d",&a[i]);
        v.push_back(a[i]);
    }
    
    sort(v.begin(),v.end());
    v.resize(unique(v.begin(),v.end())-v.begin());
    
    for(int i=1;i<=n;i++)
        t.insert(i,lower_bound(v.begin(),v.end(),a[i])-v.begin()+1,1,v.size());
    
    for(int i=1;i<=m;i++)
    {
        int x,y,k;
        scanf("%d%d%d",&x,&y,&k);
        printf("%d\n",v[t.kth(root[x-1],root[y],k,1,v.size())]);
    }
    return 0;
}
View Code

模板（多测记得调用init()，其他见注释）

#include <cstdio>
#include <cstring>
#include <algorithm>
using namespace std;

const int N=200005;

int root[N];

struct ChairmanTree
{
    int tot;
    int ls[N*20],rs[N*20],cnt[N*20];
    
    ChairmanTree()
    {
        tot=0;
        memset(root,0,sizeof(root));
        memset(ls,0,sizeof(ls));
        memset(rs,0,sizeof(rs));
        memset(cnt,0,sizeof(cnt));
    }
    
    void init()
    {
        memset(root,0,sizeof(root));
        for(int i=1;i<=tot;i++)
            ls[i]=rs[i]=cnt[i]=0;
        tot=0;
    }
    
    void pushup(int k)
    {
        cnt[k]=cnt[ls[k]]+cnt[rs[k]];
    }
    
    void add(int k,int x,int a,int b)
    {
        if(a==b)
        {
            cnt[++tot]=cnt[k]+1;
            return;
        }
        
        int cur=++tot,mid=(a+b)>>1;
        if(x<=mid)
        {
            ls[cur]=cur+1,rs[cur]=rs[k];
            add(ls[k],x,a,mid);
        }
        else
        {
            ls[cur]=ls[k],rs[cur]=cur+1;
            add(rs[k],x,mid+1,b);
        }
        pushup(cur);
    }
    
    //在第k个版本插入x 
    void insert(int k,int x,int a,int b)
    {
        root[k]=tot+1;
        add(root[k-1],x,a,b);
    }
    
    //在区间(l,r]中1~x的个数 
    //记得询问时l,r为root 
    int order(int l,int r,int x,int a,int b)
    {
        if(a==b)
            return cnt[r]-cnt[l];
        
        int mid=(a+b)>>1;
        if(x<=mid)
            return order(ls[l],ls[r],x,a,mid);
        else
            return cnt[ls[r]]-cnt[ls[l]]+order(rs[l],rs[r],x,mid+1,b);
    }
    
    //区间(l,r]中第k小的数（不存在返回-1） 
    //记得询问时l,r为root 
    int kth(int l,int r,int k,int a,int b)
    {
        if(k>cnt[r]-cnt[l])
            return -1;
        if(a==b)
            return a;
        
        int lp=cnt[ls[r]]-cnt[ls[l]],mid=(a+b)>>1;
        if(lp>=k)
            return kth(ls[l],ls[r],k,a,mid);
        else
            return kth(rs[l],rs[r],k-lp,mid+1,b);
    }
};
View Code

 

 

动态主席树

 

上面是简单的、在固定的数组上进行查询的主席树

如果在查询的同时支持对数组的点修改，不就更加NB了吗？

但是，这个功能的加入并不简单...又是看了几个博客强行理解了好久好久（有些讲解对新手不是很友好orz）

首先说明一下，动态主席树跟静态主席树在数据结构上已经有些差距了：动态主席树说到底是线段树套线段树（外层可以简化为树状数组），而静态主席树是重复利用的线段树，两者是有一定区别的

但是，动态主席树用到了和静态主席树类似的实现思想，就是维护前缀和（元素出现次数的前缀和）

在上面的静态主席树中，我们使用了可持久化线段树来维护元素，而每个前缀和是一颗线段树：虽然不同历史版本的线段树节点之间有交叉以重复利用，但每个历史版本都有唯一且独立的根节点

这就有点像我们求数列的区间和了：对于一个静态的数组$a_i$，我们先计算前缀和$pre_i=pre_{i-1}+a_i$，然后通过$pre_R-pre_{L-1}$来求$[L,R]$的区间和；但是如果想求一个带修改的数组的区间和，必须使用高级数据结构，例如线段树/树状数组

在这里也是相似的，只不过区间中的元素从简单的数字变成了记录数值出现次数的线段树了

于是，我们可以考虑 外层是线段树/树状数组、内层是记录数值出现次数的区间和线段树 这样的结构

  • 外层维护的是元素位置的区间：如果我们想查询$[L,R]$的第$k$小，我们首先找的是外层的对应$[1,R]$、$[1,L-1]$前缀和的几段区间（外层的节点，就是内层线段树的根节点）【外层的线段树的作用，是为了帮助我们找到位置区间对应的几颗内层线段树】
  • 内层维护的是数值的出现次数：每棵线段树表示，在根节点对应的外层区间中，每个数值出现的次数

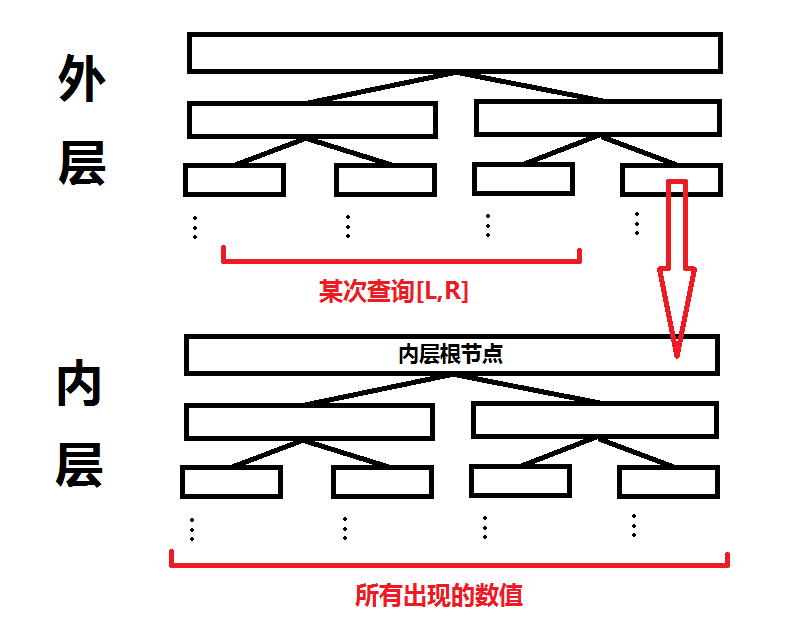
先不谈直观上是$O(N^2)$的空间消耗（默认已经以原数组为基础初始化过了）：后面会有办法解决这个问题；考虑一下使用这样结构的可行性

 

【修改】

如果将位置$p_i$的数$x$修改为$y$，我们在外层线段树发现$p_i$的位置一共被$logN$个区间（节点）包含；同时，以每个节点为根节点的线段树中，分别各有$logN$的节点的值被$x$、$y$影响

于是，对于外层每个包含$p_i$的节点，我们都应该在以其为根节点的内层线段树中将数值$x$的次数$+1$、将数值$y$的次数$-1$，并一直更新到内层线段树的根节点

这样，一次修改的复杂度是$O((logN)^2)$级别的

【查询】

如果外层是线段树，对于每次区间$[L,R]$的查询，我们都需要先在外层锁定仅包含区间$[L,R]$的内层根节点，这组节点最多有$logN$个

然后我们就可以转化为静态主席树的简单版本了，只不过这棵线段树的每个节点的数值 都是 以这组以节点为根的线段树 相同位置的节点 的数值之和（或者说，我们把这组线段树直接数值意义上的叠加在一起）

然后就是同上用类似二分的方法求区间第$k$小，就不再赘述了

如果外层是树状数组，对于每次查询，我们都需要先在外层分别锁定仅包含区间$[1,L-1]$、$[1,R]$的两组节点，每组节点最多有$logN$个

但是叠加成一颗线段树时，要减去$[1,L-1]$这组的叠加，加上$[1,R]$这组的叠加，后面还是一样的求区间第$k$小

这样，一次查询的复杂度也是$O((logN)^2)$级别的

 

现在我们回到一开始的问题：如何解决爆炸的空间？

如果把内层线段树的节点全部事先开好的话，就的确是$O(N^2)$的了；但事实上，我们一共能访问到内层线段树的多少节点呢？

每次修改（基于原始数组初始化相当于修改$N$次），同时间复杂度一样，是$(logN)^2$级别的

每次查询，仍然同时间复杂度一样，是$(logN)^2$级别的【但是查询并不会对任何内、外层节点带来修改，所以没有必要开点】

这样一来，我们真正能访问到的，一共也就$N\cdot (logN)^2$个内层线段树的节点；剩下来的，想都不用想，全是$0$，对于我们的查询并不会产生影响

所以，可以通过类似可持久化线段树的动态开点解决

 

模板题：洛谷P2617 （比原出处数据更强，甚至直接卡掉$O(N\cdot (logN)^3)$的线段树套平衡树）

说一下对我的坑点...其实动态主席树的实现在常数上是没多大区别的（线段树和树状数组差不多），我对着自己TLE的代码、抱着别人AC的代码，反反复复查了一天半都没找到个所以然

然后，发现我的离散化用的是$map$...在每次修改的时候也是直接用的map来找到离散化后的数（修改时一共调用了$3N$次$map$：初始、加、减各$N$次）

将离散化的互相对应关系用数组重新存了下，时间就直接降到了原来的一半，也就是说：$map$的常数约等于一个$logN$

细思极恐

不过在这里强烈推荐树状数组：在外层的各种定位可以直接通过加减$lowbit$的$for$循环完成，而线段树需要递归

（又注释了一些制杖bug）

#include <cstdio>
#include <cstring>
#include <cmath>
#include <cstdlib>
#include <map>
using namespace std;

const int MAX=100005;

int tot=1,sz=1;
int t[MAX*400],l[MAX*400],r[MAX*400];

int n,m;
int a[MAX];

inline int lowbit(int x)
{
    return x&(-x);
}

inline void Insert(int k,int p,int a,int b,int x)
{
    if(a==b)
    {
        t[k]+=x;
        return;
    }
    
    int mid=(a+b)>>1;
    if(p<=mid)
    {
        if(!l[k])
            l[k]=++tot;
        Insert(l[k],p,a,mid,x);
    }
    else
    {
        if(!r[k])
            r[k]=++tot;
        Insert(r[k],p,mid+1,b,x);
    }
    
    t[k]=t[l[k]]+t[r[k]];
}

inline void Add(int k,int p,int x)
{
    for(int i=k;i<=n;i+=lowbit(i))//#1: Need setting limits
        Insert(i,p,1,sz,x);
}

int idx;
map<int,int> mp;
int rev[MAX<<1];//#4: Forget to expand the size

void Build()
{
    while(tot<n)
        tot<<=1;
    for(int i=1;i<=n;i++)
        Add(i,a[i],1);
}

int lsz,rsz;
int vl[MAX],vr[MAX];

inline int Query(int a,int b,int x)
{
    if(a==b)
        return a;
    
    int mid=(a+b)>>1,sum=0;//#2: Counting left value
    for(int i=1;i<=lsz;i++)
        sum-=t[l[vl[i]]];
    for(int i=1;i<=rsz;i++)
        sum+=t[l[vr[i]]];
    
    if(sum>=x)//#3: Reverse the operator
    {
        for(int i=1;i<=lsz;i++)
            vl[i]=l[vl[i]];
        for(int i=1;i<=rsz;i++)
            vr[i]=l[vr[i]];
        return Query(a,mid,x);
    }
    else
    {
        for(int i=1;i<=lsz;i++)
            vl[i]=r[vl[i]];
        for(int i=1;i<=rsz;i++)
            vr[i]=r[vr[i]];
        return Query(mid+1,b,x-sum);
    }
}

inline void Locate(int x,int y)
{
    lsz=rsz=0;
    for(int i=x;i;i-=lowbit(i))
        vl[++lsz]=i;
    for(int i=y;i;i-=lowbit(i))
        vr[++rsz]=i;
}

char op[MAX];
int x[MAX],y[MAX],k[MAX];

int main()
{
//    freopen("input.txt","r",stdin);
    scanf("%d%d",&n,&m);
    for(int i=1;i<=n;i++)
        scanf("%d",&a[i]),mp[a[i]]=1;
    for(int i=1;i<=m;i++)
    {
        op[i]=getchar();
        while(op[i]!='C' && op[i]!='Q')
            op[i]=getchar();
        if(op[i]=='Q')
            scanf("%d%d%d",&x[i],&y[i],&k[i]);
        else
            scanf("%d%d",&x[i],&y[i]),mp[y[i]]=1;
    }
    
    for(map<int,int>::iterator it=mp.begin();it!=mp.end();it++)
        it->second=++idx,rev[idx]=it->first;
    while(sz<idx)
        sz<<=1;
    for(int i=1;i<=n;i++)
        a[i]=mp[a[i]];
    for(int i=1;i<=m;i++)
        if(op[i]=='C')
            y[i]=mp[y[i]];
    
    Build();
    
    for(int i=1;i<=m;i++)
        if(op[i]=='C')
        {
            Add(x[i],a[x[i]],-1);//#5: Mistake x[i] as i
            a[x[i]]=y[i];
            Add(x[i],a[x[i]],1);
        }
        else
        {
            Locate(x[i]-1,y[i]);
            printf("%d\n",rev[Query(1,sz,k[i])]);
        }
    return 0;
}
View Code

 

 

这样，可持久化线段树的概念就算是基本学完了（虽然动态主席树关联并没有那么大）←说的好像其他可持久化数据结构就会了一样

真正的难点是将可持久化的思想灵活运用到各种各样刁钻的题目当中

有时间的话再补些不错的题目上来orz

这算是我正式开始学习数据结构的入门吧...虽然都是大佬们随便玩的东西，我枯了

 

HDU 6703 （$array$，$2019CCPC$网络选拔赛）

这道题主要用到了两个转化的思想

第一个是，选$[1,r]$中不出现的数，可以转化为选$[r+1,n]$中出现的数（由于$a_i$为$1$到$n$的一个排列）

第二个是，将$a_i$加上$10^7$，相当于原来小于$n$的值对于任意$r$都能被选取，可以直接向后插入到主席树上

选取不小于$k$的最小值，可以通过先查询$k$的order（小于$k$的数的个数）、再查询第$order+1$小值完成

#include <cstdio>
#include <cstring>
#include <algorithm>
using namespace std;

const int N=200005;

int root[N];

struct ChairmanTree
{
    int tot;
    int ls[N*20],rs[N*20],cnt[N*20];
    
    ChairmanTree()
    {
        tot=0;
        memset(root,0,sizeof(root));
        memset(ls,0,sizeof(ls));
        memset(rs,0,sizeof(rs));
        memset(cnt,0,sizeof(cnt));
    }
    
    void init()
    {
        memset(root,0,sizeof(root));
        for(int i=1;i<=tot;i++)
            ls[i]=rs[i]=cnt[i]=0;
        tot=0;
    }
    
    void pushup(int k)
    {
        cnt[k]=cnt[ls[k]]+cnt[rs[k]];
    }
    
    void add(int k,int x,int a,int b)
    {
        if(a==b)
        {
            cnt[++tot]=cnt[k]+1;
            return;
        }
        
        int cur=++tot,mid=(a+b)>>1;
        if(x<=mid)
        {
            ls[cur]=cur+1,rs[cur]=rs[k];
            add(ls[k],x,a,mid);
        }
        else
        {
            ls[cur]=ls[k],rs[cur]=cur+1;
            add(rs[k],x,mid+1,b);
        }
        pushup(cur);
    }
    
    //在第k个版本插入x 
    void insert(int k,int x,int a,int b)
    {
        root[k]=tot+1;
        add(root[k-1],x,a,b);
    }
    
    //在区间(l,r]中1~x的个数 
    //记得询问时l,r为root 
    int order(int l,int r,int x,int a,int b)
    {
        if(a==b)
            return cnt[r]-cnt[l];
        
        int mid=(a+b)>>1;
        if(x<=mid)
            return order(ls[l],ls[r],x,a,mid);
        else
            return cnt[ls[r]]-cnt[ls[l]]+order(rs[l],rs[r],x,mid+1,b);
    }
    
    //区间(l,r]中第k小的数（不存在返回-1） 
    //记得询问时l,r为root 
    int kth(int l,int r,int k,int a,int b)
    {
        if(k>cnt[r]-cnt[l])
            return -1;
        if(a==b)
            return a;
        
        int lp=cnt[ls[r]]-cnt[ls[l]],mid=(a+b)>>1;
        if(lp>=k)
            return kth(ls[l],ls[r],k,a,mid);
        else
            return kth(rs[l],rs[r],k-lp,mid+1,b);
    }
};

int n,m;
int a[N];
ChairmanTree t;

int main()
{
    int T;
    scanf("%d",&T);
    while(T--)
    {
        t.init();
        
        scanf("%d%d",&n,&m);
        for(int i=1;i<=n;i++)
        {
            scanf("%d",&a[i]);
            t.insert(i,a[i],1,n);
        }
        
        int sz=n,ans=0;
        for(int i=1;i<=m;i++)
        {
            int op,x,y;
            scanf("%d%d",&op,&x);
            x^=ans;
            
            if(op==1)
            {
                if(a[x]<=n)
                {
                    t.insert(++sz,a[x],1,n);
                    a[x]+=n;
                }
            }
            else
            {
                scanf("%d",&y);
                y^=ans;
                
                int num=y-1?t.order(root[x],root[sz],y-1,1,n):0;
                
                ans=t.kth(root[x],root[sz],num+1,1,n);
                if(ans==-1)
                    ans=n+1;
                printf("%d\n",ans);
            }
        }
    }
    return 0;
}
View Code

 

（完）

标签
cstring
易学教程内所有资源均来自网络或用户发布的内容，如有违反法律规定的内容欢迎反馈！
该文章没有解决你所遇到的问题?点击提问,说说你的问题,让更多的人一起探讨吧!