等差数列，for循环，递归和尾递归的对比

生活中，如果1+2+3+4.....+100，大家基本上都会用等差数列计算，如果有人从1开始加，不是傻就是白X，那么程序中呢，是不是也是这样。今天无意中看到了尾递归，以前也写过，但是不知道这个专业名词，今天写一下对比下性能问题。

今天主要是看到了尾递归，所以联想到了这些，写下这篇文章，其中也把Benchmark (Nuget上的BenchmarkDotNet)的基准测试用了下，感觉比较好用，赞。Benchmark 需要在release下运行。

原则上所有的递归操作，都可以写成循环操作。尾递归是指，在函数返回的时候，调用自身本身，并且return语句不能包含表达式。这样编译器或者解释器就可以把尾递归做优化，试运行速度更快。

测试类

public class TestClass
{
    /// <summary>
    /// for循环
    /// </summary>
    /// <param name="n"></param>
    /// <param name="counter"></param>
    /// <returns></returns>
    public int TestFor(int n)
    {
        int s = 1;

        for (int i = 2; i < n + 1; i++)
        {
            s = s + i;
        }

        return s;
    }

    /// <summary>
    /// 等差数列
    /// </summary>
    /// <param name="n"></param>
    /// <param name="counter"></param>
    /// <returns></returns>
    public int TestForG(int n)
    {
        int s = (1 + n) * n / 2;

        return s;
    }

    /// <summary>
    /// 递归
    /// </summary>
    /// <param name="n"></param>
    /// <param name="counter"></param>
    /// <returns></returns>
    public int TestRec(int n)
    {
        if (n == 1) return 1;
        return n + TestRec(n - 1);
    }

    /// <summary>
    /// 尾递归
    /// </summary>
    /// <param name="n"></param>
    /// <param name="counter"></param>
    /// <returns></returns>
    public int TestTail(int n)
    {
        return TestTail(1, n);
    }

    public int TestTail(int sum, int n)
    {
        if (n == 1) return sum;
        sum = sum + n;
        return TestTail(sum, n - 1);
    }
}

View Code

基准测试

[SimpleJob(RuntimeMoniker.NetCoreApp30)]
[RPlotExporter]
public class TestClassForBenchmark
{
    private readonly TestClass testClass = new TestClass();

    [Params(100,500,1000,5000)]
    public int N;

    [Benchmark]
    public void TestFor()
    {
        testClass.TestFor(N);
    }

    [Benchmark]
    public void TestForG()
    {
        testClass.TestForG(N);
    }

    [Benchmark]
    public void TestRec()
    {
        testClass.TestRec(N);
    }

    [Benchmark]
    public void TestTail()
    {
        testClass.TestTail(N);
    }

}

View Code

Main程序调用

BenchmarkRunner.Run<TestClassForBenchmark>();

结果

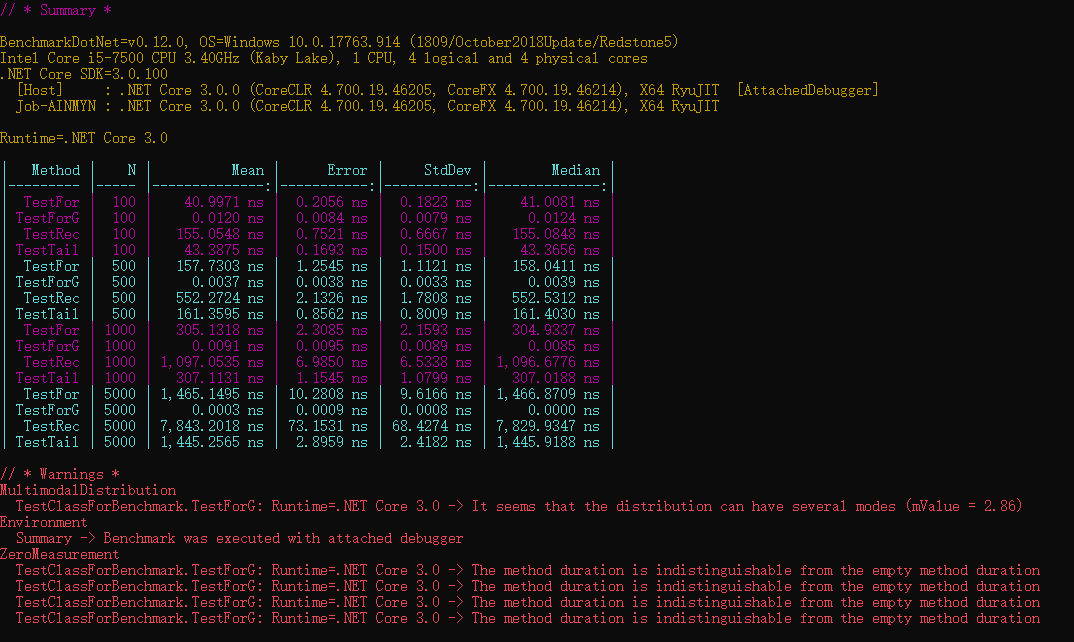
用Benchmark的基准测试发现，运行时间：等差 < for < 尾递归(接近for) < 递归，for的运行速度比递归快，但是递归结构比较清晰，容易理解。

发现TestForG有点问题，接下来自己简单测试

实际用Stopwatch测试

TestClass testClass = new TestClass();

Stopwatch stopSwitch = new Stopwatch();
int n = 5000;
stopSwitch.Start();
int sum = testClass.TestFor(n);
stopSwitch.Stop();
Console.WriteLine($"结果：{sum},TestFor时间:{stopSwitch.ElapsedTicks}");

stopSwitch.Start();
sum = testClass.TestForG(n);
stopSwitch.Stop();
Console.WriteLine($"结果：{sum},TestForG时间:{stopSwitch.ElapsedTicks}");

stopSwitch.Restart();
sum = testClass.TestRec(n);
stopSwitch.Stop();
Console.WriteLine($"结果：{sum},TestRec时间:{stopSwitch.ElapsedTicks}");

stopSwitch.Restart();
sum = testClass.TestTail(n);
stopSwitch.Stop();
Console.WriteLine($"结果：{sum},TestTail时间:{stopSwitch.ElapsedTicks}");

View Code

Stopwatch测试结果

1. 10次
结果：55,TestFor时间:2024
结果：55,TestForG时间:3799
结果：55,TestRec时间:1603
结果：55,TestTail时间:2371

2. 100
结果：5050,TestFor时间:1704
结果：5050,TestForG时间:2708
结果：5050,TestRec时间:1069
结果：5050,TestTail时间:1401
3. 500
结果：125250,TestFor时间:1794
结果：125250,TestForG时间:3096
结果：125250,TestRec时间:9398
结果：125250,TestTail时间:2332
4. 1000
结果：500500,TestFor时间:2080
结果：500500,TestForG时间:4147
结果：500500,TestRec时间:2003
结果：500500,TestTail时间:2540
5. 5000
结果：12502500,TestFor时间:1428
结果：12502500,TestForG时间:3982
结果：12502500,TestRec时间:6815
结果：12502500,TestTail时间:2799

结论

1. for的运行速度比递归快，但是递归结构比较清晰，容易理解。

2. 等差计算不一定比for循环快

斐波那契数列对比

/// <summary>
        /// 循环实现 counter:运行次数
        /// </summary>
        public long Fib(int n, ref int counter)
        {
            if (n < 1) return 0;
            long a = 1, b = 1;
            long temp;
            for (int i = 3; i <= n; i++)
            {
                counter++;
                temp = a;
                a = b;
                b = temp + b;
            }

            return b;
        }

        /// <summary>
        /// 递归实现
        /// </summary>
        public long FibRec(int n, ref int counter)
        {
            counter++;
            if (n < 1) return 0;
            if (n < 3) return 1;
            return FibRec(n - 1, ref counter) + FibRec(n - 2, ref counter);
        }

        /// <summary>
        /// 尾递归实现
        /// </summary>
        public long FibTailRec(int n, ref int counter)
        {
            if (n < 1) return 0;
            if (n < 3) return 1;
            return FibRec(1, 1, n, ref counter);
        }

        public long FibRec(long last, long prev, int n, ref int counter)
        {
            counter++;

            long temp = last + prev;
            if (n == 3) return temp;
            last = prev;
            prev = temp;

            return FibRec(last, prev, n - 1, ref counter);
        }

效果

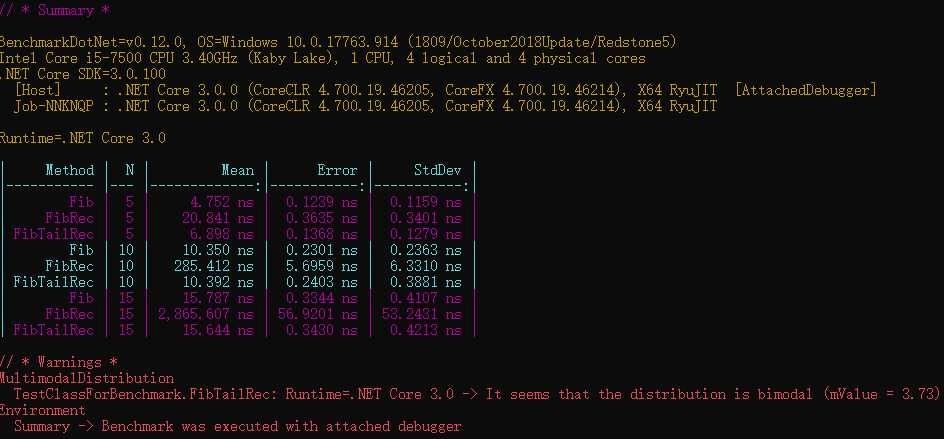
counter是运行的次数，斐波那契数列直接用递归，n=100都直接堆栈溢出。递归用的好了，思路清晰，用的不好的话，数据稍微大点就是深深的坑。用递归尽量优化为尾递归，也就是返回的时候调用自身，不要有表达式。

来源：oschina

链接：https://my.oschina.net/u/4373561/blog/3464659

标签

Benchmark

stopwatch